2010-01-06[n年前へ]
■重複部分がある1次元データを繋ぐメソッドをRubyのArrayクラスに追加する 
 重複部分がある1次元データを繋ぐメソッドを、RubyのArrayクラスに追加するコードを書いてみました。どういう機能かと言うと、たとえば、[1,2,3,4,5]というデータと[2,3,4,5,6]というデータがあったとしたら、それらの重複部分(同じものを示していると考えられる部分(すなわち[2,3,4,5])を重ね・重複しないように繋ぎ、[1, 2, 3, 4, 5, 6]というデータを出力するという機能です。
重複部分がある1次元データを繋ぐメソッドを、RubyのArrayクラスに追加するコードを書いてみました。どういう機能かと言うと、たとえば、[1,2,3,4,5]というデータと[2,3,4,5,6]というデータがあったとしたら、それらの重複部分(同じものを示していると考えられる部分(すなわち[2,3,4,5])を重ね・重複しないように繋ぎ、[1, 2, 3, 4, 5, 6]というデータを出力するという機能です。
だから、そのメソッド"connect"を使うと、たとえば、
require 'pp'
pp [1,2,3,4,5,6,"a","b",6].connect([6,"a","b",6,"3"])
a=[1,2,3,4,5].connect!([2,3,4,5,6])
pp a
なんていうコードを書くことができます。そして、その結果、
[1, 2, 3, 4, 5, 6, "a", "b", 6, "3"] [1, 2, 3, 4, 5, 6]という出力がされます。
注意事項は、a.connect(b)というコードを書くときには、a.length>=b.lengthである必要があります。また、1次元のArrayを念頭に書いてあります。
というわけで、適当に書いたArrayクラスの拡張コードは下記のような具合です。
class Array
def connect(another)
ret=nil
if self.length!=0
aLength=another.length
lastElements=self[self.length-aLength..self.length]
aNum=0
aLength.times do |num|
diff=0
(aLength-num).times do |i|
begin
diff+=1 if lastElements[i+num]!=another[i]
rescue
diff+=1
end
end
aNum=num
break if diff==0
end
ret=self+another[(aLength-aNum)..aLength]
else
ret=another
end
ret
end
def connect!(another)
self.replace(self.connect(another))
end
end
こんな機能を使う人はいないような気もしますが、自分の手習いも兼ねてここにコードをメモしておきます。上記コードの場合で言うと、connect!のような破壊的メソッドをを書くときには、"self=hoge"ではなく、"self.replace(hoge)"と書くのですね。
2010-03-22[n年前へ]
■「Mathematica からRuby on Railsのモデルを使う」のメモ 
 以前、「Mathematica からRuby on Railsのモデルを使う」でメモした、Mathematica User Conference 2009の資料、
Using Ruby on Rails Models with Mathematicaの内容を簡単にメモ書きしたので、ここに書いて(貼り付けて)おきます。
以前、「Mathematica からRuby on Railsのモデルを使う」でメモした、Mathematica User Conference 2009の資料、
Using Ruby on Rails Models with Mathematicaの内容を簡単にメモ書きしたので、ここに書いて(貼り付けて)おきます。
この資料は、大きく分けて次の4つの内容からなります。
- Rubyの紹介
- Ruby on Railsの紹介
- Mathematicaから直接SQLデータベースにアクセスする実践例 1つと、Ruby on RailsのActive RecordをMathematicaから使う実践例2つ
- MathematicaからRailsアプリで作成したWEB APIにアクセスする実践例1つ
 最後の「Mathematicaから直接SQLデータベースにアクセスする実践例 1つと、Ruby on RailsのActive RecordをMathematicaから使う実践例2つ、さらにrailsで作成したWEB APIにアクセスする実践例1つ」がどのようなものかを描くと、下の図のような具合です。1と3がactive Record(AR)を使った場合の処理で、2がMatheematicaから直接SQLサーバを叩く場合の例です。さらに、4番目の例は、RailsでWEB APIを作成する、という、まさに「疎」な結合の例です。この4番目の例は、…そもそも、MathematicaとRubyの両方を知っている人・そもそも作ることができる人しか楽しめないような気がしますから(人が一度に新しい事を知ることができるのは”ひとつ”まで、だと私は思っています)、「実際に役に立つ・新しい情報として楽しむことができる」のは3番目の例まで、かもしれません。
最後の「Mathematicaから直接SQLデータベースにアクセスする実践例 1つと、Ruby on RailsのActive RecordをMathematicaから使う実践例2つ、さらにrailsで作成したWEB APIにアクセスする実践例1つ」がどのようなものかを描くと、下の図のような具合です。1と3がactive Record(AR)を使った場合の処理で、2がMatheematicaから直接SQLサーバを叩く場合の例です。さらに、4番目の例は、RailsでWEB APIを作成する、という、まさに「疎」な結合の例です。この4番目の例は、…そもそも、MathematicaとRubyの両方を知っている人・そもそも作ることができる人しか楽しめないような気がしますから(人が一度に新しい事を知ることができるのは”ひとつ”まで、だと私は思っています)、「実際に役に立つ・新しい情報として楽しむことができる」のは3番目の例まで、かもしれません。
ちなみに、1の例は、RubyスクリプトからActive Recordを使い、中間ファイルを作り、そのファイルを介してMathematicaでActive recordモデルのデータを読み込む例で、3の例は中間ファイル無しに(けれど、原理的には1と同じやり方でSQLサーバ内のARモデルにアクセスするものです。

データを管理するのはSQLサーバで、(そのデータに対して)演算処理を行うのはMathematicという役割分担、そんな処理分担を使って作業してみたい人は、特に「そんなことをしてみたいけれど、よくやり方がわからない人」は一回眺めてみると良いと思います。とても、わかりやすい資料で、「技術紹介資料は、かくあるべし」とすら感じさせる資料です。とはいえ、この資料を楽しめるのは、MathematicaもRubyもRailsも、そのいずれをも少しはかじったことがある人に限られるのかもしれません。
こういう資料を眺めていると、この実践例は、MathematicaからRuby on Railsのactive Record モデルのデータを使う場合ですが、その逆に、Ruby on Railsのactive Record モデルにMathematicaの機能をメソッドとして実装した実践例も作りたくなりますね。
2018-06-17[n年前へ]
■「逆上がり」を「自然にできる」ための物理学的メソッド 
 胸ほどの高さにある鉄棒をつかみ、地面を蹴って鉄棒の上に回り込むのが「逆上がり」。慣れると簡単にできますが、一番最初は、なかなか回れず「運動なんかキライだ!」と感じてしまったりするものです。
胸ほどの高さにある鉄棒をつかみ、地面を蹴って鉄棒の上に回り込むのが「逆上がり」。慣れると簡単にできますが、一番最初は、なかなか回れず「運動なんかキライだ!」と感じてしまったりするものです。
よく「学校で勉強することなんて日常生活ではほぼ役に立たない」と言われたりしますが、たとえば「自然がどのような振る舞いを示すかを可能な限り簡易に説明する」のが、たとえば、物理だったりします。…というわけで、今日は、「逆上がり」を「自然にできる」ための物理学的メソッドを考えてみることにします。
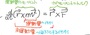
 まず、回転の運動方程式を思い浮かべれば(右図)、逆上がりを成功させるためには、まずはシンプルに地面を蹴る瞬間に回転のイキオイを最大化したくなります。
まず、回転の運動方程式を思い浮かべれば(右図)、逆上がりを成功させるためには、まずはシンプルに地面を蹴る瞬間に回転のイキオイを最大化したくなります。
運動量のモーメント(角運動量)が、大雑把には、回転原点(ここでは単純のために鉄棒位置としておきましょう)と蹴り上げる足が持つ運動量の外積であること、つまり、その大きさが「鉄棒から足先」と「足の運動量」からなる平行四辺形の面積を考えると、それを最大化するために必要なことは「足を蹴り上げる方向は鉛直上方向ではなくて、平行四辺形が直角形となる「斜め上」であることがわかります。つまり、必要なことは「上に高く飛ぶ」ではなく「足を前上方に蹴り上げる」ことだということになります。

もちろん、蹴り上げる際の「足の運動量」を最大化することも重要でしょう。ということは、たとえばサッカーでボールを蹴る「利き足」を「前上方向に蹴り上げられる側の足」にするということも効果的なはずです。つまり、サッカーでボールを蹴り上げるのと同じ動きで、利き足を上に蹴り上げて、その回転を行う運動モーメントを逆上がりの原動力とするわけです。
あるいは、それを言い換えれば、まずは「鉄棒の下に、非利き足で踏み込んだ上で、利き足を斜め前方上に蹴り上げる」というルーチーンが、自然に逆上がりを成功させるための動きとなるわけです。
大人の男性なら蹴り上げる時の足の速度は秒速15メートル(時速55キロメートル)程度です。この速度で人の体を単純化して計算してみると、上記の蹴り方をすれば、確かに逆上がりが成功する結果となります。
ちなみに、サッカー選手なら足を蹴り上げる速度は時速100キロメートルを越えたりします。 サッカーのワールドカップが開催されている今日この頃、サッカー選手の「逆上がり」を見てみたくなります。
2018-10-20[n年前へ]
■伊能忠敬メソッドで渋谷駅の地下大迷宮を可視化する!? 
 先週発売された「ソフトウェアデザイン 2018年11月号」に4ページ記事を書きました。題して「伊能忠敬メソッドで渋谷駅の地下大迷宮を可視化する!?」です。渋谷駅の地下内部構造の可視化とか、位置追跡とか構造物の階段角度とか、そんなことが好きな方は楽しんで頂ければ幸いです。
先週発売された「ソフトウェアデザイン 2018年11月号」に4ページ記事を書きました。題して「伊能忠敬メソッドで渋谷駅の地下大迷宮を可視化する!?」です。渋谷駅の地下内部構造の可視化とか、位置追跡とか構造物の階段角度とか、そんなことが好きな方は楽しんで頂ければ幸いです。
ちなみに、『(この記事を読めば)渋谷駅の地下が手に取るようにわかるのでしょうか?』というもらったコメントをもらいました。その答えは、『本記事で解説されているコードを使えば、3Dプリント可能な渋谷駅の可視化オブジェクトファイルも作ることができます。それはつまり、「 渋谷駅の地下を手に取ることができる」と言い換えることができます』