hirax.net::Keywords::「ベンフォードの法則」のブログ

■「大学入試問題」と「ベンフォードの法則」　

　大学入試問題の解答をYahoo!掲示板に質問した件が、ニュースになっています。今回の件であれば、状況的に、刑事事件として告訴無しでも送致するでしょうから、時間をおかずして通信業者は実行者にまつわる情報を保全すると共に・手順にのっとった開示を進め、時間をおかずに被疑者に対しての事情聴取が行われていくことでしょう。

　ところで、目の前に、数学の計算問題が置かれていたとして、しかも、その答えがちっともわからないとしたら、あなたなら一体どうすることでしょう？たとえば、それが、4択問題のマークシートなら、…どんなやり方で塗りつぶしを行うでしょう？

　hirax.net調べでは、「全部同じ番号を塗りつぶす」という答えが多いようです。4択問題のマークシートなら、全部同じ番号を塗りつぶせば25%が正解になるという理屈です。…行き当たりばったりでランダムマークシートを塗りつぶしたとしても、やはり25%の正解率を得ることができるような気がしますが、リサーチ結果を見るに、意外に「全部同じ番号を塗りつぶす」という意見が多いようです。

　世の中にあるものの多くは「対数的な分布」を示します。たとえば、人が得る収入額の分布・インターネットのアクセス数分布…といった数値はすべて、対数的な分布を描きます。そして。（少なくとも）そういった分布を示す数値がある時には、ベンフォードの法則が成り立ちます。それは「最初の桁が1である確率は30パーセントにもなる。そして、最初の桁に現れる数字は小さな数値ほど確率が高い」という法則です(２桁以降目の出現分布も導出され、応用されています)。だから、ある時期には、「試験で計算問題を解くことができなかった場合には、「（答えの）最初の桁の数値が１の選択肢を選ぶべし」という科学に裏付けられた（けれど情けない）解法が通用していました。

　ちなみに、正規分布のような確率分布をランダムに選んだ上で、その分布からさらにランダムに数値を選ぶなら、得られる数値の集合はベンフォードの法則に沿うということも証明されています。…つまり、私たちが出会う数値の多くはベンフォードの法則に沿う、というわけです。

　面白いことに、この「ベンフォードの法則」が見いだされたのは（少なくとも）19世紀のことでしたが、上記の証明がされたのは1995年でした。それは、つまり、それはつい最近に証明されたというわけです。実社会へ適用されてきたノウハウですが、そんなことに対する数学的な証明がようやく最近されている…というの、お少し面白いような感じがします。

■「雑誌の読者プレゼント」と「ベンフォードの法則」　

　「雑誌の読者プレゼント」でプレゼントが読者に送付されておらず、雑誌に「プレゼント当選者」として記されていた人たちの氏名（名字と名前）は、適当に作られた架空のものだったというニュースを見て、こんなことを考えました。

　名字や名前の比率がわかっていれば（さらには、県別年齢別のそういった比率などがわかっていれば）、雑誌に記されている「プレゼント当選者」たちの名前が統計的に見て「自然であるか、それとも不自然であるか」がわかりそうです。

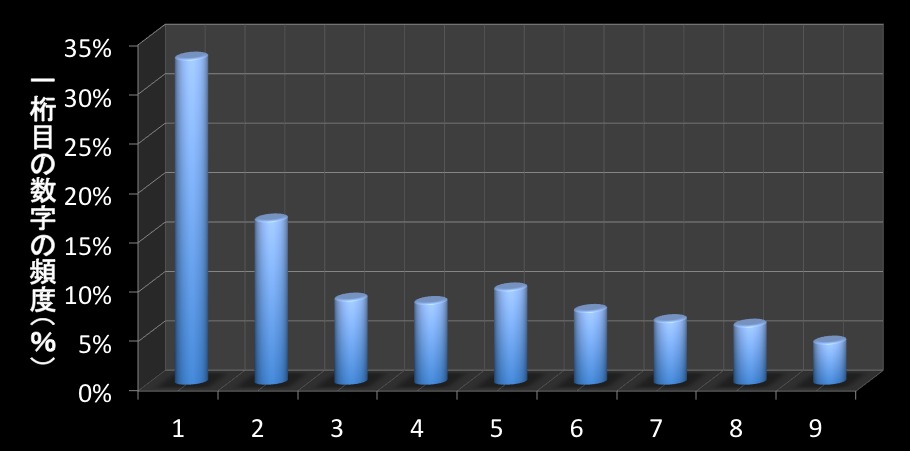　世の中にある多くの数字に対して「最初の桁が1である確率は30パーセントにもなる。さらに、最初の桁に現れる数字は小さな数値ほど確率が高い」というベンフォードの法則が成り立ちます（参考：「大学入試問題」と「ベンフォードの法則」）。たとえば、右のグラフは「2011年にhirax.netからAmazon広告経由で販売された商品データ一覧」を使って、「商品の値段の一桁目の数字は何か？」を調べてみた結果です「一桁目の数字の３割は”１”である」という「ベンフォードの法則」にほぼ沿っていることがわかります。逆に言えば、こんな風に数字の統計データを眺めてみた時に、「ベンフォードの法則」に沿っていなければ、「あれ？何だか不自然だな…何か隠れた理由があるんだな」ということに気がつくことができるわけです。

　雑誌の読者プレゼント当選者たちの名前を「統計的に自然であるか・自然でないか」を自動チェックしたら、一体どんな風になるのでしょうか。たとえば、鈴木・佐藤・田中…といった名字を持つ「当選者」の比率は、現実の比率に沿ったものなのでしょうか。あるいは、名前の比率は自然なのでしょうか？…ちょっと調べてみたくなりますね。

　もしかしたら、将来の電脳世界では、電脳世界中にあるリストデータたちに対して、そういったリストの中身が「自然か不自然か」を判断するパトロール・ロボットが存在し、電脳世界を日夜取り締まりしていたりするかもしれません。