hirax.net::Keywords::「雲」のブログ

■夕暮に輝く「夏雲の尻尾（シッポ）」　

　湿気て暑い夕暮れ時、「シッポを垂らした雲」たちが空に浮かんでいました。日没を過ぎて、地平線の無効から夕日が雲の尻尾を赤く照らしています。

　雲から伸びるシッポ（尻尾）は「尾流雲」と呼ばれ、雲から降り落ちる雪や雨です （参考：「雲のシッポ」の中に入ってみた。, 雲のシッポは「雲からこぼれ落ちる雪」）。 雲からこぼれ落ちていく雪や雨が、地上に届く前に空気中で蒸発し、シッポのように見えるのです。

　まだまだ蒸し暑い真夏日の夕方、空に浮かぶ雲が垂らす赤白い尻尾は、それは「雨」なんだろうか？それとも「雪」なんだろうか？と考え・想像すると、何だか少し涼しくなってくる…わけもなく、昔ながらの蒸し暑い「日本の夏」を感じる夏の夕暮れ、です。

■空に浮かぶ雲の大きさから、雲の高さや地球の大きさを推定する方法　

　青空に浮かぶ白い雲を眺めながら、こんなことを訊かれたことがある。

「たとえば、南の空に浮かぶ、天頂からちょうど４０度くらいの角度の雲までの距離や高さを、眺めた景色から計算することができる？」

　雲の高さやその雲までの距離、それらを一体どうやったら知ることができる？という質問だ。もちろん、気象に詳しい人なら、たとえば「あれはひつじ雲で、近くの山の高さと比較すると、多分高さは３千メートルくらいだろう」という具合で、雲の種類や見え方から、雲の高さを知ることができるかもしれない。そして、雲の高さがわかってしまえば、雲までの距離を計算するための式は幾何的に導出することができる。それは、雲の高さをｒ、天頂からの角度をαとし、地球の半径6371ｋｍをRとしたこんな式だ。

　実際のところ、雲の高さや距離は、どちらか片方がわかってしまえば、もう片方は自動的に求まる性質のものだ。前述の「雲までの距離」を計算するための式は、雲の高さr、雲の天頂からの角度α、地球の半径Rという３つのパラメータを用いたものだから、天頂角度α、地球半径Rがわかっている限りは、雲の高さか雲間での距離のどちらか片方がわかってしまえば、残りひとつの未知数は単純に計算することができる。たとえば、雲の高さを地上から２０００ｍに固定すると、雲が見える方向（天頂からの角度）に応じた雲までの距離は、次のようなグラフとして描くことができる。

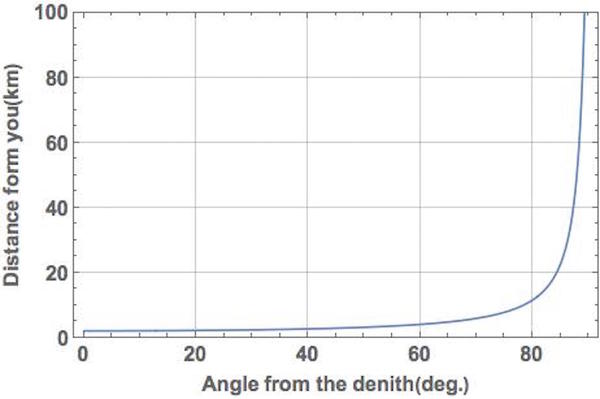
　けれど残念なことに、その時のぼくには、雲や気象に関する知識がほとんど無かったので、「一体どうすれば雲の高さや距離を知ることができるのだろう？」と考えながら、ただ黙っていた。

　目の前の景色から雲の高さと距離を知る方法を尋ねられてから何年も経った今日、バンコクの空に浮かぶ雲を眺めながら、こんな「空に浮かぶ雲の高さと距離を推定する方法」をふと思いついた。それは、こんな考え方だ。

　雨季から乾季を迎えたバンコクの青空には多くの「わた雲」が浮かんでいる。このわた雲たちはどれも同じ物理現象の結果生じたもので、いずれもとても安定な状態で空に浮かんでいるのだ。だとしたら、きっと似たような大きさをしていると考えるのが自然だろう。そしてまた、大気気象的には、どの雲の底面も地上からの高さはほぼ同じになっているはずだ。

　そして、雲の「天頂からの角度」と「見た目の大きさ」は、眺めた景色から知ることができる。だとすれば、雲までの距離は雲の見た目の大きさに（比例係数をｓとして）反比例しているという関係を使って、上述の式に、雲の「見た目の大きさと天頂からの角度」を既知（わかっている数値）として代入すれば、雲の高さｒと比例係数ｓを２未知数とした方程式ができあがる。それはつまり、距離が異なる２個以上の雲の大きさを観察して、その雲の大きさや場所を代入した連立方程式を解けば、雲の高さや距離がわかる、ということになる。

　ためしに、バンコクで眺めた雲の位置と大きさの関係をデジカメ撮影画像から算出して、散布図にしたのが下左図だ。天頂から離れた「遠い」雲ほど小さいという単純な関係だ。この雲の位置と大きさを観察した関係から、雲の高さｒと比例係数ｓを「手動で」フィッティングしてみると、たとえば、雲の（底面）高さが５００ｍの場合で、下右図のような対応となる。この数日が真実と近いのか・遠いのかはわからないけれど、こんな風に、原理的には、大きさが同じ雲の位置や大きさがどのように見えるかを調べてやれば、雲の高さや雲までの距離は知ることができる…かもしれない。

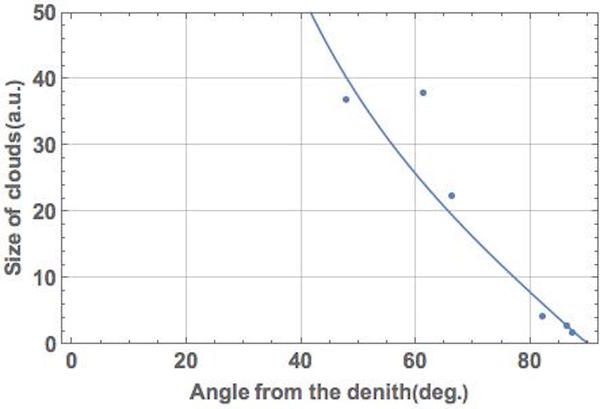
　…「原理的には」「かもしれない」と書いたのは、前述の式は、雲の高さｒを求めるには精度が低い式だからだ。式自体は「”地球の半径＋雲の高さ”を半径とする円」と「雲を見上げた視線の直線」の交点から導かれる方程式で、雲の高さが地球半径に比べて遙かに小さいために、精度良く雲の高さや雲間での距離を求めることは、おそらく難しいからだ。

　地球の半径に比べて雲の高さが遙かに小さいから、この方程式を使っても雲の高さを求められない？…だとしたら、頭上から地平線近くまで散らばる雲の大きさとこの連立方程式を使って地球半径を計算してみるのはどうだろう？この方程式は、雲の高さr、雲の天頂からの角度α、地球の半径Rという３つのパラメータを結びつけるものだから、たとえば「雲の天頂からの角度αは見たままに、わた雲の高さｒは気象の知識や周りの山などの比較から地上５００ｍとする」というように考えれば、あとは雲の大きさから地球半径Rを求めることができるかもしれない。

　ためしに、上に使ったデータで最小二乗フィッティングを行ってみると、地球半径R=約６万２千ｋｍという結果になった。教科書に載っている地球の半径約６千３百ｋｍと比べると、１０倍ほども大きい巨大な地球になってしまった。良い結果を得ることができたとは全く言えない。

　その理由は、地平線近くの遠い雲といっても、自分を中心にした数十ｋｍ程度の距離しかないので、その見え方から直径にして１万２千ｋｍもの地球の大きさを計算するにはとても無理があるからだ。

　けれど、青空に広がる雲を眺め、雲の位置や大きさがどんな風に見えるかを調べて、地球の大きさを求めてみることができるかもしれないと考えると、何だかとてもワクワクさせられる気がする。