■分数階微分に基づく画像特性を考えてみたい 
同じ年齢でも大違い
前回、分数階微分の謎 - 線形代数、分数階微分、シュレディンガー方程式の三題話- で分数階微分について調べた。例えば、0.7階微分といった、整数階でない微分である。今回はそれを使った応用を考えてみたい。
人間の視覚というものは明るいものは強く感じることができる。これは当たり前である。そして、それだけでなく、強さが変化している所にも(興味を)強く感じ取るようになっている。岡本安春氏の「Delphiでエンジョイプログラミング」によれば、そのような考えはLaming(1986)がdifferential coupling(差動結合)として発表しているらしい。
ということは、人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。とすれば、分数階微分を導入すれば面白い表現ができるかもしれない。
今回は、そういう考えのもとに分数階微分を用いて人間の画像特性について考えてみたい。
まずは、元画像を示す。元画像はガウス分布に基づいて作成されたものである。
 |  |
まずは、左の元画像を見て欲しい。どこに強い感じを受けるだろうか?白い部分はもちろんであるが、白と黒の境界部にも強い感じを受けるだろう。ギザギザになっているのはデータが少ないからなので、無視して欲しい。というわけで、人間の視覚画像特性は
- 画像強度
- 画像強度変化(画像強度の一階微分)
 元画像 |  |
 1/2階微分画像 |  |
 15/20階微分画像 |  |
 1階微分画像 | 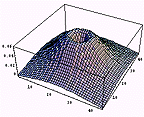 |
白地に黒画像バージョンも示しておく。紙の上の画像に慣れた人にはこちらの方が良いだろう。
 元画像 |
 1/2階微分画像 |
 15/20階微分画像 |
 1階微分画像 |
なお、今回の画像の作成は次のような手順で行っている。
- 1次元のガウス分布を作成する。
- 微分値が正であるような半分の領域を線対称に回転させ、2次元画像を作成する。
今回は
- 画像強度
- 画像強度変化(画像強度の一階微分)
- 電位
- 電界(電位の微分、といっても本来は電位が電界の積分か)
- 人口密度
- 人口密度変化(人口密度の微分)
さて、分数階微分を調べる中で、バナッハ空間についても調べた。調べ始めた時には、聞き覚えもなかったが、調べてみるとヒルベルト空間の導入で登場していた。きれいさっぱり忘れていたようである。
京大数学教室 徳永健一氏のWEB (http://www.kusm.kyoto-u.ac.jp/~kenichi/)
から辿れる「「年齢の本」数学者版」によれば
バナッハがバナッハ空間を提唱したのは30歳の時であるらしい。(http://www.kusm.kyoto-u.ac.jp/~kenichi/age/30.html)
うーん...