hirax.net::Keywords::「コンピュータ」のブログ

■「技術」が作る「人の姿」　

　from 「n年前へ」

グーテンベルグ(印刷技術)は全ての人を読者に変えた。
ゼロックス(コピー機)は全ての人を出版者に変えた。
コンピュータは全ての人を書き手に変え、
インターネットは人をコメンテータにしてしまった。
コメント欄溢れる各種ツールを使っていると、
「コメントをつけるだけの人」になってしまいそうだ。

■「勝ち」≒「価値」という方程式　

　「将棋電王戦」の憂鬱を読んで思い出した、８年前にサンノゼで書いた記事（「プロ棋士と将棋ソフトの対局許可」と「競技（スポーツ）の本質」）。

　こういったゲームの世界で、(人間が作り出したはずの)コンピュータに人間が太刀打ちできないということが増えていくのかもしれません。
　しかし、「相手に勝てないから（そんな勝負が）つまらない」かというと、それは違うように思います。今年、コンピュータと戦ったチェスチャンピオンのカジムダノフが「人間とコンピュータの対決」に関して、かつてこう語っています。
　”Sports are not about reaching a result. Sport is about developing your inner qualities.”（競技（スポーツ）は記録や勝ちを手に入れるためのものではない。それは、私たちが自分の中にある価値を成長させるためのものだ。）

　もちろん、…その勝負に負け続けるだけであれば、それはつまらく面白くない気持ちにもなるの確かでしょう。けれど、（強いコンピュータに鍛えられて）自分の将棋の腕が強くなることも、またひとつの事実であるかもしれません。

　「たいていのスポーツは、勝った試合より負けた試合から多くを学ぶもんだろ」

■最高に楽しい！”６０年代から８０年代のコンピュータが動いてる ”Living Computer Museum　

　Living Computer Museum はコンピュータにハマったことがある中・老年には麻薬のような存在です。それは、コンピュータにハマったことがない、もしくは、中・老年でない人たちには、退屈極まりない場所かもしれません。…けれど、ある種の人たちが此処に行けば、必ずハマ（キマ）ること間違いありません。

　マイクロソフト社の（ビル・ゲイツとの）共同創業者ポール・アレンが設立したLiving Computer Museumには、６０年代から８０年代の時代を作ったメインフレーム・マイクロコンピュータ・マイコンピュータ・パーソナルコンピュータたちが、いじり・触れる状態で（ちゃんと）動いています。

　たとえば、下のインタラクティブなパノラマ写真（その他のパノラマ写真はこちらから）は、その一角（マイコンの時代）で撮影したものです。XeroxのAltoを動かすことができたり、Apple][やAtraiやTRS-80やPETやVIC-20(日本名 VIC-1001)･･･そこには、あの時代が詰まってます。

　Living Computer Museumは、シアトル・ライト・レールのSODO駅近く（徒歩10分くらい）にあります。一人で行けば（かなりの高確率でマンツーマンになりそうな）４５分ほどのガイドツアーを楽しむこともできます。ある種の人たちには、コンピュータにハマったことがある中・老年には…とてもお勧めな「場所」だと思います。

　The Living Computer Museum also fulfills my hope that the achievements of early computer engineers aren't lost to time. I wanted to provide a website and repository that recognized the efforts of those creative engineers who made some of the early breakthroughs in interactive computing that changed the world.

Letter from Paul G. Allen

■100円程度の小さな工夫，スマホセンサをこんな活用するなんて！　

　4月18日発売の「ソフトウェアデザイン（Software Design） 2019年5月号」に 『100円程度の小さな工夫，スマホセンサをこんな活用するなんて！』を書きました。スマホが持つセンサや入出力端子を、少し使い方を変えたりすることで、AR可視化機能を拡張してみよう！という話です。

　東京の山近く、東青梅に位置する「夢の図書館」「マイコン博物館」で「コンピュータの歴史を学ぶセミナー」に参加した後、そこで（コンピュータの歴史に詳しい人に）相談した後に秋月電子に行って部品を買い、NeXTコンピュータの開発をしていた人などに（JUNETとfjの話題を振り返りつつ）回路の相談をしつつ、そんなこんなが反映されているような（反映されていないような）そんな感じのスマホ電子工作記事になります。

■「エクセルの計算順序」から「コンピュータの歴史」を感じよう！　

-2020年になった今、1950-1980の時代を振り返る-

-1^2の計算結果は-1になる！？「エクセルの計算順序」の謎

　オフィス作業の多くがMicrosoft Excel（エクセル）上で行うのが当たり前となっています。そのエクセルでシートを開き、”= 0 - 1^2”, “= -1^2 + 0”という2式をセルに入力すると、どんな計算結果が出力されるでしょうか？

「どちらも-1になるはず」と答える人が多いかもしれませんが、実際に式をセルに入力すると、”=0 - 1^2→ -1”, “=-1^2+0→1”という結果になります（図１(a)）。だからといって、「エクセルの計算バグ！？」と考えてはいけません。なぜなら、これは伝統正しいエクセルの仕様だからです。

同じ“-”でも二項演算子の”-”と単項演算子の”-”がある？

「どちらも-1になるはず」という答は、２式をそれぞれ0 –(1^2)と-(1^2)+0という順番に暗算から得られたはずです。…けれど、エクセルが行う計算順は、それとは違う0 –( 1^2)と(-1)^2+0という順番です。その結果、 -1と1という計算結果をエクセルは得るのです。

「減算よりべき乗の演算の方が優先されるべきだから、エクセルの計算順はやはりおかしくない？」と思う人もいるかもしれません。しかし、エクセルも、2つの値間でべき乗計算を行う”^”は、減算を行う“-”より優先する仕様になっています。

　この2式には、”-” ”^” ”+”という演算子が登場します。そのうちの、”^”と”+”についてはすべて、左右の2値を使い演算を行う2項演算子です。ところが、”-”については、”= 0 - 1^2”では（被演算子が左右にある）2項演算子ですが、“= -1^2 + 0”については、（被演算子が左右の片方にしかない）演算で使う値が一個の単項演算子(Unary operator)として、エクセルの計算が行われます（図１(b)）。

“= -1^2 + 0”の”-”は、”-”の右側にある1を符号反転させる演算子で、エクセルが採用する演算子優先順では、単項演算子は二項演算子に優先します（図１(c)）。その結果として、-1^2+0は (-1)^2+0 として計算されて、1という値が出力されるのです。

コンピュータを広めた表計算ソフトが生まれた時代の計算順を調査しよう！

エクセルの演算順序が、一般的な代数式の計算順序と異なる仕様になった理由はわかりません。「エクセルが開発された当時、標準的に使われていたLotus 1-2-3との互換性を考えたのではないか？」とも思いたくなりますが、そうでもありません。

　なぜなら、Lotus 1-2-3では、エクセルと異なる-1^2=1という計算結果になるからです。また、1985年発売のエクセルの開発チームは、Lotus 1-2-3(1983年発売) に先行して1982年発売のMultiPlanも開発しましたが、Multiplanでもやはり-1^2=-1と計算していたからです。

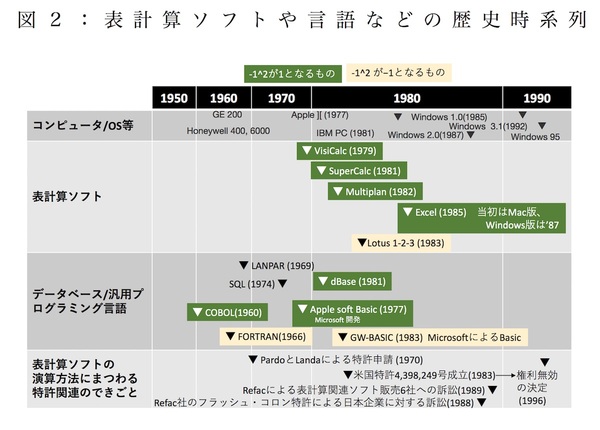
　エクセルやMultiplanが発売当時を調べてみると、面白いことがわかります。表計算ソフトという形態を作り出したVisiCalcも、当時の表計算ソフトの用途と重なるところも多かったデータベースソフトdBaseでも、ビジネスプログラミング言語のCOBOLも、多くのソフトでエクセルと同じ演算結果を出力します（図2、図3）。 　そんな時代背景を踏まえれば、エクセルが「単項演算子―は2項演算子^に優先する」という仕様にしたということも、いたって自然にも思えてきます。

セル間の計算順序には「2つの方法」が使われている

　「セル間の演算を簡単にできる」のが、今ではエクセルに代表される表計算ソフトウェアです。だから、エクセル等が計算を行う際には、セル内の演算順だけでなく、セル間の計算順序もきちんと決まっていて、エクセルでは、2つの異なるセル間の計算方法が使われています。

「依存関係ごとに、値が定まるものから先に」の計算順

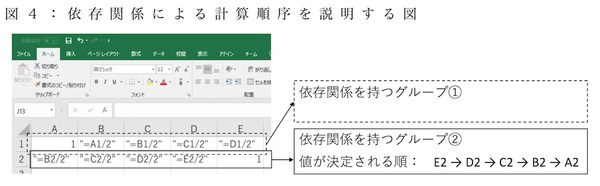
通常使われているセル間の計算順は、「セル間の依存関係を（ツリー構造で）辿り、値が定まっている“源流“から計算を順に行っていく」というものです。たとえば、セルB2に”=10-B3”、そしてセルB3に”6”という文字が入力されていたら、まずは「セルB2の前に、セルB3を定義する」という依存関係を持つグループの中で順番を生成した上で、セルB3を表す変数に値6を設定し、そしてB3で10-6という演算を行って、結果の4を格納するのです。もしも、ユーザーがどこかのセルを書き換えた時には、そのセルが属する依存関係のグループ内のみで、上流から下流に向かって計算が行われます。

アルファベット順＋Zの法則（左→右、上→下）の計算順

もうひとつのセル間計算順は、「通常の方法が使えない場合」に使われます。具体的には、自己参照（循環参照）が行われている場合、言い換えれば「依存関係を辿っていくと、いつの間にか自分に辿り着いてしまい、無限ループに陥る場合」に使われます。計算をするのに、自分（自セル）自身の値を入力（右辺値）として使う状況があるの？と感じられるかもしれません。けれど、方程式を解く必要がある場合など、自己を参照するような数式に対する計算ができると便利なことも多いのです。

　たとえば、x ==(2 -3 y) / 4, y == (5 – 6 x) / 7という一次連立方程式を解きたい場合、セルB1とB2をxと yだとした上で、それぞれに =(2 -3*B2)/4と =(5 - 6*B1)/7という式を入れてみます。すると、「循環参照が行われています・・・」という警告が出るので、設定を「反復計算を使う（計算回数はとりあえず100）」と変えて、反復計算を実行させる（F9を押す）と、x(B1)=-0.1, y(B2)=0.8と連立方程式の計算結果が求まります。

　反復計算を行う場合には、循環参照が行われている部分に対し、アルファベット順で前方のシートから、そして同じシート内では左から右へ・上から下への順で（A1からA行を左から右へ、次はB行を左から右へ…と）計算が行われます。そして、最大反復回数に達するか、各セルでの計算結果の変化値が所定の値を下回るまで、この計算が繰り返されるのです。

　循環参照による反復計算は、普通とは言えないかもしれません。とはいえ、方程式を解いたりする場合などには必須になることも多い計算手法です（＊この方法では、必ずしも計算が収束するわけではありません）。

表計算ソフトが生まれた頃は、反復計算方式が使われていた

表計算ソフトが登場したての’80前半、すべての表計算ソフトが、どのような計算であっても、反復計算方式を使っていました。もう少し正確に言えば、シートに含まれるセルに対して（Zの法則など）所定の順番で計算を行い、値が変わらなくなるまでユーザが手動で計算を繰り返していました。

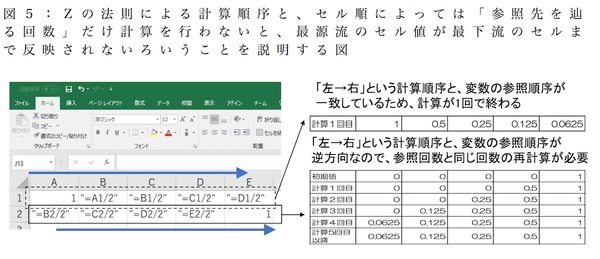
　「値が変わらなくなるまで再計算を行う」必要がなぜあるかというと、他のセルを参照する計算式が使われている場合、セルの並び順によっては「参照先を辿る回数」の再計算を行わなければ、最源流のセル値が最下流のセルまで反映されないからです（図4）。そのため、初期の表計算ソフトを使う際には、セルの値を見ながらユーザが計算を繰り返さなければならなかったのです（図5）。

　最源流のセルから下流へと「依存関係に沿って計算していく方式」が一般的に用いられるようになってから、各セルに対し1回の計算だけで結果が得られるという、現在の表計算ソフトの形態に落ち着いたのです。

表計算の計算方法を提案する「幻の基本特許」が存在していたが…

「依存関係を踏まえ、上流セルから計算を行う」という表計算ソフトの土台ともなっている演算手法ですが、実は「幻の基本特許」があります。

今の表計算ソフトの原型となったVisiCalcが登場する1979年より10年も前の1969年、LANPARというデータ操作言語が米国人Rene PardoとRemy Landaにより開発されます。LANPARが採用した変数間の演算順序は、automatic forward referencing (natural order calculation)と呼ばれ、「値が定義されているものから先に計算を行う」という表計算の計算順序に関する基本アルゴリズムと言えるものでした。

申請から13年を経て成立した特許で、さらに6年後に訴訟開始

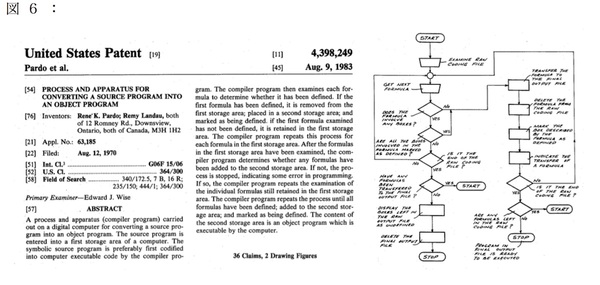
PardoとLandaは、1970年に計算手法に関する特許申請を行いましたが、「技術の内容説明が不足」という理由で申請は却下されます。しかし、彼らは特許成立に向けた活動を続け、「プログラミングに関わる一般知識を持つ通常の人であれば、特許で公開された内容から技術を再現できる」とする一般の3名のプログラミング経験者による宣誓書を提出することで、特許申請から13年を経た1983年、米国特許4,398,249号としてようやく認めさせます（図6）。

そして、すでに表計算ソフトが必需品となっていた1989年、Pardoらは、「1ヶ月以内に少なくとも2名の特許侵害者を訴える」という条件付きで、パテント・トロール企業として有名なRefacに特許権利の5％を譲渡します。Refacは、デジタル時計の表示に関する特許、「時と分表示の間にあるコロンを点滅させる」というフラッシュ・コロン特許で、日本企業を中心に100億円以上の特許使用料を得た企業です。

そんな経緯を受けて、Refacは表計算ソフトを販売していた6社、Lotus(Lotus 1-2-3), Microsoft(Excel), Borland(Quattro), Ashton-Tate(Full Impact), Computer Associates(SuperCalc), Informix(Wingz)に対して、膨大な特許使用料を請求する訴訟を起こします。権利期間17年にわたる特許使用料として、膨大な金額を請求する訴訟です。

「特許内容は十分」と宣誓したプログラミング経験者、実は…

「表計算ソフトの基本特許は、膨大な特許使用料を生み出した」という結末を迎えたかというと…そうではありませんでした。その訴訟の結果は「大どんでん返し」で終わります。

1989年に始まる審判で、「Pardoらの特許申請には不正があり、権利無効である」とLotusが主張したのです。どういうことかというと、「特許内容は十分詳細である」と証言したプログラミング経験者というのが、実はLANPERの開発経験を持つ関係者で、その事実を特許商標局に対して隠していたというのです。「特許申請に対して全く前提知識を持たない人であっても、技術内容を理解できる」という意見を述べる宣誓であるはずが、実はそうではないものを提出していたことを「不正」と判断されたのです。そして、1996年、表計算ソフトの演算手法に関する基本特許とも言える米国特許4,398,249号は、「権利を行使できない幻の特許」と決定されたのでした。

表計算ソフトの演算順…そこには「面白い歴史」が詰まってた

個人でコンピュータを使えるようになった20世紀の後半も、あるいはＰＣがあたりまえの道具になった21世紀の今現在も、その価値や原動力となっているのが表計算ソフトです。そんな表計算ソフトの演算（計算）順を今回は調査してみました。意外なほど、たくさんのエッセンス、とても興味深いコンピュータの歴史がそこには詰まっていました。