hirax.net::Keywords::「複素平面」のブログ

■「"複雑極まりない"複素平面」上に「仕事」と「趣味」を描く　

　複素平面"complex plane"は、複素数"complex number"の実部をx軸(実軸=real axis)・虚部をy軸(虚軸 = imaginary axis)にプロットしたものである。3+2iという複素数であればxy平面にx=3,y=2にを示す、そんな平面が複素平面だ（iは虚数単位=2乗した時に-1になる数である）。

　『「仕事」と「趣味」を2次元マップで1分以内に描け』言われたら、あなたならどう描くだろう？(同世代の)"Schemeを愛するプログラマ"が描いた「趣味と仕事の関係を描いた2次元チャート」を眺め、ふと私も「仕事」と「趣味」のイメージを2次元マップに描いてみたくなった。

　趣味を訊かれるといつもちょっと困る。私には趣味と仕事の違いがよくわからないからだ。
　　　Shiro Kawai

　人によって「仕事」と「趣味」というものの捉え方は違うだろうけれども、できる限り一般的に「仕事」と「趣味」という領域を2つの軸上に配置させるとしたら、どのように「仕事」と「趣味」を描くだろう？そんなことを「クイズの回答者になった気分で」描いてみたら、それは「複素平面」だった。(その人自身に対する)実利的・物質的でまさにリアルな"Real axis"と、イメージ的な「心の軸」を示す"Imaginary axis"というまさに実軸・虚軸で表現された複素平面である。

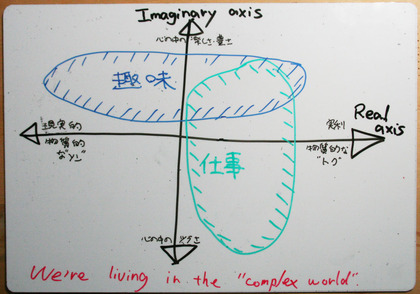
　この複素平面の縦軸(の上方向)は、自分の心を豊かにする軸と捉えることができるだろう。「虚」という文字よりは、"Imaginary"という文字で捉えたい「(その人自身の)心の満足」を示す軸、である。
　そして、横軸（の右方向）は、その人自身を実利的に満足させる軸である。しかし、その自分への「実利」という軸は、実は他人が何らかの形で価値を感じたことを示す軸でもあると思う。なぜなら、その「実利」は「他者が得た価値」が回りまわって流れてきたものに違いないからである。他人が得た満足が姿を変えたものであるから、である。つまり、この複素平面の横軸は「自分への実利」を示す軸であると同時に「他者を豊かにする軸」なのである。

　ひとことでまとめてしまえば、この複素平面は「本人(自分)の満足」と「他人の満足」という２つの軸で形作られる平面なのだ。

'Cause we are living in a material world. You know that we are living in a material world.
　　Madonna "Material Girl"

　その人ごとに「仕事」と「趣味」の位置づけがあると思う。どんな軸を使って、どんな風に「仕事」と「趣味」を捉えるかは、みなそれぞれ違うはずだ、と思う。「自分の中で辛さを感じながら、実利を得る仕事」もあれば（右下の象限）、「自分自身の楽しさとともに実利を得る仕事」もあるはずだ（右上の象限）。そして、さらに言うならば、同じ仕事であったとしても、その仕事がどこに位置するかは、人それぞれ異なっているだろう、と思う。そして、同じ一人の人がする同じ仕事であったとしても、きっと「その捉え方」「その座標」は変化し・移動していくものだろう、と信じている。

俳諧で「虚実」ということがしばしば論ぜられる。数学で、実数と虚数とをXとYとの軸にとって二次元の量の世界を組み立てる。虚数だけでも、実数だけでも、現わされるものはただ「線」の世界である。二つを結ぶ事によって、始めて無限な「面」の世界が広がる。
　　　寺田寅彦　「無題六十四」

　もしも、上に描いた複素平面="Complex plane"、それを言い換えれば言葉通りの「複雑極まりない世界」の上に、今のあなたが抱えているだろう「仕事」と、あなたが楽しんでいるかもしれない「趣味」は、どんなXY座標上にプロットされるだろうか。"複雑極まりない"複素平面上に、あなたはどんな軌跡を描いているだろうか。

■百次方程式の係数を複素平面上で動かして、百個の解のダンスを眺め・楽しんでみよう!?　

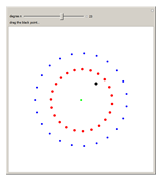　多項式からなる代数方程式の「係数」をマウスでつかんで動かした時に、「（その代数方程式の）”解たち”の配置」と「”解たち”が動き回るようす」を眺めたいな…と思ったのですが、ググってみると「x^n + b x + 1 = 0 おいう代数方程式の係数bを複素平面上で動かした時に”解たち”がどのような配置になるか・どのように動き回るか」をインタラクティブに味わえる・楽しむことができる（Monodromy of z^n + b z + 1 = 0）というものがありました。

　そこで、”x^n + b x + 1 = 0”という二次から百次までの代数方程式で、係数”ｂ”を複素平面上で（マウスで）動かして（青丸）、（その動きに応じて）解の集団（赤丸）が形作る美しいダンスを眺め・楽しんでみました。

　中学生くらいの頃、"X^2+2=0"といった方程式を（各々の軸が実数の）XY平面上で黒板の上で眺めつつ、その黒板上に描かれたXY平面には、"Y＝X^2+2"というグラフと"Y=0"というグラフが「どこでも交わっていない」ようにしか見えないのに、方程式の「答え」は「（どこかに）２つの解がある」というもので…それは理不尽で不思議で…つまりは納得できなかったような気がします。

　あの頃、複素平面上に複素数値を描いたグラフを見ていたら、黒板の上で多項式の解が複素平面上で円を描いてフォーク・ダンスを踊る風景を眺めていたら…数学に恋をしていたかもしれない、と思います。

　オクラホマ・ミクサーやマイムマイム…黒板の上の複素平面上で代数方程式の係数が動くにつれ、その方程式の解の群団が踊るフォークダンス…が今日見た景色、です。