2012-04-17[n年前へ]
■百次方程式の係数を複素平面上で動かして、百個の解のダンスを眺め・楽しんでみよう!? 
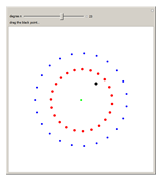多項式からなる代数方程式の「係数」をマウスでつかんで動かした時に、「（その代数方程式の）”解たち”の配置」と「”解たち”が動き回るようす」を眺めたいな…と思ったのですが、ググってみると「x^n + b x + 1 = 0 おいう代数方程式の係数bを複素平面上で動かした時に”解たち”がどのような配置になるか・どのように動き回るか」をインタラクティブに味わえる・楽しむことができる（Monodromy of z^n + b z + 1 = 0）というものがありました。
そこで、”x^n + b x + 1 = 0”という二次から百次までの代数方程式で、係数”ｂ”を複素平面上で（マウスで）動かして（青丸）、（その動きに応じて）解の集団（赤丸）が形作る美しいダンスを眺め・楽しんでみました。
中学生くらいの頃、"X^2+2=0"といった方程式を（各々の軸が実数の）XY平面上で黒板の上で眺めつつ、その黒板上に描かれたXY平面には、"Y＝X^2+2"というグラフと"Y=0"というグラフが「どこでも交わっていない」ようにしか見えないのに、方程式の「答え」は「（どこかに）２つの解がある」というもので…それは理不尽で不思議で…つまりは納得できなかったような気がします。
あの頃、複素平面上に複素数値を描いたグラフを見ていたら、黒板の上で多項式の解が複素平面上で円を描いてフォーク・ダンスを踊る風景を眺めていたら…数学に恋をしていたかもしれない、と思います。
オクラホマ・ミクサーやマイムマイム…黒板の上の複素平面上で代数方程式の係数が動くにつれ、その方程式の解の群団が踊るフォークダンス…が今日見た景色、です。
」など。