2013-11-01[n年前へ]
■11月2・3日はMaker Faire Tokyo 2013で会いましょう! 
 今週末、11月3日(Sun)と4日(Mon)、東京お台場の科学未来館で開催されるMaker Faire Tokyo 2013に「Twitter連動バブルジェットディスプレイ」を出展します(科学未来館一階,オリエンテーションルーム N-12ブース)。
今週末、11月3日(Sun)と4日(Mon)、東京お台場の科学未来館で開催されるMaker Faire Tokyo 2013に「Twitter連動バブルジェットディスプレイ」を出展します(科学未来館一階,オリエンテーションルーム N-12ブース)。
Maker Faire は面白い奇妙な工学技術自作グッズがたくさん並ぶ祭典ですから、モノを作る・作ったものを見るのが好きな人は遊びに行くと面白いかもしれません。開催時間は、3日(日)は12:00~17:00、4日(月)は10:00~17:00です。

3日・4日の両日とも、開催時間中は、ブース辺りで所在なくぼおっと立ってると思いますので、お気軽に声をお掛け下さい。また、ブース辺りに姿が見えなく・近くをウロウロ右往左往しているようでしたら、@hirax, jun@hirax.netにでも、適当に声をお掛け下さい。
それでは、11月2・3日はMaker Faire Tokyo 2013でお会いしましょう!
2013-11-04[n年前へ]
■続 Maker Faire Tokyo 2013 に行ってみる!? 
 Maker Faire Tokyo 2013 、「ラスト三十分」と「泡に呟かせ・バックステージから記念撮影をして・展示を半ば終了させて…他の展示を眺めに行きました。この時間になると眺めている人の数が減ってきて、ゆるりと楽しむことができて・とても心地良い感じです。
Maker Faire Tokyo 2013 、「ラスト三十分」と「泡に呟かせ・バックステージから記念撮影をして・展示を半ば終了させて…他の展示を眺めに行きました。この時間になると眺めている人の数が減ってきて、ゆるりと楽しむことができて・とても心地良い感じです。
「STAR TREKのソースプログラムを印字したもの」とか「無限音階シンセ」とか「超静音トイレットペーパー」とか「空を心地良く飛び続けるたくさんの飛行機」とか…そんなものを眺めていると、つまり発想力やそんなものを作ってみようと思う行動力・技術力を眺めていると、何だかとても面白くて、あっという間の気持ち良いけれど・とても短かな自由時間でした。
やまねこ@楢ノ木技研 @felis_silv さんのところで見かけた「巨大水晶発振器」 14kHzの高音が哀しいくらい(私の耳には)聞こえなかった。で、iPhoneで音を確認すると、綺麗に音が出ている…。うぅ。
2013-11-05[n年前へ]
■水が金網の上で・指に押されて転がる日 
 一週間前の夜、六本木の古民家で、いくつかの「新技術」を体験してきました。そんな新技術の中のひとつが、超撥水性の塗料材料です。疎水基が先端にあるトゲトゲ・イガイガ形状のシリカでコーティングすることで、表面付着力を通常の百分の一近く下げた…という材料です。
一週間前の夜、六本木の古民家で、いくつかの「新技術」を体験してきました。そんな新技術の中のひとつが、超撥水性の塗料材料です。疎水基が先端にあるトゲトゲ・イガイガ形状のシリカでコーティングすることで、表面付着力を通常の百分の一近く下げた…という材料です。
「コップに水を入れて目の細かい金網で蓋をすると、コップを逆さにしても(表面張力のために)水がこぼれない」なんてビックリ実験ネタがありますが、この超撥水性塗料を金網に塗ると、その上に水を優しく載せると、水はスライムのように気持ち良く転がり動くだけで、金網をすり抜け・滴り落ちることもありません。
周りから力が掛からないければ、水は「丸くちぢまっている」のが自然というわけで、(地球の重力はなくせないにしても)表面付着力を限りなく小さくすると、水は滑らかで何やら丸っこい塊に変身します。その水の塊が見せる不思議な風景と、その水に触れると味わうことができる心地良い感覚は、何だかとても気持ちが良くて…そんな快感をお伝えしたくて、こんな動画を撮影してみました。
2013-11-06[n年前へ]
■非現実的な「ネズミ入りフォースフィードバックマウス」と超現実的な「睡眠・夢状態の可視化」 
先週末、Maker Faire Tokyo 2013 (MTF2013)に朝から晩まで浸かっていた影響か何なのか…こんな夢を見ました。夢を見たのは、初日11/3(日)の夜から11/4(月)の朝にかけて、です。
 私は、どうやら、フォースフィードバックマウスを作ろうとしているようで、大きな「コンピュータ操作用のマウス」の中にネズミを入れて、そのネズミの周りにぶら下げるエサの方向を動かすことで・ネズミの動きを変化させて、手にしたコンピュータマウスが引っ張られる感じ(フォースフィードバック)を受けるという仕組みを作り出そうと四苦八苦しています。…結構苦労しているらしきことが、ネズミが周りのものを囓(かじ)りまくるのでコンピュータマウスを掴む指を、腹減ったネズミが時折噛んでしまう、という問題のようです。…ワケのわからない夢です。
私は、どうやら、フォースフィードバックマウスを作ろうとしているようで、大きな「コンピュータ操作用のマウス」の中にネズミを入れて、そのネズミの周りにぶら下げるエサの方向を動かすことで・ネズミの動きを変化させて、手にしたコンピュータマウスが引っ張られる感じ(フォースフィードバック)を受けるという仕組みを作り出そうと四苦八苦しています。…結構苦労しているらしきことが、ネズミが周りのものを囓(かじ)りまくるのでコンピュータマウスを掴む指を、腹減ったネズミが時折噛んでしまう、という問題のようです。…ワケのわからない夢です。
 その夢を、私がどんなシチュエーションで見ていたのかとても知りたかったので、自分の睡眠状態の推移を眺めてみた結果が、下に貼り付けたグラフです。
その夢を、私がどんなシチュエーションで見ていたのかとても知りたかったので、自分の睡眠状態の推移を眺めてみた結果が、下に貼り付けたグラフです。
私の記憶では「ネズミ入りフォースフィードバックマウス」の夢を見たのは、起床する寸前というわけではありませんでした。…ということは、朝の1時か3時のREM睡眠の終わり近くか、朝4時頃の深睡眠から覚醒する直前に、「ネズミ入りフォースフィードバックマウス」研究をしていたようです。
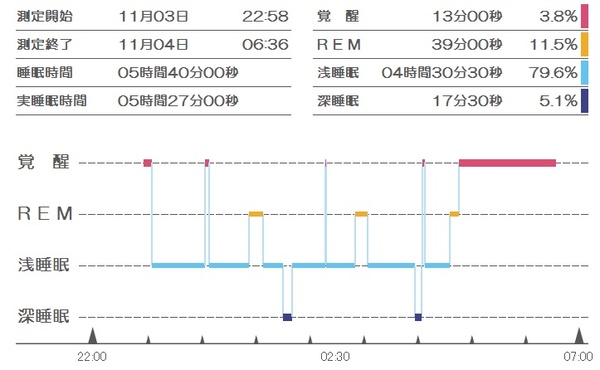
というわけで、MTF初日が終わった夜、新橋駅前ビルで飲んで…23時には眠りについて、Maker Faire Tokyo 2013の興奮の余韻を引きづりつつ浅い眠りを続けた後に、日付が変わってから、夢の中で(非現実的な)ネズミ入りフォースフィードバックマウスの開発をしていた「睡眠・夢状態」を可視化してみた…のが今日見た科学的グラフです。
2013-11-07[n年前へ]
■「近代麻雀オリジナル」連載 最終回! 
 近代麻雀オリジナルで書いてた連載が、明日発売の12月号で最終回です。今年の春頃は、(やっぱり連載をした)アスキーPCが休刊し、今度は近代麻雀オリジナルが少し似たようなシチュエーションです。
近代麻雀オリジナルで書いてた連載が、明日発売の12月号で最終回です。今年の春頃は、(やっぱり連載をした)アスキーPCが休刊し、今度は近代麻雀オリジナルが少し似たようなシチュエーションです。
すると、集めた数百個の文章中で、条件に当てはまる言葉はたったひとつ、"Here's looking at you, kid."でした(Here's = 乾杯)。
アスキーPC 「ぐるぐるサイエンス~最後の暗号」
月毎(ごと)に何かを考え・形にしなければならないというルーチンワークが課せられていると、それをキッカケにして新しい気づきや発見をすることが多いので、そういう機会が無くなってしまうと、何だか少し残念です。
だから、そんな後悔をしないために…というわけではないですが、色んなことをやってみよう・誘われたら(基本的に)イエス!と言おう、とつくづく思う今日この頃です。
…so let's give'em hell
wish everybody well
here's to us
here's to love
Halestorm "Here's To Us"
 そういえば、今年は「週刊 大衆」の連載オファーがありました。…もしも、その話をお受けしていたら、一体どんな毎月の「新しい気づき・発見」があったのだろう?と考えます。そして同時に、もしもその話を受けていたら、今頃「週刊 大衆」も休刊していたのだろうか…とガタガタブルしてみたりもするのです。
そういえば、今年は「週刊 大衆」の連載オファーがありました。…もしも、その話をお受けしていたら、一体どんな毎月の「新しい気づき・発見」があったのだろう?と考えます。そして同時に、もしもその話を受けていたら、今頃「週刊 大衆」も休刊していたのだろうか…とガタガタブルしてみたりもするのです。
2013-11-10[n年前へ]
■バンコクの「昔の秋葉原!?風な場所マップ」 
 今を原点にすると懐古的・ノスタルジックに思えるかもしれない「電気」系匂いがプンプンする場所(けれど、何だかエネルギーを与えてくれるように思える)が好きな人のために、バンコクの「昔の秋葉原!?風な場所マップ」を作ってみました。描いてみたのは、バンモー周辺(参考1・参考2)・クローントム周辺(参考3)、サパーレック周辺(参考4)です。どの地区も、場所を知らないと見つけづらかったり・見つけても場所を忘れてしまったり、そこに行っても中の広がりに気づかなかったりします。…そこで、せめて何度でも行けるようにと、地図を作ってみたわけです。
今を原点にすると懐古的・ノスタルジックに思えるかもしれない「電気」系匂いがプンプンする場所(けれど、何だかエネルギーを与えてくれるように思える)が好きな人のために、バンコクの「昔の秋葉原!?風な場所マップ」を作ってみました。描いてみたのは、バンモー周辺(参考1・参考2)・クローントム周辺(参考3)、サパーレック周辺(参考4)です。どの地区も、場所を知らないと見つけづらかったり・見つけても場所を忘れてしまったり、そこに行っても中の広がりに気づかなかったりします。…そこで、せめて何度でも行けるようにと、地図を作ってみたわけです。
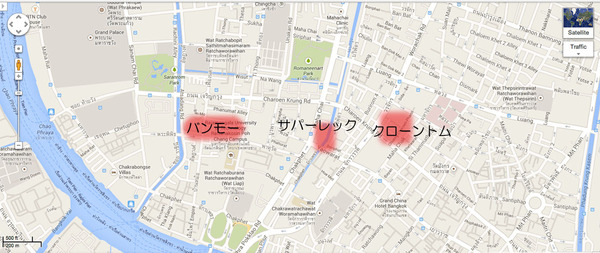
これらの電脳ダンジョンのワナは、「場所を知らないと行きづらい」ということだけではありません。たとえば、バンモーの中心にあるバンモープラザの2F(東京ラジオでバートみたいな感じ)になかなか気づいて・2Fまで行くことができない…とか、クローントムはクローントムセンターの周りだけでなく、通りを越えた辺り全体に面白いものを取り扱ってる店・屋台が続いているので…途中で(全部眺めることを)間違いなく挫折してしまう…といったことがあります。
けれど、そんな行きづらい・気付きづらい場所だなんてことは、知っていれば(さほど)ワナにはならない…ということで、今日はこんな地図を作ってみました。
朝7時、クローントム(旧 泥棒市場)に自転車で行く。自転車を置いて建物の中をじっくり長く眺めたいけれど、自転車をどこかに持ってかれしまうのも困る…。
どこの誰にも開けられそうにないチェーンロックも屋台で安く売ってるけど、その屋台の隣では、どんなチェーンも切断できそうなチェーンカッターが売られてる。まさに天下の「ほこ×たて」状態。
朝7時、クロントム(旧 泥棒市場)に自転車で行く
2013-11-11[n年前へ]
■サッカー場に匹敵する超巨大な偵察衛星!?赤道上空3万6千kmから自宅ルータに侵入可能!? 
サッカー場に匹敵する超巨大な偵察衛星!?赤道上空3万6千kmから自宅ルータに侵入可能!?を書きました。
約7年前、アルミホイルで作った自作パラボラアンテナを使い、他者のインターネット通信機器(ルーター)から出る微弱電波を増幅してインターネット接続を行った(らしい)というインターネット・オークション・サイトへの不正接続事件がありました。 その事件で使われた「アルミホイル製の自作パラボラアンテナ」の大きさが直径30センチメートルなので、ORION衛星のパラボラアンテナ直径100メートルというのは直径にして333倍、面積にして11万倍にも達します!
2013-11-13[n年前へ]
■「エロ雑誌」や「少女マンガ雑誌」の発行部数 
「エロ本業界の厳しすぎる現状」を読み、エロ雑誌の発行部数が知りたくなりました。そこで調べてみると、おおよそ20万部前後のようです。20万部と言われても、それが多いのか少ないのかよくわかりません。…そこで、休刊&抜本的リニューアルをするという近代麻雀オリジナルの発行部数を眺めてみると16万部…それと大差がない部数だということは、エロ雑誌もなるほど苦しいのかもしれないと納得します。
 その一方で、たとえば、少女マンガ雑誌の公表印刷部数を眺めてみると、これまた20万部を下回る程度のものばかり…。発行部数の時系列推移を眺めてみると、実に見事なくらいに右肩下がりです。
その一方で、たとえば、少女マンガ雑誌の公表印刷部数を眺めてみると、これまた20万部を下回る程度のものばかり…。発行部数の時系列推移を眺めてみると、実に見事なくらいに右肩下がりです。
たとえば、週刊SPA!のように「若い人向け雑誌」だったはずが「いつのまにか中年向け雑誌」になっていたりするものを多く見かけます。しかし、たとえば、こんな言葉を読むと「そうせざるをえないんだな」と感じさせられます。
「今までの出版界は、雑誌は読者層の中の若いほうにあわせて作ることがセオリーと言われてましたが、今それをやっていたらどんどん売れなくなると思います」「若い子は読まなくていい」「今の読者を卒業させない」
出版不況と『百合姫』リニューアル中にある引用から
 そういう「縮小スパイラル」に陥らないのは、年代別の雑誌をとりそろえて、読者を徐々に別の雑誌に誘導していくようなファッション誌くらいなのだろうか?と考えたりします。
そういう「縮小スパイラル」に陥らないのは、年代別の雑誌をとりそろえて、読者を徐々に別の雑誌に誘導していくようなファッション誌くらいなのだろうか?と考えたりします。
2013-11-14[n年前へ]
■「どんな便秘も退治する強力な下剤」と「お腹のユルユルを絶対抑える下痢止め」のホコ×タテ勝負!? 
ニンニクの厚切りスライスが「これでもか!」と入った豚肉炒めが美味しく、心ゆくまで食べました。…食べて数時間後、ひっきりなしにトイレの神さまならぬ、腹を下した人になってしまいました(何しろ、昨夜は3時間くらいトイレに籠もったくらいです)。
 …そこで、薬局に行き「下痢止め下さい~」と若い青年店員に伝え、「はい、これです!」と渡された丸薬を何錠も飲みました。…宿に戻ってから、その丸薬 "Dulcolax"の服用法を確認してみると、まず「便秘解消のための薬=下剤です」と書いてあります。…こ・これは、とてもまずい事態です。下痢を止めたいのに下剤を飲んでしまうとは…。
…そこで、薬局に行き「下痢止め下さい~」と若い青年店員に伝え、「はい、これです!」と渡された丸薬を何錠も飲みました。…宿に戻ってから、その丸薬 "Dulcolax"の服用法を確認してみると、まず「便秘解消のための薬=下剤です」と書いてあります。…こ・これは、とてもまずい事態です。下痢を止めたいのに下剤を飲んでしまうとは…。
 しょうがないので、脂汗を流しつつ、もう一度同じ薬局に行って、今度こそ「下痢止め」を買い(青年店員は非常に微妙な表情をしている…)・もちろんすぐにガブ飲みします*。何しろ、下痢状態なのに下剤を飲んでしまっているわけですから、その下剤の勢いを何としても止めなければなりません。
しょうがないので、脂汗を流しつつ、もう一度同じ薬局に行って、今度こそ「下痢止め」を買い(青年店員は非常に微妙な表情をしている…)・もちろんすぐにガブ飲みします*。何しろ、下痢状態なのに下剤を飲んでしまっているわけですから、その下剤の勢いを何としても止めなければなりません。
…一体、「どんな便秘も退治する強力な下剤」と「お腹のユルユルを絶対抑える下痢止め」…この(切実だけれど、くだらない)ホコ×タテ勝負は、一体どちらに軍配があがるのでしょうか…? **
-------------------
* よくよく考えると、薬局で薬を買って・すぐにガブ飲みする行為が「負のスパイラル」を生んでいるようです。
** 下剤(+もともとの下痢パワー)が勝ち、下痢止めは打破されてしまいました…。
2013-11-15[n年前へ]
■BS朝日「ジュリアス・シーザーの叫び」のお手伝い 
 BS朝日で11月17日に放送される「ジュリアス・シーザーの叫び」で「エンジニアリングの結果生み出された面白いもの」を眺めてみようという内容が扱われます。その狂言回し的なお手伝いをしてきました。
BS朝日で11月17日に放送される「ジュリアス・シーザーの叫び」で「エンジニアリングの結果生み出された面白いもの」を眺めてみようという内容が扱われます。その狂言回し的なお手伝いをしてきました。
 「エンジニアリングの結果生み出された面白いもの」は(自分が眺めてみたいばかりに、急遽 @GOROman さんにデモをお願いした) Oculus Rift や、○×な△□といったグッズです。そんな何かに興味がある人は、少し眺めてみると面白いと思います。
「エンジニアリングの結果生み出された面白いもの」は(自分が眺めてみたいばかりに、急遽 @GOROman さんにデモをお願いした) Oculus Rift や、○×な△□といったグッズです。そんな何かに興味がある人は、少し眺めてみると面白いと思います。
あるいは、そんなグッズを題材に、東京03がどんな即興コントを繰り広げるか…というあたりも、ちょっと楽しいかもしれません。
2013-11-16[n年前へ]
■空に流す灯籠で眺める「天上の消失点」 
知る限り「一番美しいプラネタリウム」が、また今年も始まりました。今晩は曇り気味な空なので、自然の星は見えなくて、月の明かりがたまに雲の向こうに伺うことができるだけです。けれど、たくさんの「人が天上に流す灯籠」が、街のいたるところから上がっていき、そんな人口の星空が頭上に拡がっています。... そんな景色を、iPhoneでチープに撮影して20倍速くらいの映像で眺めると、こんな風になります。
街中のそこらかしこから、頭上に向けて放たれていく灯りの軌跡を眺めていると、空の上に、天上の消失点があるように見えてきます。コムファイに自分の名前を描き・願いを込めて空に流すと、願いが成就すると言います。天上に位置するただ一点の消失点に向けて、祈りを込めて放たれたコムファイ(灯籠)が流れ集まっていきます。
2013-11-17[n年前へ]
■ヘリウム風船に「夢や希望」を乗せて・叶えるために飛ばします!? 
 2013年、チェンマイのロイクラトンで、空に流されていくコムファイ・コムローイを眺めてみると、一昨年2011年には見かけなかった「変わり種コムローイ」を見つけました。…それは、いくつかのヘリウム風船にぶら下げられ空高く上がっていくクラトン(灯籠)です。川面に浮かべ・流されていくはずの灯籠が、ヘリウム風船にぶら下げられて、どこか遠くの空に飛ばされているのです。
2013年、チェンマイのロイクラトンで、空に流されていくコムファイ・コムローイを眺めてみると、一昨年2011年には見かけなかった「変わり種コムローイ」を見つけました。…それは、いくつかのヘリウム風船にぶら下げられ空高く上がっていくクラトン(灯籠)です。川面に浮かべ・流されていくはずの灯籠が、ヘリウム風船にぶら下げられて、どこか遠くの空に飛ばされているのです。
 軽量化のためにプラスチックで作られたクラトン(灯籠)が、ヘリウムを詰めたゴム風船にぶら下げられ浮かんでいるのを見ると、「伝統の作り方とか関係なくて、何でもありだ!」と何だかとても楽しくなります。
軽量化のためにプラスチックで作られたクラトン(灯籠)が、ヘリウムを詰めたゴム風船にぶら下げられ浮かんでいるのを見ると、「伝統の作り方とか関係なくて、何でもありだ!」と何だかとても楽しくなります。
そしてまた、ヘンだけど奇妙に可愛い(まるで熊本県PRマスコットキャラクターのくまもんみたいな)「顔模様」のコムファイが屋台にたくさん吊され並んでいたりします。こうした色モノ系キャラクタたちも、普通の伝統的コムファイやコムローイと同じように、希望や夢を積んで空に飛ばされていくのです。
 コムファイに希望を積み込み・天に届け・望みを叶えるためには(コムファイへの)「サイン」が必要なので、空から地上に降ちてきたコムファイを眺めてみれば、そこには夢を望んだ人たちの名前が描かれていたりします。それは、まるで「空に浮かべられた絵馬」のようで、少し切なく・懐かしくなります。
コムファイに希望を積み込み・天に届け・望みを叶えるためには(コムファイへの)「サイン」が必要なので、空から地上に降ちてきたコムファイを眺めてみれば、そこには夢を望んだ人たちの名前が描かれていたりします。それは、まるで「空に浮かべられた絵馬」のようで、少し切なく・懐かしくなります。
2013-11-19[n年前へ]
■「安全・品質」のためにかける「コスト」 
 車の急加速事故に関する記事を読み、品質や安全性を上げるために「コストをどの程度費やす」ものだろうか?と考えました。何か「とても常識っぽいこと」「みんな常識的に知っているのだろう」というのようなことを、今日はふと考えました。
車の急加速事故に関する記事を読み、品質や安全性を上げるために「コストをどの程度費やす」ものだろうか?と考えました。何か「とても常識っぽいこと」「みんな常識的に知っているのだろう」というのようなことを、今日はふと考えました。
品質や安全性を高めるための作業やコストを費やすと、(品質や安全性が上がる結果)問題が生じることにより失われる「損失の量」が単調に減少していく・・・という右上図に描くような関係が、(非常に単純化されてはいますが)よくありそうなモデルに思えます。こういったモデルで「どの程度のコストをかける」のが適切なのでしょうか?
品質や安全性を上げるためにコストを掛けると「問題による損失」は低減していきますが、あまりにコストを掛けすぎると、(品質・安全性を高めるためのコストを全くかけなかった場合の)「問題による損失の最大量」を作業コストが上回ってしまいます。さすがに、これでは本末転倒でしょうから、いくら何でもそこまでコストを掛けるのはムダそうです。
 となると、「問題による損失」と「品質や安全性を上げるためのコスト」の和が最小になる状態というのが、「品質や安全性を上げるための適切なコスト量」ということになるのでしょう。そんな図(右図)を「品質や安全性を上げるためのコスト=x」「問題による損失と品質や安全性を上げるためのコストの和=g(x)」を描いてみると、つまりは、d g(x) / dx == 0 となるとき「問題による損失」と「品質や安全性を上げるためのコスト」の和が最小になり、それが最適コストなんだろう・・・というように見えてきます。
となると、「問題による損失」と「品質や安全性を上げるためのコスト」の和が最小になる状態というのが、「品質や安全性を上げるための適切なコスト量」ということになるのでしょう。そんな図(右図)を「品質や安全性を上げるためのコスト=x」「問題による損失と品質や安全性を上げるためのコストの和=g(x)」を描いてみると、つまりは、d g(x) / dx == 0 となるとき「問題による損失」と「品質や安全性を上げるためのコスト」の和が最小になり、それが最適コストなんだろう・・・というように見えてきます。
d g(x) / dx == 0 ということは、「(作業量に応じた)問題による損失量=f(x)」とすると d f(x) / dx >= -1 ・・・つまり、単純に、「品質や安全性を上げるためのコスト」を掛けても「問題による損失の減少」がそれに値する程度でなくなってしまうということを言ってるに過ぎません。
 それでは、この「(作業量に応じた)問題による損失量=f(x)」の形状が未知だったらどうすれば良いのかとか、これらのグラフの縦軸に「生み出される価値」も足し合わせてみたらどうなるか・・・とかいったことを、あるいは、原子力発電やありとあらゆる工学の産物に関したことを、暇な時にラクガキスケッチでもして考えを巡らせたくなります。
それでは、この「(作業量に応じた)問題による損失量=f(x)」の形状が未知だったらどうすれば良いのかとか、これらのグラフの縦軸に「生み出される価値」も足し合わせてみたらどうなるか・・・とかいったことを、あるいは、原子力発電やありとあらゆる工学の産物に関したことを、暇な時にラクガキスケッチでもして考えを巡らせたくなります。
2013-11-21[n年前へ]
■マダガスカル象鳥の卵10kgなら、卵1個から「卵焼き83人分」が作れます!? 
 「数値でみる生物学(生物に関わる数のデータブック)
「数値でみる生物学(生物に関わる数のデータブック)」を読んでいると、カイチュウの染色体数が「たった2個!」だとか、ゾウの妊娠期間が660日(2年弱!)といった、驚くべき・面白い数字が並んでいます。そんな数値の中に、マダガスカル象鳥の卵は「重量が10kg」というものがありました。…10kgと言われても、何だか実感が沸きません。そこで、日常の生活で食べる「鶏の卵」の大きさを基準にして、マダガスカル象鳥の卵の大きさを体感してみることにしました。
 M サイズの卵は「パック中の鶏卵1個の重量が58グラム以上、64グラム未満であるもの」となっています。つまり、一個約60グラムです。ということは、10kgのマダガスカル象鳥の卵なら(通常の鶏卵基準にすると)167 個分になります。たとえば、卵焼きを「鶏卵2個/1人前」で作るなら、(マダガスカル象鳥の卵1個から)83人分の卵焼きを作れることになります。
M サイズの卵は「パック中の鶏卵1個の重量が58グラム以上、64グラム未満であるもの」となっています。つまり、一個約60グラムです。ということは、10kgのマダガスカル象鳥の卵なら(通常の鶏卵基準にすると)167 個分になります。たとえば、卵焼きを「鶏卵2個/1人前」で作るなら、(マダガスカル象鳥の卵1個から)83人分の卵焼きを作れることになります。
とはいっても、マダガスカル象鳥の卵で卵焼きを作るには、当然「それ相応に大きなフライパン」が必要になります。卵焼きの厚みを5mmくらいとして、卵の比重を大雑把に1グラム/cm^3としてみると、83人分の卵焼き(10kg)はおよそ直径160cmくらい。
…といった、「数値でみる生物学(生物に関わる数のデータブック)」を眺めていると、色んな想像をしてみたくなります。
2013-11-22[n年前へ]
■Rasberry Pi に個人・教育用 Mathematica が無料添付 
 Rasberry Pi に個人・教育用 Mathematica が無料添付されるという話が出ていたので、早速Rasbian(Rasberry Pi) にMathematica をインストールして・動かしてみました。
Rasberry Pi に個人・教育用 Mathematica が無料添付されるという話が出ていたので、早速Rasbian(Rasberry Pi) にMathematica をインストールして・動かしてみました。
「バージョン 10.0 for Linux ARM 32 bit」というバージョン表示の Rasbian (Rasberry Pi)向けMathematica を動かしてみると、通常のデスクトップPC(OS)向けと同じように動作します。Wolfram Mathematica の優れた天は、言語としてのMathematica 言語と、思考整理環境としてのMathematicaノートブック、という2面がありますが、そのどちらも(通常のPC向けと同じように)使うことができます。それは、なかなかに魅力的です。
たとえば、Raspberry Pi Type A 256MBであれば、Amazonでも三千円台で買うことができたりしますから、自分専用のMathematica 計算カーネル・サーバや、フロントエンドをWEBアプリとして包み込んだサーバなどを立ち上げてみたりするのも、面白いかもしれませんね。


2013-11-25[n年前へ]
■「全10問の2択問題、デタラメな答で正解数5問以上の確率」は…!? 
 「全10問の2択問題、デタラメな答で正解数5問以上の確率」は…!?を書きました。この問題の面白い点は、「私たちの考え方・感じ方が、この問題に(なぜか)間違った答を返したがるのは、一体どうしてなのだろうか?」ということだと思います。
「全10問の2択問題、デタラメな答で正解数5問以上の確率」は…!?を書きました。この問題の面白い点は、「私たちの考え方・感じ方が、この問題に(なぜか)間違った答を返したがるのは、一体どうしてなのだろうか?」ということだと思います。
この問題で何より一番面白いことは、「私たちの考え方・感じ方が、この問題に(なぜか)間違った答を返したがる」ということ、そして「その理由は一体何なのだろう?」を考えてみても、その「正解」がなかなか見つからないことかもしれません。・・・あなたなら、一体どんな「理由・原因」だと考えますか?
2013-11-26[n年前へ]
■「共通一次」…改め「センター試験」の数学プログラム問題 
 かつて「共通一次試験」と呼ばれ、今は「センター試験」という名前で出ているらしき、大学入試のための問題を面白く読んでいます。各学科それぞれ24年分の過去問題を積み上げると、意外に分量があったり・今更ながら気づかされたりすることがあります。
かつて「共通一次試験」と呼ばれ、今は「センター試験」という名前で出ているらしき、大学入試のための問題を面白く読んでいます。各学科それぞれ24年分の過去問題を積み上げると、意外に分量があったり・今更ながら気づかされたりすることがあります。
驚かされたことのひとつが、最近の「センター試験」の数学問題の中には、プログラミング問題もあるんだ!ということです。行番号付きのBASICとか("GOTO"とか)何十年も前を思い出して懐かしくなります。
ちなみに、2004年度のセンター試験「数1A」第5問が下の写真です。「作られた目的・動作が不明なBASICプログラム」が登場して、「このプログラムの動きを答えろ!さぁ答えろ!」という問題です。…何だか、作者不明のプログラムをメンテする気分になり、「頼むから、もっとコメントをちゃんと書いてよ!」とか「もう少しインデントとか付けるなりしてもっと読みやすくして下さい…」とプログラム作者に毒づいたり・土下座して頼み込んだりしてみたくなります…。

2013-11-27[n年前へ]
■夕立(スコール)を降らせる雲の微速度撮影動画 

撮影した動画を眺めると、夕立(スコール)を降らせた部分の雲は消え去っていて、風に吹かれ移動してくる「雲の隙間」から太陽が微(ほの)かに照らしていることに気づかされます。そんな「雨が降って(地固まる…じゃなかった)雲が消える」なんて風景は普段気づきません。しかし、こんな風に通常比100倍くらいノロマに景色を眺めていると、普段気づかなかった景色を見つけることができたりもします。
意外に、いつもより「ずっと鈍い目」で景色を眺めてみると、なかなか気づくことができない面白いことを発見することができるのかもしれません。
2013-11-28[n年前へ]
■「太陽を中心に回る地球」が入った天球儀を眺めて「星座」を実感してみよう! 
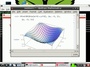
「○×月には△□星座が見える」とか「星座占いでは○×月生まれは△□星座になる」ということを実感してみたくて、「太陽を中心にして回る地球」が入った天球儀スケッチを描いてみました。つまり、24時間に1回クルリと自転する地球が、365日かけて太陽の回りを一周し、そして、その太陽や地球を回りで見守る「遙か遠くの星座」を描いてみました。
 こんな天球儀を眺めると、「夜=太陽がいる方向とは逆方向を向く時間」に見える星座が、1年365日かけて変わっていくことを実感できそうな気がします。たとえば、夏頃には、みずがめ座が太陽の反対側にいて、夕暮れ時に夜空に上ってくるんだなという風に見えてきたりします。あるいは、「太陽がどの星座と同じ方向に見えるか」ということを基準にして決められる「占いの星座」なら、夏頃の真反対・冬の時期に、太陽がちょうど水瓶座の方向に見えるから…そうか水瓶座は冬の誕生月の星座なんだな、と納得できたりします。そしてまた、北斗七星やカシオペア…北に向かう列車の名前が冠された北の空に浮かぶ星たちは、(日本北部からなら)夜ならいつでも見ることができそう…と感じられたりします。
こんな天球儀を眺めると、「夜=太陽がいる方向とは逆方向を向く時間」に見える星座が、1年365日かけて変わっていくことを実感できそうな気がします。たとえば、夏頃には、みずがめ座が太陽の反対側にいて、夕暮れ時に夜空に上ってくるんだなという風に見えてきたりします。あるいは、「太陽がどの星座と同じ方向に見えるか」ということを基準にして決められる「占いの星座」なら、夏頃の真反対・冬の時期に、太陽がちょうど水瓶座の方向に見えるから…そうか水瓶座は冬の誕生月の星座なんだな、と納得できたりします。そしてまた、北斗七星やカシオペア…北に向かう列車の名前が冠された北の空に浮かぶ星たちは、(日本北部からなら)夜ならいつでも見ることができそう…と感じられたりします。
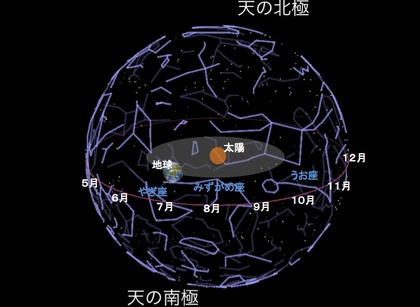
天球の手前側にある星座がひっくりかえるし、遠くにあるはずの天球が近いようにも見えます…。地球の夜側が昼に見えてしまいますし。地球を太陽の向こう側に置いて、天球の奥側を濃くして手前側を薄くするのはどうですか?
なるほど!それいいですね。どういう風にレンダリングのコードを書けば良いかを考えてみます! > ”地球を太陽の向こう側において、天球の奥側を濃くして手前側を薄くする”
2013-11-29[n年前へ]
■Raspberry Pi でUSB接続WEBカメラ画像をMathematicaで処理してみよう!? 
 Raspberry Pi にUSB接続のWEBカメラを繋いで、Mathematica で画像処理をさせてみました。USB接続のカメラの画像をMathematicaから直接読み込むのは面倒だったので、とりあえずfswebcamで画像ファイルとして撮影して、そのファイルをMathematicaに取り込む、という具合です。”Linux-ARM用には本関数は実装されてません”とエラーが返ってくる関数も多々ありますが、USB WEBカメラをRaspberry Pi に複数台繋ぎステレオマッチングさせて、距離マップを作成したりとか、色んな遊び方ができそうです。
Raspberry Pi にUSB接続のWEBカメラを繋いで、Mathematica で画像処理をさせてみました。USB接続のカメラの画像をMathematicaから直接読み込むのは面倒だったので、とりあえずfswebcamで画像ファイルとして撮影して、そのファイルをMathematicaに取り込む、という具合です。”Linux-ARM用には本関数は実装されてません”とエラーが返ってくる関数も多々ありますが、USB WEBカメラをRaspberry Pi に複数台繋ぎステレオマッチングさせて、距離マップを作成したりとか、色んな遊び方ができそうです。


2013-11-30[n年前へ]
■「スカートめくれ」を実現する…じゃなかった防ぐための屈み方講座 
「スカートめくれ」を実現する…じゃなかった防ぐための屈み方講座 を書きました。
女性の腰が2m/s^2 程度の加速度で動いていくのに対して、(それより遅れて)スカートが1.1m/s^2の加速度で下へ動いていく、ということは、女性の腰を基準にすれば、スカートが相対的に2 – 1.1 =0.8m/s^2の加速度で めくれ上がっていく…ということになります。だから、上の動画のように、スッと屈み込もうとした女性のスカートがフワリと浮かび上がってしまったわけです。