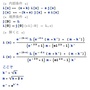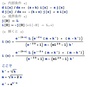hirax.net::Keywords::「酵母」のブログ

■「ビールの法則」で「白ビールの酵母・小麦タンパクの量」を見極めろ!?　

　地ビールの中でも、酵母や小麦蛋白が濾過されずにたくさん残っているビールは、それらの成分が（ビールを照らす）光を散乱させるため、白く淡い色に見えます。 だから、ヘーフェヴァイツェンビール（小麦酵母ビール）などは白っぽく色が淡く見えます。ビール内部で光散乱が生じると「白く見える」のは、照明光（白色光）がビール内部に入った後、ビール内部で光散乱が生じることにより、、ビール内の色素による光吸収が十分行われる前に（すなわちビールの色に色づく前に）、光がビール外部に出てしまうからです。 そういった光は白色のほぼ照明光そのままですから、ビールが白っぽく見えてしまいます。

　そんなヴァイツェンビールを見ながら、「ビールの色を見ただけで、酵母や小麦蛋白の量を判断できるか？」という話になりました。そこで、簡単な計算から「（単位体積あたりの）酵母や小麦蛋白の量」を求めるための方法を調べてみることにします。

　まず、簡単な思考実験から、ビール自体に色が着いていなければ、ビールの色からだけでは「（単位体積あたりの）酵母や小麦蛋白の量」は決められないだろう、ということがわかります。 なぜなら、ビールが完全に透明だったとしたら（全波長で光吸収がゼロだっとしたら）、ビール内部に酵母や小麦蛋白がたくさんあって、そこで光散乱がどれだけ生じようとビールから出てくる光は照明校と同じ白色光になってしまいます。ビールグラスの中（やグラスの向こうの景色）は不透明になりますが、「色」自体は完全に照明光と同じになってしまいます。

　また、ビールの色（たとえばビール内を光が単位長さだけ通過する際に行われる光吸収の量）がわかっていなければ、「ビールの色からだけでは光散乱の量（＝酵母や小麦蛋白の量）」はわからないだろう、ということもわかります。 なぜなら、たとえば、濃黄色のビールに酵母と小麦蛋白がたくさん入っていて、光散乱が多く生じることにより「薄黄色のビール」になったとしても、その薄黄色が「元から薄黄色のビールで、光散乱が全然ない（酵母も小麦蛋白も全然入っていない）」のか「濃黄色のビールが光散乱により薄黄色に見えている」のかを区別することができないからです。

　ということは、「ビール自体の色がわかっている」という条件下でのみ、「ビールの見た目の色（白っぽさ）から、光散乱の量（＝酵母や小麦蛋白の量）を求めることができる」という目処を付けた上で、その上で簡単な解析計算をしてみることにします。

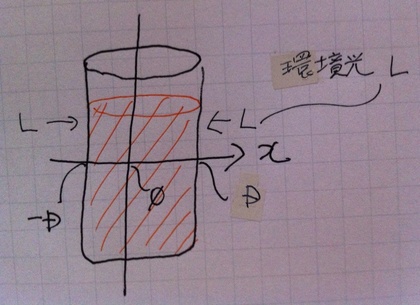
　まず、ビールグラス近傍にX座標をとり、グラス中央を原点とします。また、グラスの高さ方向・グラス回転方向はは無視します。 この時、x軸の正の向きに向かう光量をj(x)、X軸の負の向きに向かう光量をi(x)として、ビールグラスの界面での反射を無視すると、次のような連立微分方程式を書くことができます。 この連立微分方程式の内容はとても単純で「媒質中を移動する光は、進むに連れて光吸収されたり・散乱し進行方向を変えたりする」ということを書いたものです。

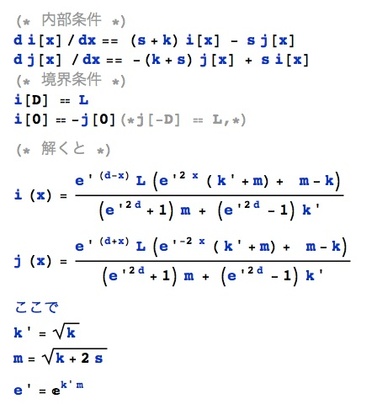
　連立微分方程式中で使われている変数、sは単位長あたりの（波長毎の）光散乱率で、kは単位長あたりの（波長毎の）光吸収率です。また、Dはビールグラスの半径で、Lは外部環境光です。

　この連立微分方程式は（連立微分方程式とはいっても）i(x)とj(x)は原点対称の「実は同じもの」ですから、結局のところ、普通の微分方程式です。そうした媒質内部の現象を書いた微分方程式に、ビールグラス境界で「外部からの環境光 L が入ってくる」という境界条件を付けて（あるいは、対称性から原点でi(x)とj(x)が等しいといった境界条件を付けて）、微分方程式を解いてやると、上に書いたようなi(x)とj(x)を表す式が導かれます。

　j(x)はビールグラスの右側に向かう（波長毎の）光量を示し、i(x)はビールグラスの左側に向かう（波長毎の）光量ですから、ビールグラスを外側から見た時の（光の波長毎の）光量はi(グラス半径）=j(-グラス半径）です。 すると、上で求められた解は、「ビールグラスを外側から見た時の（任意波長の）光量＝（波長毎の）ビール自体の光吸収率k　と （波長毎の）ビール自体の光散乱率 sの関数」という形になっていますから、（波長毎の）ビール自体の光吸収率kがわかっているならば、ビールの「色（任意波長の光量）」を観察すれば、「（光を散乱させている）酵母や小麦蛋白の量」がわかる、ということになるわけです。

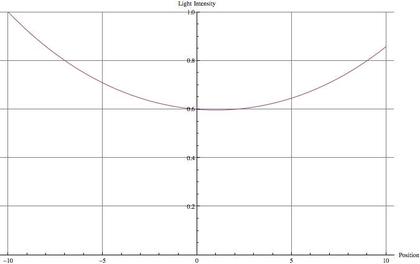　たとえば、右のグラフは（向かって）ビール・グラス右向きに向かう光量=j(x)を、微分方程式を解いた結果から示した一例です（横軸は位置, 縦軸は光量）。向かって左側はグラス外側から環境光が入射するため（右側に向かう）光量が多く、グラス右側では（主にグラス右側から入射した光が）散乱により方向を変えて・右側に進む光が一定量あることなどがわかります。

　しかし、私たちがビール・グラスを眺める時、「色」を感じることはできても、「任意波長の光量」といったものはあまり意識しないものです。そこで、次は、こうした媒質中の光吸収を計算する基本式「ランベルト・ベールの法則（Beer-Lambert law）」を使って、ビールの（見た目の）色と酵母や小麦蛋白の量）を具体的・体感的に眺めてみることにしようと思います。

　…何しろ、ランベルト・ベールの”ベール”はBeerですから、短く言ってしまえば「ビールの法則」です。「ビールの法則」なのですから、「白ビールの酵母・小麦タンパクの量」の見極めのために使わないと、何だかもったいないですよね？

■続「ビールの法則」で「白ビールの酵母・小麦タンパクの量」を見極めろ!?　

　「ビールの法則」で「白ビールの酵母・小麦タンパクの量」を見極めろ!?で、「酵母や小麦蛋白が濾過されずにたくさん残っているヴァイツェンビールの色から、酵母や小麦蛋白の量を見極めるための研究」を始めました。具体的には、「ビールの法則」ならぬ「ランバート・ベアの法則」と「ビールに溶け込んでいる色素の色（分光吸収率）」を使って、ビールグラスを外から眺めた色とビールに溶け込むことなく濁っている成分の量を結びつける式を導き出してみました。

　そこで今回は、導き出した「ヴァイツェンビールの濁り成分量と外見色の関係式」から、濁り成分量を変えた時（つまり濾過されずグラス中に残っている酵母や小麦蛋白の量が違う時）、ビールの色がどう違って見えるかを眺めてみることにします。

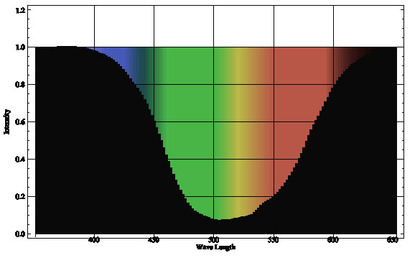　まず、ビールに溶け込んでいる（光を吸収しても散乱はさせない）成分の分光吸収率が右のような吸収スペクトルだとしてみます。「ビールといえば黄色」ですから、ほぼ黄色以外の波長の光を吸収するような特性です（グラフの黒領域が吸収される量を示しています）。

　そんな「黄色いビール」の中に含まれる濁り成分量を「全然入ってない~たくさん入ってる」まで９段階の条件下で、「ヴァイツェンビールの濁り成分量と外見色の関係式」を使って「ビールグラスの外見色（スペクトル）を算出してみると次のようになります。左上が濁り成分が全然入っていない状態で、右下がたくさん濁り成分がグラスの中に入っている状態です。

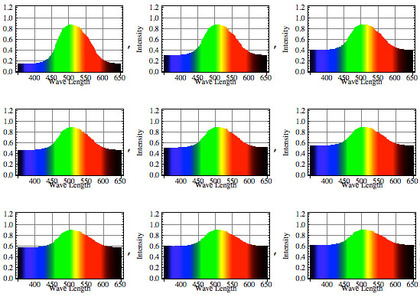
　「濁り成分」が全く入っていない条件では、青色や赤色の波長の光は多く吸収され、黄色近くの波長の光だけをビール外部に放出している＝綺麗な黄色に見えていることがわかります。

　それに対して、濁り成分が増えてくると「ビール内部で光が散乱され・青色や赤色が吸収されないままビール外部に出ていくために、どの波長の光も結構強く残っている＝白色に見える」ことが見てとれます。そして、その濁り成分の量と「ビールの白っぽさ」が対応していることも、（当たり前ですが）確認することができます（参考までにCIE Lab空間での色座標推移も右に貼り付けておきます）。

　こんな「ビール研究」を（ビールを飲みながら）していると、スマフォ・カメラでビールグラスを撮影するだけで、ビールの酵母・小麦タンパクの量…ありとあらゆるビールの特性を教えてくれるスマフォ・アプリなんていうものも、きっと近い将来には登場しているに違いない、という気がしてきます。

　作成した計算ノートブックはここに置いておきます。このノートブックは、以前作成した「色」を計算するためのMathematica用ライブラリの最新版です。また、このライブラリには三次元構造の中で反射・屈折・散乱を行う「光」のスペクトル変化過程を計算するための機能も入っているので、その機能を使って計算・解析してみるのも面白いかもしれません。