■ビックエッグの力学 
ドームを支える空気圧の謎
この回は(トンデモ話)であり、中途半端であるのだが、反省を込めてこのままにしておく。直すのが、面倒くさいわけではないので、念の為。
日本シリーズ'99をやっている(いた)。私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。そういえば、今年はドーム決戦である(だった)。ドームといえば元祖「東京ドーム」だろう。「東京ドーム」のWEB
- 株式会社東京ドーム (http://www.tokyo-dome.co.jp/about/index.htm )
| 東京ドームは、空気膜構造によるエアドーム。つまり内部気圧を外気より0.3%高くして、400トンもの超特大楕円形の屋根を膨らませるのがドーム建築のポイントなんだ。 ところで、この気圧差0.3%は、ビルの1Fと9Fぐらいの違いがある。とはいえ中と外の違いを体感することはほとんどない。 |
たった、0.3%の空気圧の差で400トンを支えるとは、ものスゴイ。すぐには納得できない数字である。別に疑い深い私でなくても不思議に思うことだろう。
そこで、確かめてみることにした。まずは、東京ドームの面積をx(m) * x(m)としてみる。すると、持ち上げることのできる重さ(トン)は、
- 0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x / 1000(kgからトンへ)* 9.8(Nから重力へ)
と計算できる(この式には実は間違いがある。詳細は後で...)。その結果を示してみる。
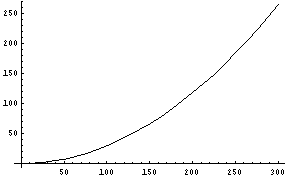 |
先の、Webから東京ドームのサイズを見てみると、x = 180mである。すると、持ち上げられる天井の重さは100トン程度であるということになる。おやおや、先の「400トンの天井を持ち上げる」というのとはずいぶん違う。これでは、天井を支えきれない。
 |
そこで、高さによる大気圧の差を導入し、天井近くの高い場所では「外部の気圧が低い」という条件を導入してみる。0.3%というのは地上での比で、天井のある上空ではさらに差があるとしてみるのだ。うーん、強引である。
さて、ここから後は(実は前も)トンデモ話になっているので眉に唾をつけて読んで欲しい。それを指摘して下さった、読者からの手紙への返事(とほぼ同じ内容)を下に示しておく。
青木さんへの手紙> 高さによる圧力の差は、高さの異なる二点間に存在する空気> の重さに見合ったものです。したがって、ドームの内部でも> 高いところほど圧力は低くなっている筈です。 その通りだと思います。WEB中で「うーん、強引である。」と書いたのはまさにその理由です。 それにも関わらず、強引な論法を続けたのは、文章の最後に「謎は解けないのに、東京ドームは存在している。 少し、くやしい。 」と書いた理由と同じです。まるで、「宇宙人が水道橋の駅前駐車場にUFOを停めて、サラ金に入って行くのを目の当たりにしている」ような、気持ちなのです。くやしいと強引になるのです。あぁ、何て人間らしいのでしょうか... また、計算をしていた時に少し勘違いをしていました>もし、ドームの内外の温度が等しければ、地上でも天井でも内外の差圧は>同じになるはずです。と仰るとおり、差圧は等しいわけですが、それを0mにおける大気圧に対するパーセンテージに直すと、高度が高くなればなるほど、そこの気圧に対してはパーセンテージは高くなります。計算をしていた時にその「パーセンテージが高くなる」ことを「差圧が高くなる」ことと同じに扱うという間違いを犯してしまいました。もちろん、基準の気圧が小さくなっているので、パーセンテージが高くなっても本当は差圧は変わらないわけです。「考えることを手抜きしていた」と言ってもよいかもしれません。要反省です。>ドーム内の温度が高ければ空気の密度> が減少し、天井の位置での差圧はより大きくなり、天井を支> えるのに有利に働きます。これは、浮力によって天井が持ち> 上げられていると考えても同じ事です。> という訳で、ドーム内外の温度差が逆転する夏と冬とでは天> 井を支えるのに必要な圧力を変えなければならないと思うの> ですが本当はどうなんでしょうか。 これは面白そうですね。そういえば、学生時代に地殻物理学を専攻していたのですが、夏と冬の大気圧の違いから、地殻歪の大きさに関係づけて、地震の予言をするなら、「冬に発生する」といった方が良い、話(もちろんかなり冗談で)をしていた先生がいました。その先生に「今回のトンデモ話」がばれたら、大目玉をくらうこと間違いなしです。 ビックエッグの謎は深まるばかりです。それでは、また。------------------------------------------------------------------ch3coohさんへの手紙> > >12/(100*100)*1000= 1.2g/cm2となります。> > >> > >地上での大気圧は約1Kg/cm2なので、上の値は> > >1.2%程度となり、 ここが疑問だったのですが、これは1.2%でなくて、0.12%ですね。なるほど、0.3%よりも小さいですね。実に納得です。 さて、他の方からの指摘もあり、私の計算には> >0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x > / 1000(kgからトンへ) * 9.8(Nから重力へ)> に1013(標準気圧 hPa)がかかっていないことが気になりました。 という間違いがあることがわかりました。全てはここが原因だったようです。 全ての疑問が解決しました。いやぁ、お恥ずかしい。また、他にも色々と面白い情報ありがとうございます。
ひとつわかったことは、間違いをすると読者からの手紙が沢山来るといううれしくもつらい事実であった。ここから、あとは封印したい思いで一杯なのだが、自戒を込めてこのままにしておく。しつこいようだが、直すのが面倒なのではない。
それでは、高さによる大気圧の差を計算してみる。理科年表から15℃の「標準大気の場合の高さと気圧の表」を見てみる。 ちなみに、東京ドームの温度は、「ガス熱源による冷暖房システムにより、夏期は28℃の冷房、冬期には18℃程度の暖房が行われている」とある。今回の計算は外気の温度が15℃で、内部は冬期には18℃程度の温度に調整されているものとしておこう。
標準気圧は海抜0mで1013mbであり、200mでは989.5mbである。理科年表が古いのでPascal値でなく、mb表示になっている。
これから、1m当たりのmb変化を計算すると、0.12mb/mとなる。比率に直すと、0.012%/mということになる。例えば、「ビルの1Fと9Fぐらい」の高さの差は30m位であろうから、それを大気圧の比に直すと、99.6%位となり、先の記述と大体合う。
以下に、高度に対する大気圧の差(の比 %)を示してみる。
 |
このグラフで30mの場所を見てみると、99.6%位というわけだ。これが、先のWEB上の「この気圧差0.3%は、ビルの1Fと9Fぐらいの違いがある。」という説明と合うわけである。
次に必要なのはドーム外部と内部の大気圧の比から、力に直してみる。基準面からの高さ0mにおける気圧を1hPaとして、1hPa = 10^2 N/m^2 = 10^2 m^-1 kg s^-2という単位換算を使うと、持ち上げることのできる重さは、
- (100-大気圧の差(の比 % )) / 100(%から単なる比へ) *9.8(重力に換算) / 1000(kgからトンへ)* 100(hPaからN/m^2へ) * x^2(ドームの面積)
東京ドームの高さは「グラウンド面から 61.69m」とあるので大雑把に100mとしてみる。
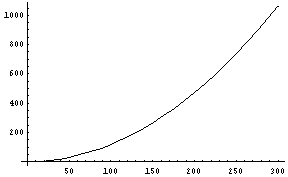 |
この計算結果によれば、東京ドームのサイズを180mとした時には、「持ち上げることのできる力」は400トン位になっている。ということは、先のWEBの記事と大体一致するわけである。
しかし、この計算では致命的な欠陥がある。天井の高度が低いときには、400トンを持ち上げるためにはもっと高い「ドーム内部の圧力を必要とする」ことだ。
例えば、0.3%空気圧の差の条件で、「天井の高度」に対する「持ち上げることのできる力」を計算してみると、次のようになる。
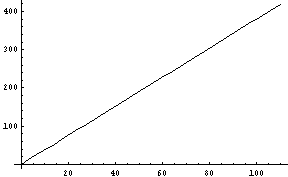 |
これでは、天井の高さが下がるとますます天井の重さを支えきれなくなってしまう。それに、そもそも天井をどうやって持ち上げたのだ?屋根を持ち上げるインフレートという作業はどうやって行ったのだろう?
今回の計算は謎が増えただけかもしれない。謎は解けないのに、東京ドームは存在している。
少し、くやしい。