2011-01-25[n年前へ]
■「分数階微分」「半端(ハンパ)階微分」…どんな名前が好きですか!? 
 最近、私の周囲若干1メートルの近世界では、数学が大ブームになっています。だから、たとえば、「ノルム空間のすべてのコーシー列がその空間中に極限を持つとき」と口ずさめば、その奇々怪々で意味不明な呪文を聞いた人は、すぐさま「その空間は完備"completeness"であり、バナッハ空間"Banach space"とよばれる」と一気に答えなければならない、と暗黙のルールがあるくらいです。
最近、私の周囲若干1メートルの近世界では、数学が大ブームになっています。だから、たとえば、「ノルム空間のすべてのコーシー列がその空間中に極限を持つとき」と口ずさめば、その奇々怪々で意味不明な呪文を聞いた人は、すぐさま「その空間は完備"completeness"であり、バナッハ空間"Banach space"とよばれる」と一気に答えなければならない、と暗黙のルールがあるくらいです。
そんなマイリトル数学ブーミングな雑談中で、なぜか「分数階微分」の話題になりました。それは、「分数階微分」の「分数階」は他の名称の方が混乱しなくて良いのではないか…などという、役にも立たないそうもない楽しい雑談です。
関数f(x)をフーリエ空間でF(w)と表すとき、f(x)のn階微分は(iw)^n F(w)と表される。「n階微分」と書くと、まるでnは整数であるかのようですが、この「分数階微分」における「n階微分」のnは分数=有理数に限る必要もなければ、実数に限る必要もない・・・となれば、「分数階微分」の「分数階」という名付けを少し考え直したくなります。
Fractional Derivatives
 "分数階微分"="Fractional Derivatives"のFractionalに、"分数"=有理数という意味を感じてしまうと、何だか少しわかりにくくなるかもしれません。むしろ、そこからは、”半端(ハンパ)な”という実に中途半端な意味を感じた方が、むしろわかりやすく、楽しいような気もします。
"分数階微分"="Fractional Derivatives"のFractionalに、"分数"=有理数という意味を感じてしまうと、何だか少しわかりにくくなるかもしれません。むしろ、そこからは、”半端(ハンパ)な”という実に中途半端な意味を感じた方が、むしろわかりやすく、楽しいような気もします。
「分数階微分」の代替ネーミングを考えるとしたら、どんなものになるでしょうか?「分数階微分」「半端(ハンパ)階微分」、一体全体、どんな名前が自然に感じるものでしょうか。・・・こんな話題が楽しそうに思えたならば、街を歩きながら、こっそりこんなフレーズを口ずさんでみましょう。「ノルム空間のすべてのコーシー列が・・・」、きっとそのとき、あなたの横を駆け抜ける人が、「その空間は完備であり・・・」と答えてくれるはずです。
2014-10-05[n年前へ]
■画家が使った「色」を「距離」にした「画家の空間」を描いてみよう!? 
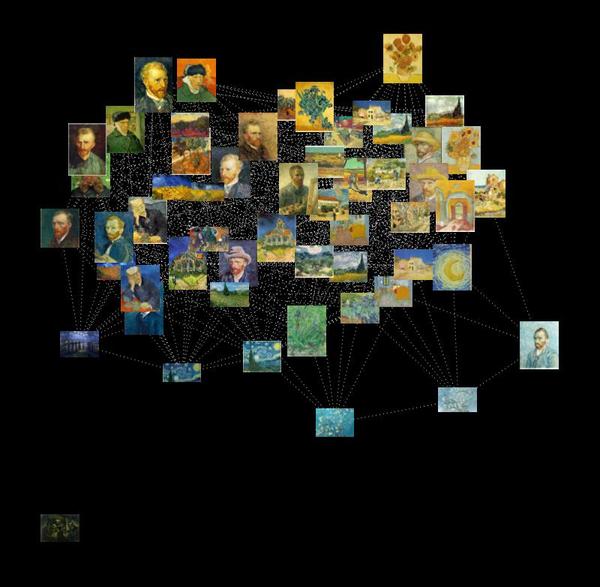
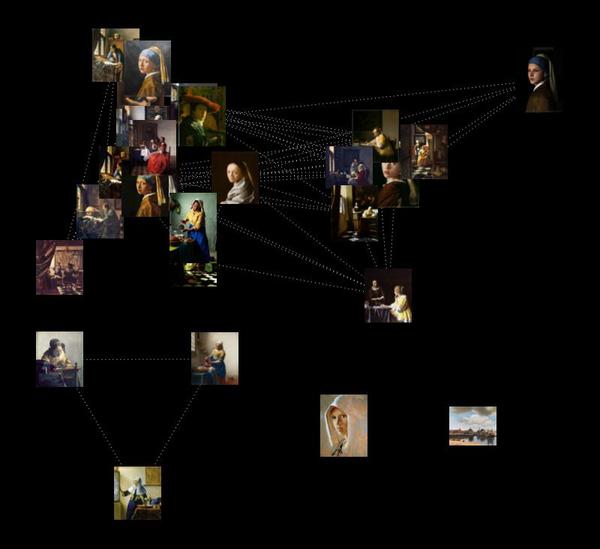
昨日は、画家の「代表色」を当てる目(色)利きゲームをしてみたので、今日は画家の代表作をGoogle画像検索で収拾し、それら名画に使われている使用色を「距離」として、つまりは色空間での距離をものさしにして、画家の「地図」を描いてみました。
そんな色空間を眺めてみると、たとえばゴッホが描いた絵画の色空間を眺めてみると、左(上)の領域、つまり、緑(や赤)を主体にしたものよりも、それ以外の青や黄色の世界が「眩しい昼」や「星輝く夜」っぽくて好きだなと、自分の好みを感じたりします。
あるいは、フェルメールの絵画を集めた世界地図を眺めると、…使われている色の違いというのか、あるいは、その明るさ・鮮やかさの違いというのか、北向きの窓から室内に差し込む光を頼りに描かれた絵はぼんやりとしていて、明るさが足りない日本海側の冬景色…に見えてきたりします。
ちなみに、「ゴッホの世界地図」を作ってる途中の計算動画は、下のような感じ。まるで、ゴッホの絵画たちがみんなでダンスを踊ってる感じ。マティスが描いた絵画で眺めてみるのも結構面白いかも。

2016-12-23[n年前へ]
■Python/OpenCVで画像多重解像度解析コードを書いてみる 
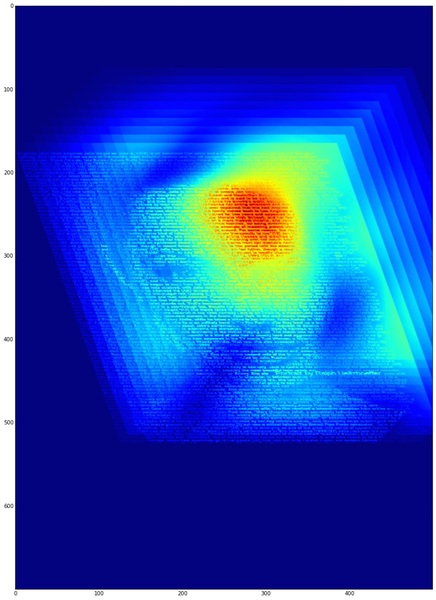 多重解像度解析…といっても直交基底に分解するというような話ではなくて、単に各周波数帯の特性がどの程度含まれるかを眺めるといった用途なら(つまり、ガボール変換やSTFTを掛ける感じの程度の用途なら)、Python/OpenCVを使って十数行で書けるかも?と思い書いてみました。もちろん、実装は簡単第一最優先!というわけで、ガウシアンフィルタ差分で2次元のバンドパスを作成し、それを周波数軸で重ねて眺めてみるというくらいの話です。
多重解像度解析…といっても直交基底に分解するというような話ではなくて、単に各周波数帯の特性がどの程度含まれるかを眺めるといった用途なら(つまり、ガボール変換やSTFTを掛ける感じの程度の用途なら)、Python/OpenCVを使って十数行で書けるかも?と思い書いてみました。もちろん、実装は簡単第一最優先!というわけで、ガウシアンフィルタ差分で2次元のバンドパスを作成し、それを周波数軸で重ねて眺めてみるというくらいの話です。
実際に書いてみたら、ポスト処理含めて約20行くらいになりました。超入門的な画像処理コードですが、1次元〜2次元の多重解像度解析や周波数解析を行うことは意外に多いような気もするので、適当に貼り付けておくことにします。*
*画像処理クラスタからのコメント:
・マルチスケールで眺めるなら、DCゲイン1同士のガウシアン差分をとり、そのL2ノルムを1に正規化しすべし。
・周波数軸は等比的にした上で、ボリューム的表示も等比的比率で重ねたい。
import numpy as np
import cv2
from matplotlib import pyplot as plt
def DOG(img, s, r):
img2=img.astype('uint16')
img2=img2*128+32767
gs = cv2.GaussianBlur(img2,(0, 0), s)
gl = cv2.GaussianBlur(img2,(0, 0), s*r)
return cv2.absdiff(gs, gl)
img = cv2.imread("sample2.jpg",0 )
(h,w)=img.shape
pts1 = np.float32([[0,0],[w,0],[w,h],[0,h]])
pts2 = np.float32([[0,h*1/4],[w*3/4,h*1/4],
[w,h*3/4],[w*1/4,h*3/4]])
M = cv2.getPerspectiveTransform(pts1,pts2)
baseImg = cv2.warpPerspective(
img.astype('uint16'),M,(w,h))
for i in range(100,5,-10):
pts1 = np.float32([[0,0],[w,0],[w,h],[0,h]])
pts2 = np.float32([[0+i,h*1/4-i],
[w*3/4+i,h*1/4-i],[w+i,h*3/4-i],[w*1/4+i,h*3/4-i]])
M = cv2.getPerspectiveTransform(pts1,pts2)
img2 = cv2.warpPerspective(DOG(img, i, 1.05),M,(w,h))
baseImg = cv2.addWeighted(baseImg, 0.9, img2, 0.3, 0)
plt.figure(figsize=(6,6))
plt.imshow(np.array(baseImg))
plt.autoscale(False)



