2010-04-12[n年前へ]
■拡散方程式で考える「あみだくじ空間」と「空間ワープ」 
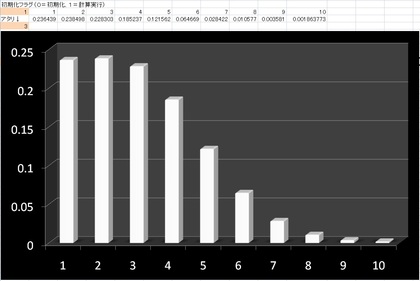「あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる」で、あみだくじの（平均的な）動き方を１次元の拡散方程式で解き、アタリを引く確率分布を考えてみました。
そのことに関して会話をしている中で、「とても新鮮で、着想が面白いな」と感じることがありました。そのアウトラインはいずれ平易な形で紹介させて頂くこととして、ここでは、マニアックで一般受けしそうにない部分を、マニアックで一般受けしそうにない記述で、そのとても面白かった話題を書いてみようと思います。
といっても、hirax.netを読みに来る人は、これすなわち、一般的ではないとってもニッチ（≠リッチ）な変わりものであるわけですから、そういった方には、ちょっと面白いのではないか・楽しめるのではないか、と思います。
前回紹介したように、あみだくじのアタリの場所がわかっている時には、その（平均的な）動き方を１次元の拡散方程式で解くことで、（平均的には）ここがアタリやすい場所だ、ということを求めることができます。アタリの場所が中央でなく、横線が十分にたくさんある場合には、アタリが左に寄っているなら左端、アタリが右に寄っているなら、右端がアタリやすい場所になります。横線の数が少なく、アタリが端にそれほど近くない場合には、アタリの真上がアタリの確率が高くなります。
端っこが確率が高くなるのは、両端がノイマン条件になっていて、両端で折り返される部分多重に重なるから、ということになります。部屋の中のゴミの動きをランダム・ウォークで考えたとき、四隅にゴミが滞留しやすいのと同じ具合です。
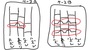
そんな話をしているとき、「じゃぁ、こんな線を引いたら？」「あるいは、こんなのは？」と言いながら、下図のような２つのケースのあみだくじ（の横線）を引かれました。…これは、ちょっと、とても面白い新鮮で面白い着想だと思いませんか？ 確かに、そういう線を、私たちはよく引きます。けれど、そういうことを、年を経るうちに、いつの間にか忘れてしまっていたことに気づかされました。
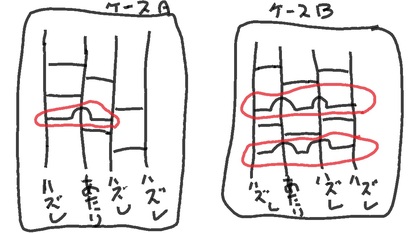
ちなみに、上図のケースＡのような場合、あみだくじを表現した１次元の拡散方程式で言うと、拡散の速さが速くなることになります。短い時間（あみだくじで言うなら、縦方向の距離で）で、アタリの場所が遠くまで移動していくことになります。つまり、遠くと遠くの空間を結び付ける、これは一種の”ワープ”する線です。
そして、上図 ケースＢの場合には、左右の両端が、「ノイマン条件」でなく、「周期境界条件」に（線の数がある分だけ）変化していきます。この場合も、結局は、一種の”ワープ”する線であって、それが空間の「反対側」どうしを結び付けている、という具合です。
結局、これらの”縦線をまたぐ”ような線は、離れた場所を強引に結びつけ、その空間どうしを”ワープ”できるようにすることで、隣り合った空間にさせてしまう、という恐ろしい効果をもっていることを、その当たり前のことを、空間内の拡散現象を表現する拡散方程式を解く、ということをする中で眺めると、ことさらに強く印象付けられます。
拡散方程式で考える「あみだくじ空間」と「空間ワープ」…何だか、そんなことを考え始めると、ルイス・キャロルの「不思議の国のアリス
この話題、もう少し、続きます。
だってそうでしょう？箱は開けてみなきゃ、中身はわからない。電話は出てみなきゃ、相手はわからない… 少なくとも、旧式の電話はね。
人の心だってそうよ。…こうして…ノックしてみないと、わからないの。
加納朋子「螺旋階段のアリス」
2010-04-13[n年前へ]
■拡散方程式で考える「あみだくじ空間」と「（見えない）時空間ループ」
拡散方程式で考える「あみだくじ空間」と「空間ワープ」の続きです。前回は、”縦線をまたぐ”ような線が、離れた場所を強引に結びつけ、その空間どうしを”ワープ”できるようにすることで、隣り合った空間にさせてしまう、という何やら不思議な存在であるのかもしれない、ということを考えてみました。
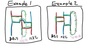
それでは、次は、こんな場合ならどうしたら良いでしょう？今度は、横線同士が交差していたり(下図のExample1)、同じ縦線同士を繋ぐ線があるような場合(下図のexample2)です。
あみだくじを拡散方程式で解くときには、縦線の「横方向」が「空間」を意味します。それに対して、「縦方向」はすなわち「時間」を意味することになります。「横線同士が交差する」ということは、異なる縦線の間で「時間」が共通のものでなくなってしまう「奇妙な線」であるように思えますし、「同じ縦線同士を繋ぐ線」はまるで過去や未来へ「タイムトリップ」する「不思議な線」に見えます。
今回考えてみたいのは、こういったスペシャル技を、ちまり時間軸を捻じ曲げるような「線」をどう扱うか、ということです。「どう扱うか」というのは、「どう考えると、単純に思えるか」ということです。「単純で共通なルールで記述できるか、と言い換えても良いかもしれません。
なぜかというと、この「線」について考え出すと、少し「スッキリしない」というか「気持ちが悪い」ことが出てくるからです。具体的には、「どの経路を考えてみても、通らない線がある」とか「横線に対して、（両方向に進む経路があって欲しいのに）片方向に進む経路しかない」、あるいは、「線を追いかけていくと、下から上に遡らなければいけない部分がある」ということです（下図参照）。
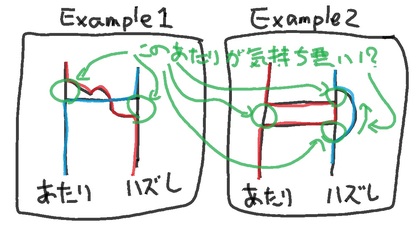
この「時空間を歪ませるようなスペシャル線」は一体どう扱う・どう考えれば良いのでしょうか？そんなに考え込むことでもないのかもしれませんが、あみだくじというものを考えるとき、「通らない線がある」「横線に対して、（両方向に進む経路があって欲しいのに）片方向に進む経路しかない」「線を追いかけていくと、下から上に遡らなければいけない部分がある」というのは、あまりに「おさまりが悪いこと」であるように思われます。
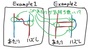
そこで、こう考えてみることにしました。下図のように、時間を捻じ曲げるているような線の部分には実は「縦線が隠されている（そういう仮想縦線を考えてみる）」と考えてみるのです。そして、その（仮想）縦線は最下部と最上部が繋がっていて、最下部からさらに下にさがると…アラ不思議、最上部にワープして、そこから下に降りていく、という具合に考えてみるのです。それが、下の図です。
すると、例外的な現象に思えていた不思議なことが、ごく当たり前の普通のあみだくじに見えてきます。あみだくじを辿る線は、いつでも下方向にしか移動しません、つまり、「線を追いかけていくと、下から上に遡らなければいけない部分がある」という現象は消えますし（仮想線の最下部でも、（仮想線の最下部と最上部が連結されているだけで）その空間上は下に落ち続けているのみです。）、「（いろいろな経路を考えたとき）通らない線」というものもなくなりますし、「横線に対しては、両方向に進む経路が必ずある」という、ごくあたりまえのあみだくじに思えてきます。（下図参照）
というわけで、横線同士が交差していたり、同じ縦線同士を繋ぐ線がある時には、そこには実は見えない縦線が隠されていて、その縦線はたとえるなら上下両端が繋がったことで「明確な端を持たない」ということだけが特殊だ、と考えてみるのです。「実は目には見えづらい空間（縦線）があり、そこでは時間軸は永遠のようでなぜかループしている」というわけです。
こんな風にあみだくじを、あみだくじの「スペシャル線」から考えてみると、何だか不思議なくらい惹かれます。そして、考えていくうちに、変に思えていたものが、いつの間にか、ひとつの綺麗な星座のように見えてきます。それは、とても面白い感覚です。
数字がバラバラに書いてあって、その数字を順番になぞっていくと最後に絵ができる"Connecting Dot"ってパズルがあるじゃない？ バラバラだったりしても、途中で間違っているように思えたりしても、色々と続けていたら最後に何か浮かび上がってきたりしたら、それで良かったりするのかな？って時々思ったりするの。
種ともこ 「どこかの学園祭コンサートで」
（目の前にいる人・目の前にある悩みを）ボーと見ていると、おもしろいものが見えてくる。その面白いものが見えてくることを"コンステレーション"と呼びます。"コンステレーション"というのは「星座(を意味する言葉)」です。
河合隼雄 「河合隼雄 その多様な世界―講演とシンポジウム」
星が散らばっている時、その星を結んだ瞬間が一番楽しい。
浅草キッド 水道橋博士
2010-04-16[n年前へ]
■「あみだくじ無限ループ」を生み出す「（見えない）時空間ループ」
「なぁ、あみだくじで無限ループって作れるとおもうか？」という面白いスレッドを読みました。
なぁ、あみだくじで無限ループって作れるとおもうか？このスレッドの中では、結局、「終わらないあみだくじは存在しない」という結論になっています。
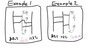
けれど、普通のあみだくじでなく、拡散方程式で考える「あみだくじ空間」と「（見えない）時空間ループ」で扱ったような、横線同士が交差していたり、同じ縦線同士を繋ぐ線があるような、普通ではないけれど「よくやりがちな」あみだくじなら、どうでしょうか。しかも、前回考えたように、そういう特殊線には実はゴールとスタート地点が繋がっている縦線が隠れているとしたら、どうでしょうか？たとえば、前回描いた下のような例です。
「ゴールとスタート地点が繋がっている縦線」があるとするならば、「終わらないあみだくじ」は存在する。けれど、そのスタート地点もゴール地点も表には出てこない（隠されている）からその存在を意識しないだけ、ということになります。具体的には、上図に緑色の線で描いた経路です。この経路は、「終わらない」「無限ループ」になっています。ただし、その経路は（あみだくじの参加者にはスタート地点が）見えない「仮想縦線」なので、その存在に気付かないだけ、という具合です。
横線同士が交差していたり、同じ縦線同士を繋ぐ線の後ろに「仮想縦線」が隠れていると考えてみると、あみだくじの「（スタート地点とゴールとの）一対一対応といった特性はそのままに（それ以外の特性も前回考えたようにそのままに）、「あみだくじの無限ループ線」が存在しうる、ということになります。
何だか、ちょっと面白いと思いませんか？
」など。