hirax.net::inside out::2010年04月08日

■あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる　

　あみだくじを作ったとき、「アタリ」がどのような分布になるかは、大雑把には、拡散方程式で解くことができます。もし、あみだくじに横線があれば、右へ行ったり・左に行ったり、酔った人がさまよい歩く酔歩（ランダムウォーク）のように「アタリ」を選ぶことができる場所が、推移するわけです。

　たとえば、拡散方程式を横軸を縦線感覚で離散化し、縦軸は…これまた適当に離散化し、縦方向単位長さ移動するときに、どれだけ左右への移動が生じるか（＝横線が縦線に対して、どの程度の頻度で存在するか）を考えてやり、そしてその離散化された拡散方程式を解いてやれば「あみだくじ」のアタリ分布を計算することができます。

　左端と右端の「境界条件」では、そこで「折り返されたような」動きをするわけですから、ノイマン条件を適用してやればよいことになります。また、時間ステップは、いつものように「循環参照による手動再計算」を用いて実現してやれば良い、ということになります。

　というわけで、エクセルでプロトタイピングして、作ってみたのが下の計算シートです（作成したエクセルシートはここに置いておきます）。たとえば、下のグラフは、アタリが左から３番目縦下部にあった場合に、一体、どの縦線を選ぶの良いかを示す確率分布になっています。今のこの状態なら、左から１番目、２番目、３番目が大体同じアタリ確率になっていて、もう少し細かく眺めてみると、左から２番目を選ぶのが一番アタリをひく可能性が高い、ということがわかります。

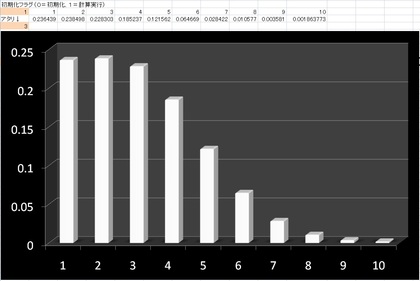
　上の例の場合には、一番アタリをひく可能性が高い線が、アタリのある真上より少し端側に寄りました。この「アタリをひく確率が高い線が端に寄る」傾向は、横線が多いほど激しくなります。…とはいえ、あみだくじを作る時のことを考えると、実際にはあまり横線の数が多くないように、つまり、手抜きあみだくじが多いように思います。

　そんな時は、手抜きあみだくじをするときは、アタリの真上近くを選び、そうでない場合にはアタリに近い端っこを選ぶ、というのが、あみだくじ方程式から導き出されるおトク知識と言えるのかもしれませんね。