hirax.net::Keywords::「循環参照」のブログ

■あみだくじシミュレーションをエクセルでプロトタイピングしてみよう　

　「電子ペーパー」でもあるエクセルは、プロトタイピングに向いている。と書いたので、今日は「あみだくじシミュレーション」をExcelで適当に書いて（描いて）みました。そうでした、私は自分自身で作ることが好きなのでした。

作成したエクセルのファイルは、ここに置いておきます。ワークシートの説明（あるいは修正）や、ワークシートを使って色々なことを考えてみよう、ということは明日以降にしてみようと思います。とりあえず、このエクセルのワークシートを実行しているところを動画キャプチャしたものが、下の動画です。

　このエクセル・ワークシートは、循環参照を使い、また計算順序を考慮したバッファリングを使うことで計算が成り立っています。ただし、エクセルの実装の仕組みのために、手動計算を行うためにF9を押しっぱなしにしても、反復計算が全セルに渡って行われるわけではないように思えます(これは検証していない未確認情報です）。そのため、計算を確実に行わせようと思うなら、今のところ、（あみだくじの横棒の数だけ）F9を連打する必要があります。

　あみだくじを考えるなら群論を使えとか、IF関数を使うのであればVBAを使うやり方と大して変わらないのでは？とか、エクセルでない他のプログラミング言語を使った方がよっぽど楽にプロトタイピングをすることができるのに…!?という感想も多々出てくるだろうと思います。

　とはいえ、今日はとりあえず、あみだくじシミュレーションをエクセルでプロトタイピングしてみました。（加減乗除だけで実現したのではない）つまらない実装ですが、（あくまで）暇なときに眺めて遊んで頂ければ、幸いです。

■あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる　

　あみだくじを作ったとき、「アタリ」がどのような分布になるかは、大雑把には、拡散方程式で解くことができます。もし、あみだくじに横線があれば、右へ行ったり・左に行ったり、酔った人がさまよい歩く酔歩（ランダムウォーク）のように「アタリ」を選ぶことができる場所が、推移するわけです。

　たとえば、拡散方程式を横軸を縦線感覚で離散化し、縦軸は…これまた適当に離散化し、縦方向単位長さ移動するときに、どれだけ左右への移動が生じるか（＝横線が縦線に対して、どの程度の頻度で存在するか）を考えてやり、そしてその離散化された拡散方程式を解いてやれば「あみだくじ」のアタリ分布を計算することができます。

　左端と右端の「境界条件」では、そこで「折り返されたような」動きをするわけですから、ノイマン条件を適用してやればよいことになります。また、時間ステップは、いつものように「循環参照による手動再計算」を用いて実現してやれば良い、ということになります。

　というわけで、エクセルでプロトタイピングして、作ってみたのが下の計算シートです（作成したエクセルシートはここに置いておきます）。たとえば、下のグラフは、アタリが左から３番目縦下部にあった場合に、一体、どの縦線を選ぶの良いかを示す確率分布になっています。今のこの状態なら、左から１番目、２番目、３番目が大体同じアタリ確率になっていて、もう少し細かく眺めてみると、左から２番目を選ぶのが一番アタリをひく可能性が高い、ということがわかります。

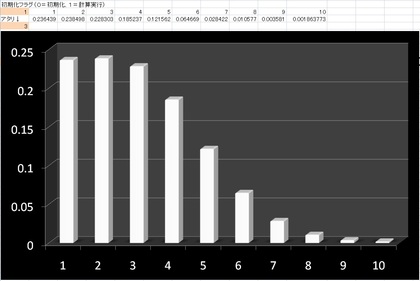
　上の例の場合には、一番アタリをひく可能性が高い線が、アタリのある真上より少し端側に寄りました。この「アタリをひく確率が高い線が端に寄る」傾向は、横線が多いほど激しくなります。…とはいえ、あみだくじを作る時のことを考えると、実際にはあまり横線の数が多くないように、つまり、手抜きあみだくじが多いように思います。

　そんな時は、手抜きあみだくじをするときは、アタリの真上近くを選び、そうでない場合にはアタリに近い端っこを選ぶ、というのが、あみだくじ方程式から導き出されるおトク知識と言えるのかもしれませんね。

■続　エクセルにおける循環参照時の計算順序　

　「エクセルにおける循環参照時の計算順序」で書いたような反復計算がおこなわれるのは、あくまで「循環参照」がされているセルに対してである。この「循環参照がされているセルに対して」ということは、えてして忘れてしまいやすい。つまり、シートの一部に「循環参照」がされているセルがあれば、シート全体が反復再計算されるのだ、という勘違いをしてしまいやすいように思う。

　反復計算がされるのは、あくまで「循環参照」がされているセルだけ、である。「循環参照」がされているセル群だけが反復計算の対象になり、それらのセル群の（前回計算結果との）変化量が所定値以下になるまで、それらのセル群に対して再計算を（前回記事のような順番で）行うことになる。

　シート上で「循環参照がされていないセル」に関しては、再計算されることはなく、初回の計算時の値がそのまま使われる。だから、たとえば、どこかのセルに乱数値を返すようなものが含まれていたとしても、つまり、計算ごとに明らかに変化するようなセルが含まれていたとしても、（循環参照がされていない限りは）そのセルの値は初回の計算で決まり、変化することはない。考えてみれば、当たり前の話だが、油断するとその当たり前を忘れてしまう。

　えてして、反復計算が行われる時には、シート全体が再計算されるという勘違いが頭の中に忍び込むことがある。そして、その間違った先入観のもとに、エクセルでプロトタイピングをしたりすると、思ったような計算がされず、ラピッド・プロトタイピング、すなわち、素早くたたき台を作とうと思ったはずなのに、多量の時間を費やす羽目になってしまったりする。

　エクセルの基本的な機能だけを、しかし、その基本的な機能を深く解説した本を読んでみたい。

■エクセルで飛び出す"立体"粒子群アニメーションを作ってみよう!?　

　21世紀に入った頃から、「表計算ソフトを使って、色んなシミュレーションをしてみる」ということをしています。いつも、夏になるとそんなことをしています。だから、暑い夏が来ると、いつもエクセルの勉強を”少しだけ”します。そして、いつもエクセルを憎み、一年くらいは触りたくなくなります。…けれど、憎みと愛は裏表、というわけで、結局エクセルに触り続ける毎日です。

　さて、そんな年中行事とは関係なく、昨日は「エクセルのグラフをマウスでグリグリ動かしながら赤青メガネで飛び出す立体動画で眺めよう!?」ということをしてみました。そこで感じたのは、エクセルは三次元的に眺める価値のあるグラフはなかなか作ることができない、ということでした。

　しかし、そんな風に限界を感じるときは、そこで感じる限界は多くの場合、自分の限界そのものである、ということもよく感じます。…というわけで、今日は、エクセルで粒子挙動シミュレーションを行い、その結果をアナグリフ立体動画として表示してみることにしました。

　そこで、まずは、（反復計算を用いて）簡単な「粒子挙動シミュレーション」をエクセルで行うことができるようにしました。そして、その上で、その粒子群の動きの計算結果を位置・大きさを（適当に）透視変換をした上で、散布図（バブルチャート）として、アナグリフ立体表示できるようにしてみたのです。そうすれば、左右視差による遠近感に加え、バブルの大きさが遠近に合わせた大きさで表示されることで、自然に立体感をもって眺めることができるわけです。

　その結果を、先日、作ったアナグリフ表示アプリケーションでアナグリフ立体動画にしてみた結果が、下に張り付けた動画になります。ムービーキャプチャーはいつものようにカクカクしてしまっていますが、もちろん、本当は、とても滑らかに動いています。というわけで、今日は「エクセルで飛び出す"立体"粒子群アニメーション」を作ってみました。