hirax.net::Keywords::「離散化」のブログ

■ Mathematica <-> Excel <-> Photoshop　

　社内で行われる予定のMathematica 講習会で何か話をしてみることにした。Mathematica <-> Excel <-> Photoshop の連携の話でもしてみようか。Mathematicaで方程式を離散化しエクセルのシートを作り、エクセルのシートからPhotoshopのプラグインが自動的に作られるとか、そんなネタでもやってみようか。それとも他のネタを考えようか…？

■Spectrum Color Conversion　

　Spectrum Color Conversion は分光的な色変換を行うことができるWEBページです。 Spectrum Color Conversion::RGBtoCMY はディスプレイで用いられているような赤・緑・青のRGB加算混色で示された色（スペクトル）を、印刷などで用いられているシアン・マゼンダ・イエローのCMY減算混色で表現された色（スペクトル）へと変換します。その逆に、CMYからRGBへの変換を行うのが、Spectrum Color Conversion::CMYtoRGB です。各色に対する入力値は、RGBtoCMY・CMYtoRGBのいずれの場合も、0から255までの値を入れるようになっています。なお、CMYtoRGB の際のD65という欄には、255という数値が入っていますが、これは減算混色時にインクを照らす照明光の明るさです。この数値を変える必要は特にありませんが、もしも、この照明光D65の強度を変えたりしてみれば、その強度に応じて明るくなったり・暗くなったりすることは確認できると思います。

　CMY<=>RGB の色変換の際に用いている基準は、「スペクトル強度の差の自乗和が最小になること」です。つまり、人の視覚特性などに特化した色変換ではなく、単純に分光強度の形状が近くなるような色変換を行っています。また、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルは非常に大雑把な値を使っています。特に、シアン・マゼンダ・イエローに関しては、印刷で用いられているインクとは異なり、比較的理想に近い吸収スペクトルの場合を示しています。もしも、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルを眺めてみたい場合には、RGBtoCMYやCMYtoRGBの入力値として、単色だけを255にして、それ以外の色を0にしてみて下さい。たとえばシアンだけがある場合の単色スペクトルを眺めたければ、シアン=255, マゼンダ=0、イエロー=0にする、という具合です。すると、その色だけを使った時のスペクトルを見ることができるわけです。ただし、減産混色の場合に表示されるのは、いわゆる吸収スペクトルではなく、インクに吸収されなかったスペクトルということになります。また、CMYが示している量には対数変換がかけられています。

　RGBtoCMYとCMYtoRGBは、相互に入力スペクトルと再現されたスペクトルを比較することもできますから、RGBとCMYの間で相互に色変換を繰り返しながらスペクトルの変化を眺めてみるのも面白いかもしれません。

　なお、このSpectrum Color Conversion は、離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージをWolfram Technology 社のMathematica上で作成し、webMathematica エンジンを用いることで、web アプリケーションとして動作しています。

• 分光画像処理入門
• 応用Mathematica

■「無名関数」と「吾輩は猫である」　

　夏目漱石の「吾輩は猫である」は、雑誌「ホトトギス」に1905年1月に発表された。最初は、冒頭の章だけで完結する短い読み切り小説だった。

　吾輩は猫である。名前はまだ無い。　…吾輩がこの家へ住み込んだ当時は、主人以外のものにははなはだ不人望であった。どこへ行っても跳ね付けられて相手にしてくれ手がなかった。いかに珍重されなかったかは、今日に至るまで名前さえつけてくれないのでもわかる。

　「吾輩は猫である」を連想したのは、Mathematicaの「純関数」の勉強のための練習題材を書いていたときだ。Mathematica の入門・中級の講習会に参加すると、この純関数とやらが登場した途端に、講師が話す内容を見失ってしまうことが多い。講師の筋道が見えなくなってしまう理由は、純関数の必要性・存在価値といったものが今ひとつわからないままに、純関数がいきなり登場してくるからである。もちろん、「（数値でなく）関数を引数として与える」ということに慣れていない生徒が多いこともあって、いつも、純関数が登場した瞬間に、何かその場が失速したような感覚を受ける。

　話の流れ・必然性がなくても、文法をただ暗記することができる人であれば、おそらく何の問題もないのだと思う。あるいは、他のプログラミング言語をよく知っていて、文法の必然性が自然と理解できる人たちであったなら、これもまた問題は起きないのだろうと思う。しかし、私も含めて、入門・中級の講習会に来ているような、そうでない多くの人たちの場合は、純関数が登場した途端に、話についていけなくなることが多いように感じるのである。

　Mathematica における純関数 "Pure Function" というのは名前(シンボル)を持たない関数で、ほかの関数への引数などとして、関数の内容を書いた一瞬だけ使われるものだ。もう少し違う呼び方をしてしまえば、つまりそれは「無名関数」だ。「無名」というところが重要で、名前がないから、使ったら最後もう二度と呼ぶ・使うことはできない、ということである。つまりは、「使い捨ての関数」だ。この「関数を使い捨てる」というところで、どうしても引っかかってしまう。値を入力するのであれば、あまり考えることなどせずに、数字キーを2・3回押せばすむ。だから、値に名前（シンボル）と付けずに、使い捨てにすることには慣れている。けれど、関数を書く場合には、（ハッカーでない私たちは）頭も多少使わざるをえない。すると、せっかく考えて・苦労して書いたのだから、名前をつけて、あとで呼んでまた使うことができるようにしたい、などと思ってしまうのである。使い捨ての「無名」ということと、苦労をともなう「関数」ということを、なかなか重ね合わせることができないのである。

　そこで、自分なりの「純関数の存在価値・意義」を作ることで、その存在意義を納得したくて、純関数を使った例題を作ってみた。実は、それが前回の Spectrum Color Conversion を動かしているベース部分、「離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージ」である。これは、無名関数（純関数）を使うための例題である。このパッケージを使うと、スペクトルを描くのに、

plotSpector[ (128 red[#] + 255 blue[#])& ];

(128 red[#] + 255 blue[#])&

rgb=fitSpector[(D65[#]-128 cyan[#])&,red,green,blue]

　こんな例題を作ることで、無名関数アレルギーが低減した、と言いたいところなのだけれど、関数を使い捨てることには、やはりまだ慣れることができそうにない。関数を引数として渡すことは自然に感じられるようになっても、無名関数に名前をつけて、再度その関数を呼んでみたい気持ちはなかなか止められそうにない。名前をつけるより、その関数の中身をそのまま書いた方がわかりやすいとわかっていても、単純な名前をつけてしまいたくなる欲望はなかなか止められそうにない。

　その理由を考えてみると、やはり、苦労をともなう「関数」を使い捨ての「無名」にしてしまう、ということに一因がある。そして、もう一つ、名前をつけることで、単純化して安心してしまいたくなる、ということがあるように思う。ほんの何文字かの関数であっても、その内容を自分の頭で考えるよりは、なにがしかの単純な言葉で表現された関数名を聞いて納得したくなることがあるように思う。

　「吾輩は猫である」の第一章の最後、つまり、当初の読み切り短編小説「吾輩は猫である」はこのように結ばれる。

　吾輩は御馳走も食わないから別段 肥りもしないが、まずまず健康でびっこにもならずにその日その日を暮している。鼠は決して取らない。おさんは未だに嫌いである。名前はまだつけてくれないが、欲をいっても際限がないから生涯この教師の家で無名の猫で終るつもりだ。

■静的・動的/連続・離散化、経済循環モデルの実装は難しい…　

　まだまだ、中谷巌　「入門マクロ経済学」のページをめくりつつ、その中にあるマクロ経済循環の図をなぞりつつ、Simulinkモデルを作っています。作っているSimulinkのmdlファイルは、ここ（今日時点での最新版はmacromodel_basic_20090307.mdl）に逐次置いてます。

　ラフスケッチ的なモデルであったとしても、全体像を形作ろうとすると色々な勘違いや、まったく理解できていない点にたくさん気づかされます。「入門マクロ経済学」のイントロダクションに書かれている

　経済学の難しさは、細部についてかなりの理解に到達したとしても、全体像がつかめないと、なかなか論理の一貫した議論ができないという点にあります。

　教科書のページをめくりながら、Simulkinkでモデル実装しようとすると、まず読んでいる頁に書かれている事項が「静的（静学的）」なのか「動的（動学的）」なのか、ということが今ひとつわかりません。どうも静的・動的の区別がつかないと、モデル実装のしようがありません。

　さらに、動的な場合、連続的なものなのか離散化されたものなのか、という点についてもよくわからず悩みます。さらに、離散化されたものの場合には、その時間ステップについて、異なる時間ステップのものが混在していないか、どう切り分けるか…といった点について悩むわけです。また、何かの値を使うとき、その値をどういった微分・積分の階層で整理・実装するかなども、悩むところです。

　何だか「機械・制御システム」を作る時に感じるだろう課題が、この経済循環モデル実装作業には、てんこ盛りに詰まっているように思います。入っていないのは浮動小数点から固定小数点や整数処理に変える際の精度保証・オーバーフロー対策の苦労くらいではないか、と思うくらいです。逆に言えば、その難しさが魅力的だということも言えるかもしれません。

　Simulinkで今日作ってみたSinmulinkモデルが、下図になります。各市場部分の内部は(mdlファイルを眺めればわかるように)比較的単純な分配サブシステムになっています。そして、オレンジ色で囲んだ部分を見るとわかるように、これは計算時間ステップがほぼ1週間(Time=0.25)という動的離散化モデルで実装されています。そして、「Time=0～11(単位は月)=1年間」の計算終了時に、その1年間の国民総生産(GNP)などが計算される、というイメージで作ってみました。

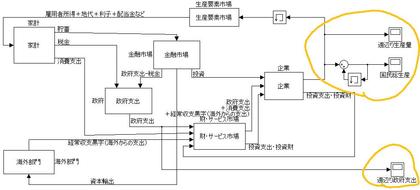
　前回作ったモデルとサブシステム配置はよく似ていますが、信号線を流れている値は一階層”微分”されたもの、が流れているという具合にした「つもり」です。あくまで、「つもり」なので、間違っているところも多々ありそうです。

　それにしても、本当に「一部を説明した文章・式」を納得することはできても、そういった一部が組み合わさった全体の実装は、とても難しいということをつづく感じさせられます。

　なぜか、以前書いた「長い文章を書くと言うこと」を思い出したのです。

　一言ふと漏らすコメントは非常に的確なものなのが普通です。だって、そのクローズアップされた狭い景色の中では特に「歪み」も「矛盾」もないのが普通ですから。だから、短い言葉・文章というのは、見事なまでに「その狭い世界」を写し取っているはずだと思います。
　ところが、もう少し広い世界を写し取ろうとすると、もう少し長い文章を使って大きなものを書こうとすると、途端に色んな「食い違い」が見えてきます。

■あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる　

　あみだくじを作ったとき、「アタリ」がどのような分布になるかは、大雑把には、拡散方程式で解くことができます。もし、あみだくじに横線があれば、右へ行ったり・左に行ったり、酔った人がさまよい歩く酔歩（ランダムウォーク）のように「アタリ」を選ぶことができる場所が、推移するわけです。

　たとえば、拡散方程式を横軸を縦線感覚で離散化し、縦軸は…これまた適当に離散化し、縦方向単位長さ移動するときに、どれだけ左右への移動が生じるか（＝横線が縦線に対して、どの程度の頻度で存在するか）を考えてやり、そしてその離散化された拡散方程式を解いてやれば「あみだくじ」のアタリ分布を計算することができます。

　左端と右端の「境界条件」では、そこで「折り返されたような」動きをするわけですから、ノイマン条件を適用してやればよいことになります。また、時間ステップは、いつものように「循環参照による手動再計算」を用いて実現してやれば良い、ということになります。

　というわけで、エクセルでプロトタイピングして、作ってみたのが下の計算シートです（作成したエクセルシートはここに置いておきます）。たとえば、下のグラフは、アタリが左から３番目縦下部にあった場合に、一体、どの縦線を選ぶの良いかを示す確率分布になっています。今のこの状態なら、左から１番目、２番目、３番目が大体同じアタリ確率になっていて、もう少し細かく眺めてみると、左から２番目を選ぶのが一番アタリをひく可能性が高い、ということがわかります。

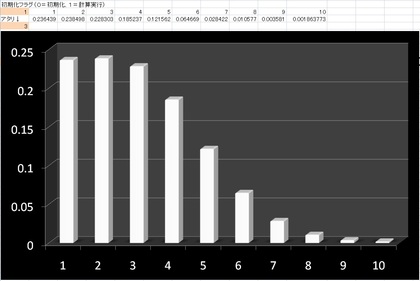
　上の例の場合には、一番アタリをひく可能性が高い線が、アタリのある真上より少し端側に寄りました。この「アタリをひく確率が高い線が端に寄る」傾向は、横線が多いほど激しくなります。…とはいえ、あみだくじを作る時のことを考えると、実際にはあまり横線の数が多くないように、つまり、手抜きあみだくじが多いように思います。

　そんな時は、手抜きあみだくじをするときは、アタリの真上近くを選び、そうでない場合にはアタリに近い端っこを選ぶ、というのが、あみだくじ方程式から導き出されるおトク知識と言えるのかもしれませんね。