1998-11-18[n年前へ]
■スクリーンセーバー用の画像ファイルを作ろう。 
Canon in HongKong 1998
以前、作成した「FilmStrip」用の「画像ファイル集」を作った。テーマは- Canon in Hongkong 1998 - である。何故、Canonかというと深い意味はない。
ダウンロード 「FilmStrip」用の「画像ファイル集」- Canon in Hongkong 1998 - (Copyright Jun Hirabayashi)
上からダウンロードしたファイルを解凍し、できた"bmp"ディレクトリを"C:\image"ディレクトリの下に置く。つまり、"C:\image\bmp"という形になる。そうすると、「FilmStrip」から使えるようになる。今回のテーマを使うと、実行中の画面は下の図のようになる。
 |
このように、テーマを統一した画像ファイル集を使うのが、「FilmStrip」の作者としてのお勧めである。今回の画像の共通点と言えば、
- Canon
- 街
- 原色
今回のテーマの色合いは35mmリバーサルであれば、エクタクロームかベルビアといった所だろう。FinePix700のようなフィルム会社が出しているデジタルカメラの色特性(色再現性ではない)には非常に興味がある。コピー機メーカーと(オリジナルとしての)フィルムメーカーが出すデジタルカメラの色特性はもしかしたら違う傾向にあるかもしれない。コダックの出すフィルムが黄色(会社のイメージカラー)を強調し、富士写真フィルムのフィルムが緑(会社のイメージカラー)を強調していた、というのは本当かどうかはしらないが有名な話だ。そのような意図的な色特性があれば、それは個性として面白い。しかし、コピー機メーカーにはそのようなオリジナリティな発想はないかもしれない。いつか、それについても考えてみたい。
1999-06-10[n年前へ]
■コピー機と微分演算子 
電子写真プロセスを分数階微分で解いてみよう
前回、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
の中で、電子写真プロセスは「画像のエッジ部分が黒くなり、そうでないソリッド部分は画像が飛びやすい... 画像のエッジ部分、すなわち、電位変化が大きく、電界強度の高い部分に対してトナーが現像されやすい... 」という文章がある。この脈絡は何か見覚えがないだろうか?そう、
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の中の、「人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。」という文脈と似ている。また、「ゼロックス...」の回での(昔の)電子写真の特徴、
- エッジ強調される。
- 細かいところはボケてしまう。
参考までに、以前の話のときに用いた画像を示しておく。
まずは、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
における(昔の)モノクロコピーを模したものである。
 |  |
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の際に解析した元画像と0.75階画像である。ただし、この解析は2次元解析ではなく、1次元における計算を回転させて、中心対称な画像を作成している。その理由は前回述べたので今回は述べない。
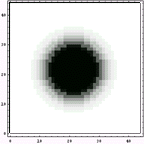 | 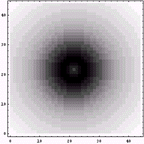 |
それでは、解析を始める。まずは、Photoshop5による「(昔の)コピー機シミュレーション」である
 |  |
次が、分数階微分画像だ。今回もMathematicaを用いて計算している。検算が終了したら、Notebookも公開予定だ(実は検算が終了していないのだ...)。
 | 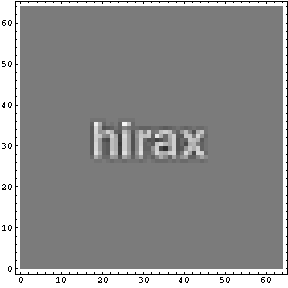 |
胸を張って「似ている」と断言するつもりはないが、少しは似ているのではないだろうか。別に似るまでがんばっても良いのだが、この分野の話はあまりやりすぎるわけにはいかないのである。ということで、強引ではあるが、今回の話の結論は「アナログコピーはオリジナルコピーの0.75階微分だ」というところで終わらせてもらう。
今回は、コピー機によるコピーを微分演算子と結びつけてみたわけだが、複数回のコピーに適用してみると面白いだろう。例えば、孫コピーは0.75+0.75階微分=1.5階微分であるとかだ。
また、同じ現像プロセスといっても色々あるわけであるから、各現像方式により微分演算子の階は異なるのが適当だろう。例えば、この機械は0.8階微分(つまりほとんどエッジ現像)であるが、こちらの機種は0.05階微分(極めて元画像に近い)で再現性に優れる、などという論議もできるかもしれない。
ところで、某所で今回の話と似て非なる話がCoffeeBreakとして公開されている。しかし、そちらは一般公開されていない。というわけで、今回は分数階微分の第3話ではなく、第4話ということになる。STARWARS風に言えば、Episode4だ。STAR WARSのようなSF映画もそうであるが、こういった話は生物(なまもの)である。ずっと置いておくと腐ってしまう。「腐ってこそ美味い食べ物もある」、という反論も聞こえてきそうだが、そういったものは少数の例外である。味オンチの料理人の作ったものではあるが、どうか賞味期間内に味わって頂きたい。