hirax.net::Keywords::「最小化問題」のブログ

■hodrick prescott excel add-in　

hodrick prescott excel add-in

　The Hodrick Prescott Filter Add-In was written by Kurt Annen. This program is freeware.

■Hodrick-Prescott フィルタのナゾ!?　

　経済オンチ解消のため、まずは景気動向を眺めてみようとふと思い、景気データを解析する手法について調べてみました。その作業をする中で、景気データから周期成分を取り除き、トレンド成分を導く手法の"Hodrick-Prescott filter"が気になり、頭から離れなくなりました。

　" Hodrick-Prescott filter"というのは、離散的な時系列データy(t)が与えられたとき、そのトレンド成分をτ(t)とすると、下記のような評価関数を最小化するようにτ(t)を定める、というものです。ちなみに、y(t)、および、τ(t)は、景気データを対数(log)値で示したものになります。

　この式を眺めれば、第二項は二階微分を中心差分でとり、その結果をデータ全域にわたり積分したものだということがすぐわかります。つまり、（景気データを対数軸で示したときの）直線からのズレ・ジグザグ度合いです。その直線からのズレ度合いに定数λを掛けたものです。ちなみに、このλは離散データが三か月ごとのデータであれば、（多くの場合）1600が使われます。もしも、サンプリング間隔が密になれば、二階微分の結果が小さくなるので、それを補うように大きな値が用いられます。また、サンプリング間隔が疎であれば、二階微分の結果は大きくなるということで、ラムダには小さな値が用いられます。たとえば、サンプリング間隔が１年なら、（多くの場合…は以下省略します）λは100が用いられますし、月ごとのデータであれば、14400が用いられますが、これは「二階微分値に対し自乗をとっている」ことを考えれば（その自乗分に比例定数λを合わせようと思うなら）、なるほど、と思えるはずです。

　また、第一項目は、トレンド成分と実データのズレ＝取り除きたい周期成分、をデータ全域にわたり積分したものです。ということは、このHodrick-Prescott フィルタは、「実データにトレンド成分がなるべく沿うようにした上で（第一項）、トレンド成分がなるべく対数軸上で直線になるようにする（第二項）」というものであることがわかります。そして、その第一項目と第二項目に対するバランス（評価関数の重み）が、第二項に掛けられてるλで与えられる、というわけです。λが大きければ、「実データから”周期成分”を大きく取り除く＝対数軸上で直線になるようにする」ことになりますし、ラムダが小さければ、「対数軸上での直線からのズレが大きくなってもいいから、実データに沿う＝”周期成分”をあまり取り除かない」ということになります。

　解説論文を読んだ印象は、この式のλは「米国景気データをもとにした合わせ込み（上手くつじつまがあうようにλを設定する）」で求められた結果であり、また、「対数軸上で景気動向は直線になる」という前提（背景）のもとに作られている、という具合です。（参考：「トレンドとサイクルの分解」の「実際には単位根の問題や成長率を問題にすべき点から、対数階差を原系列データにほど こしてから分析すべき」という辺り）

　このHodrick-Prescott フィルタが頭から離れなくなったのは、「Hodrick-Prescottフィルターをかける前の変数変換」という、専門の先生による記事を読んだからです。この記事では、Hodrick-Prescottフィルタは「そのままの値」にかけるのか、「対数変換した値」にかけるのか、それは「対数変換した値」が一般的だろう、と説明された上で、

　そのままの値にH-Pフィルターをかけた結果と対数変換した値にH-Pフィルターをかけた結果は基本な形状は変わらないはずですが、スケールが変わってしまうので注意が必要ではないかと思います。

　疑問を何とか形にしてみると、それはHodrick-Prescottフィルタの評価関数が「対数軸上で景気動向は直線になる」という考えのもとに作られているの（ように見える）に対し（しかも、評価関数の第二項目は単に景気のトレンドを（与えられた軸で）直線にしようとする働きしか持たないにも関わらず）、線形値に対してHodrick-Prescottフィルタを掛けた場合、「対数軸上で現した場合に景気動向が直線になる」ようなトレンド成分が得られるのだろうか？本当に「基本な形状は変わらない」のだろうか？という疑問です。この評価関数を最小化しようとした場合に、対数軸でも線形軸でも「基本な形状は変わらない」のはどうしてだろう？という疑問です。

　きっと、式を追いかけてみれば、あるいは、いくつかの例を解いてみれば、この疑問は解消する（理解できる）はず…と思えます。というわけで、とりあえず、この「Hodrick-Prescott フィルタのナゾ!?を解く（きちんと理解する）」ことを、メモ帳のTo Doリストに書き入れておこうと思います。

■実は体育会系な 「京都市鴨川源流」を廻る「理系風デート」　

　今はカリーニングラードと呼ばれ、かつてはケーニヒスベルクという名前だったバルト海沿いにあるロシアの街を舞台にして、「流れる川により区切られた土地を、一筆書き状にすべて渡り、スタート地点に戻ってくることができるか？」という「謎かけ」が、「ケーニヒスベルクの橋渡りの問題」です。

　ケーニヒスベルクでなくとも、日常生活をする中で眺める街の景色の中にも、「ケーニヒスベルクの橋渡りの問題」は結構顔を出しているものです。たとえば、それは川崎の東京湾寄りのTOKIOのDASH海岸がある辺りに行けば、「ケーニヒスベルクの橋渡り問題」な案内看板を見かけることができます（街で見かけた「ケーニヒスベルクの橋渡り問題」）。そして、京都市街東部を流れる鴨川辺りにも、そんな「ケーニヒスベルクの橋渡り問題」があって、そこを巡る「理系風デート」が有名？であったりします（「京都市鴨川源流」を廻る「理系風デート」）。

　実際に鴨川辺りに行くと、「この橋渡り問題を解くべし」と、まさに「ケーニヒスベルクの橋渡り問題」な地図・看板がたくさん掲げられています。面白いことに、それぞれの地図ごとに川に渡された橋の数が異なっていて、つまり、地図ごとに「答え」が違うことに気づかされます。ある地図では、一筆書きが可能だけれども、ある地図では一筆書きをすることは不可能だということがわかったりするのです。…それを逆に言えば、地図ごとに答が違うからこそ、「ケーニヒスベルクの橋渡り問題」な地図を見つけるたびに、新しい問題（地図）を解く楽しみが生まれる、ということなのです。

　「一筆書きできる地図」を見つけ出し、一筆書きをしつつ川縁（かわべり）を回ってみても楽しいし、あるいは、川端（かわばた）にあるたくさんの「ケーニヒスベルクの橋渡り問題」な地図を眺め、それら「ケーニヒスベルクの橋渡り問題集」を解いて回るのも面白いものです。

　ところで、実際に「京都市鴨川源流」を廻る「理系風デート」をしてみると、結構長い距離を回らなければいけないことに気づきます。徒歩で歩き回るのはもちろん大変ですし、自転車で走り回るにしても、…やはり結構な時間ペダルを漕がなければなりません。また京都市街は南に比べて北の方が標高が高い、当たり前ですが、鴨川下流よりは上流の方が標高が高いわけですから、（目に見えないほどの斜度とはいえ）北上する時には坂を登る体力が必要です。

　たとえば上に貼り付けた地図のように、橋と橋の間の距離や、橋と橋の間の標高差が書かれている「ケーニヒスベルクの橋渡り問題」も見かけます。こんな問題（地図）を見かけたならば、「一筆書きをすることができるか」という問題だけでなく、「移動に必要な体力を最小化するにはどうしたら良いか」という（いわゆる）制約条件付き最小化問題を解いてみるのも興味深いかもしれません。…そして、その最小化問題を解いたなら、地図から解き明かした答えを確かめるべく、ひたすら鴨川の川縁（かわべり）を汗をかきつつ走り回るのです。

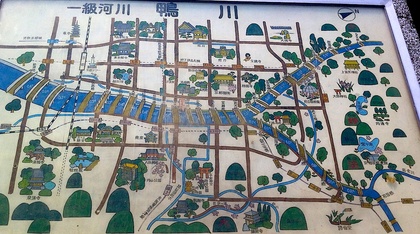
　「京都市鴨川源流」を廻る「理系風デート」は、実はとても体力を使う、実はかなり体育会系なデートです。少しだけ頭を使って考えたことを、体力と根性で確かめる、そんな楽しい「ケーニヒスベルクの橋渡り問題」なのです。