hirax.net::Keywords::「表計算プログラムでシミュレーション」のブログ

■エクセルでシミュレーション Vol.1 [静電界準備 編]　

　「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは（私たちのような勉強世界からの REST OF US にとっては）とても素晴らしいと思います。

　ところで、現在では”表計算プログラム＝マイクロソフトのエクセル(Microsoft Excel)”だと考える人も多いことでしょう。だから、上に書いたことを言い換えれば、「エクセルでシミュレーションをする」のは、とても楽しい勉強になるということになります。

　自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備（事前確認）」をしてみました。

　まず、静電場を記述するポワソン方程式をテーラ級数展開することで離散化し、差分方程式に変えてみます。２次元世界を離散化するということは、エクセルの表がそうであるように「世界（画面）をセルで分割する」ということです。

　この離散化された後の差分方程式は、つまり「セル間の計算（関係）式」ですから、「２次元静電場を記述するポワソン方程式を、（エクセルの）セル間の計算式で解く」ことができることになります。

　上で（x,y座標空間での）差分方程式にしたものを、さらにエクセル（表計算ソフトウェア）で解くときのやり方を図解したものが下の図です。「ある点の電位（φ）は上下左右の電位の平均にその点の(係数がかかった)空間電荷を加えたもの」になっているわけです。

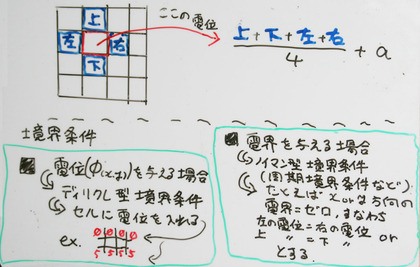
　また、2種類の境界条件（電位を指定するディリクレ条件/電界を指定するノイマン条件）をどのようにエクセル上で処理するか、というのが下の部分になります。

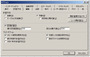
　こういったセルの値が「（そのセル自身を含む）セル間の関係式」で表わされるような計算式を解くためには、エクセルの設定で「反復計算を行う」という設定を有効にしておく必要があります。エクセルのバージョンによってその設定メニュー場所は違いますが、たとえば、下の画面はExcel 2003の設定ダイアログの例です。

　以上で、「静電界を記述するポワソン方程式をエクセルで計算するための前準備（事前確認）」が終わりましたから、次は実際に「身近な静電界」をエクセルでシミュレーション計算してみたいと思います。

■エクセルでシミュレーション Vol.2 [静電界計算の動画 編]　

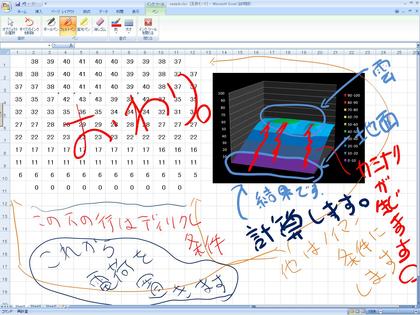
　エクセルでシミュレーション Vol.1 [静電界準備 編]で、（ポワソン方程式で表わされる）静電場の計算をエクセルでする準備作業ができたので、実際にエクセルで静電界計算をしてみました。どのような状態を計算してみたかというと、「夏の空に帯電した雲が生じた時の、地面から空へ向かう空間の断面の電場」の状態です。地面をグラウンド＝０Vとして、空に電荷を帯びた雲が浮かんでいる状態を計算してみました。エクセルを使って、その計算シミュレーションをゼロから作り上げ、結果を描き終わるまでの8分弱の動画が下のものになります。また、mpeg形式の動画ファイル(65MB)もここに置いておきます。

　夏の雷雲は負の電荷を帯びていることが多い、といいます。上のシミュレーション条件では、（動画を見ればわかるように、式後半に正電荷を入れましたから）雲の部分に正電荷を帯びさせましたが、そこは正負をひっくり返せば良いだけです。夏の日、暑い午後、都会や田舎の空に雷雲が見えてきたら、そのときの電場シミュレーションを（突然の落雷による停電に気をつけながら）PCのエクセル上でしてみるのも、気分転換になるかもしれません。

■エクセルでシミュレーション Vol.3 [夏の午後の雷雲の下 編]　

　エクセルでシミュレーション Vol.2 [静電界計算の動画 編]で、「地面と空に浮かぶ雷雲」を含む世界の静電場計算を行うエクセルシートを作ってみました（あくまで2次元ですが）。そこで、前回とは少しだけ違う”いかにも夏らしい”２つの例を計算してみました。

　まず最初の計算は、地面の上に人が立っている状態です。空を見上げると、頭の上には雷雲が広がっていて、いかにも不安を感じている状態です。

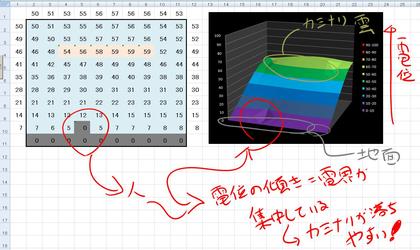
　計算結果を見ればわかるように、人体部分に電界が集中していて、すぐにもカミナリに打たれてしまいそうなことがわかります。

　これは怖すぎる……というわけで、人の少し横に避雷針を立ててみたのが、次の例になります。高さのスケールが少し変に見えますが、そこら辺は適当に無視しておいて下さい。とにかく、人の少し横に避雷針を立ててみたわけです。

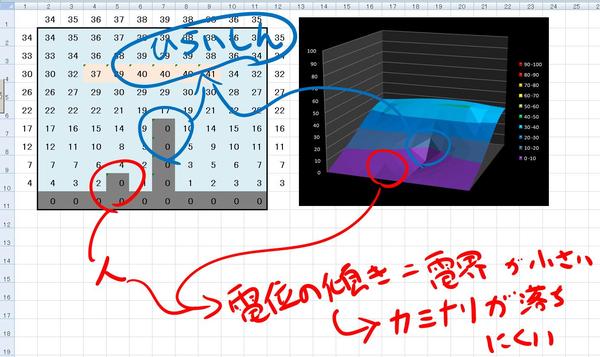
　すると、今度は避雷針の先には強い電界が集中していますが、人がいる部分ではほとんど電位変化がないことがわかります。ということは、カミナリに打たれる心配もなく（といっても近くに落ちるカミナリはやはり怖いですけれど）安心していられる……ということがわかるわけです。

　そういえば、もう夏ですね。日差しを強く感じる暑い午後に空を見上げると、いつも白い積乱雲が見えます。暑い夏を楽しみつつも、夏バテにはお気をつけください。

■エクセルでシミュレーション Vol.4 [定常理想流体準備 編]　

　夏の午後の空に浮かぶ雷雲を見ながら、昨日は静電界シミュレーションをマイクロソフト・エクセルで手軽にしてみまたわけです。暑い夏空をシミュレーションしてみたので、今度は、冷えた湧水が地下で流れているを眺めてみたくなりました。そんなシミュレーション計算をするために、理想流体の「定常的な流れ場」を表計算ソフトで解くための前準備を、今日はしてみました。

　というわけで、そのためのラクガキが下の画像になります。

　ここまでくると、もう「エクセルでシミュレーション Vol.1 [静電界準備 編]」と同じです。ポワソン方程式とラプラス方程式は、端的に言ってしまえばほとんど同じなので、後は「２次元の（ポテンシャル）流れ場を記述するラプラス方程式を、（エクセルの）セル間の計算式で解く」ことができることになります。

■エクセルでシミュレーション Vol.5 [冷たく美味しい湧水 編]　

　暑い夏空の下、私たちが立つ地面の遥か奥底で流れる地下水が、長い時間をかけ湧水地にまで流れてくるようすを眺めてみたくなりました。そこで、そんなシミュレーション計算をしようと エクセルでシミュレーション Vol.4 [定常理想流体準備 編]で計算の準備をしてみました。

　というわけで、準備したワークシートが下の画像です。左上に山腹の高原湖があって、右下には海辺近くにある湧水群がある、という具合です。右上半分は青空で、一番下の列は固い岩盤が水を遮っている、というのがこのエクセルのセルで描かれたモザイク画です。

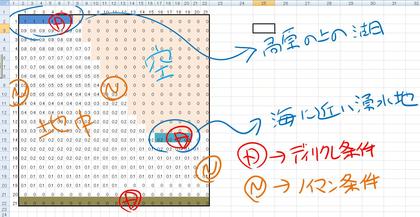
　上のような状態で、定常な理想流体のポテンシャル流れを計算してみた結果が、下の図になります。左上の湖水が地中に沁みわたり、ゆっくりと時間をかけて冷えて漉されて美味しい水となって、湧水地に辿り着くまでの姿が見えてくるような気がします。

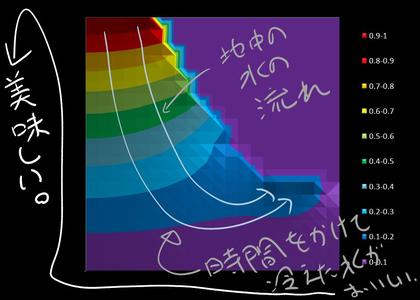
　エクセルのグラフからは見えてこないかもしれませんが、富士の近くで眺める湧水は本当に澄んでいます。空の色を少し映して、ほんのりと水底を青緑色に染め、その上の水面に夏の青空と白雲を重ねた、そんな景色を見せています。