2009-12-29[n年前へ]
■「カルマンフィルタ」と「エクセルで解く2次元非定常熱伝導問題」 
正月に、（自分用の）汎用「カルマンフィルタ」ライブラリをRubyとCとExcelで書いてみることにした。たとえば、さまざまなデータ、たとえば、信頼性が低く、誤差の大きなセンサデータや、安定性に欠ける実験データから、現実に近い状態量を推定するツールを作ってみることにした。そして、何か（解析式による）モデル計算や各種シミュレーション計算と比較をしてみたり、それらの計算改善へのフィードバック例を作ってみよう、と考えた。
そこで、扱う題材を考えつつ、実際に上記のようなことを行っている例を探してみた。すると、たとえば、
といったものがある。これらの記事が（下に張り付けた動画でその一端がわかると思うが）実にわかりやすく・面白くて楽しく・役に立ちそうに見える。何というか、つまるところ、魅力を持つに必要な三拍子がすべて備わっている。
先日、「２次元非定常熱伝導問題を解く」エクセル・シート、しかも、そのシートに、センサ機能／フィードバック機能なども付けてみた。そんな素材・材料が揃ってきたこともあるので、まずは、PID制御で（疑似三次元空間における）温度制御を行う例をいくつか作り、その後は、上記記事を参考にしつつ「（誤差を付加した）センサ→カルマンフィルタ→制御量最適化」という例でも作ってみることにしよう。
2014-05-27[n年前へ]
■エクセルでラプラス方程式を解いて「血管がある皮膚周りの光強度分布」を計算してみよう!?
赤い血が流れているはずの血管が青く見える理由で行った計算を大雑把に解けば、たとえば完全拡散体として扱うことができます。それはすなわち、任意の微小領域が周囲に発する光強度は周囲（の微小部分が発する光強度）の平均値になるということで、つまりはラプラス方程式で表される解になります。
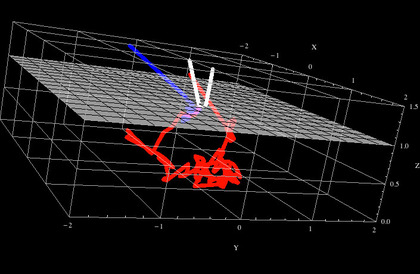
…というわけで、ラプラス方程式を離散化して、お手軽なエクセルで「皮膚内部に血管がある時の、その周辺の皮膚内部・表面での光強度分布を（たとえば青色波長で）可視化してみたのが下図になります。エクセルの各セルは離散化された空間上の各領域を示していて、そこに示されている色と値が光強度を示しています。
画面真ん中辺りに（画面＝シート鉛直方向に）血管が流れていて、画面＝シート上側にあたるのが皮膚表面です（画面下側が皮膚最奥部です）。
さらに青色・赤色波長の「（光が散乱して方向を変えるまでの）平均自由行程」を踏まえて、表面での光強度分布の違いを描いてみると、限りなく大雑把な近似に基づいた計算をすると、下図のような感じです（縦軸はその波長における周辺近傍の平均強度を基準にした相対値です） 。
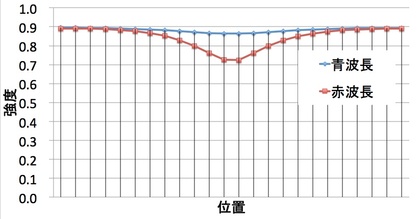
血管が下部にある部分を眺めると、青色波長では、その周囲の部分とさほど変わらない光を発しています。けれど、そこを赤色波長で眺めれば（表皮近くの毛細血管ではなく）皮膚下部に流れる血液に光が吸収されて、光強度が（近傍周囲より）減少していることがわかるかと思います。…だから、赤い血が流れているはずの血管が（周囲に対して相対的に）青く見える、というわけです。
」など。