hirax.net::Keywords::「パラドクス」のブログ

■アンディ・ウォーホルと"inter view"　

　"double meaning"で、その二つの"meaning"が相反すること、にいつも見とれる。二つの重なる言葉、けれど、それらがまるで反対のことを意味する言葉が好きだ。なぜなら、それが現実だから、だと思っている。もしも、片面しか見せないものがあるとしたら、（このフレーズは何度も書いているが）映画のセットのように薄っぺらいものでしかない、と思っている。"inside out"なんていう言葉が好きな理由は、そんな気持ちからだ。

　アンディ・ウォーホル・ミュージアムで、ウォーホルが創刊した「インタビュー(interview)」誌が壁の一面に並んでいた。多くの観客は、表紙に描かれたインタビューイの表情を眺め、それが誰かを確かめる。そして、傍らにある本棚からそのインタビューイが語った言葉を眺めている。

　その雑誌「interview」というタイトル・ロゴは、デザインのせいか、どれもすべて"inter View"という風に見えた。「内面を覗いたもの」というタイトルの雑誌と、アンディ・ウォーホルの「僕を知りたければ作品の表面だけを見ればいい。裏側には何もない」という言葉、そのまるで反対の言葉、"double meaning"な言葉がとてもいい。

　「表面だけを見ればいい。裏側には何もない」という言葉は、その「裏側の実在・裏側に惹かれる心」があってこそ、の言葉だと思う。「表面だけ」で「後ろに何もなかったとしたら」、それは後ろに倒れてしまう。・・・だから、と書き続けるには論理的に飛躍があるけれど、「表面だけを見ればいい。裏側には何もない」という言葉が意味を持つためには「裏側の実在・裏側に惹かれる心」という方向性がなくてはならない。つまり、これは一種のパラドクスな言葉である。それが、実に的確だ、と思う。

■無限の資源である人間と有限の時間というパラドクス　

　J.P.ホーガンの「断絶への航海 "VOYAGE from YESTERYEAR"(ハヤカワ文庫SF) 」から。

　「人間の心は無限の資源だって言ったけど、でもそれは無駄使いしないとしての話だ。これ、面白いパラドックスだと思いませんか？」

■「無限」に足しあわされた「有限の世界」　

　「無限個の数字を足し合わせていった結果（和）が、意外なほどに小さな有限の数になる」ことを不思議だと感じない人は多いと思います。たとえば、A4サイズの紙を半分に折って、その半分をさらに折って、その半分をさらに折って・・・と、無限に折り続けても、その紙片の総和はたかだかA4サイズに過ぎません。「無限の個数を足し合わせても有限の大きさにしかならないこと」も別に不思議ではないし、「有限の大きさのものを切り分けて、無限の個数のものをつくることができる」のも、当たり前田のクラッカーだ、という感じ方です。

　そういう人であっても、その「内容」次第で、第一印象でその内容を「自然」と感じるか「不思議」と感じるかは違うのではないでしょうか。たとえば、「アキレスと亀」のパラドクスを不思議だと感じる人もいます。その一方で、「無限個の時間を足し合わせた結果は、無限になることもあれば、有限になることもある。そして、この例の場合には和は有限になる」と自然に思う人であれば、この「アキレスと亀」の話には、特に興味を持たずに終わるかもしれません。

　あるいは、「地点Aから地点Bへ移動するためには、まず地点Aと地点Bの中間地点Cに到達しなければならない。さらにCからBへ移動するためには、その中間地点を経なければならない。・・・ということを延々考えてみるならば、地点Aから地点Bまで移動するには無限の点を通過しなければならず、有限の時間で移動することは不可能である」という「内容」を、自然に納得し・あたまをひねってしまう人もいるでしょうし、その一方で、そのロジックを聞いて頭を左右に振る人も多そうです。

　もしかしたら、初項a0,公比rの無限等比級数(等比数列の和)は「初項/(1-公比)」なのだから…と、いつでも、どんな問題に対しても常に同じような感覚を持つ人もいるかもしれません。

　ところで、こんな問題ならどうでしょう。「手元にボールがあり、このボールは、衝突のたびに運動エネルギーの半分を失います。ためしに、手の高さ、1mの高さから、そのボールを落としてみることにします。すると、そのボールは地面に衝突し、運動エネルギーの半分を失い、50cmの高さまで到達したのちに、また地面にぶつかり（さらに運動エネルギーの半分を失い）・・・ということを考えるとき、そのボールは無限時間運動を続けるか、それとも、有限時間内に停止するか？」という問題です。

　先ほどの式で示される有限時間でボールの運動エネルギーは消えてなくなると即答する人もいそうですし、もしかしたら、ボールの運動エネルギーは無限時間後までゼロになるわけがない、だからいつまでもボールは動き続けるに決まっていると断言する人もいそうです。

　「無限」「有限」というものほど、感覚を裏切るものはないのかもしれません。私たちの世界はまさに「無限」だとも言えるかもしれませんし、それこそ「有限」だと感じることも多いかもしれません。無限の可能性もあることも真実ですし、それと同時に、その世界には有限の時間しかないことも、これまた事実です。

　「無限」のはずの「有限の世界」を目の前にして、あなたはどんなことを考えるでしょうか？「無限」と「有限」とパラドクスを読んで、あなたの連想することは一体どんなことでしょうか。

■続 （ブラジャー）カップサイズのパラドックスを解き明かせ! - ブラの幾何学 型紙 編　

　「アンダーバストとトップバストの差という長さで定まるカップサイズを基準にすると、おっぱいの重さ＝体積はその３乗になっていまうのではないか、つまりは、（カップサイズが大きくなるにしたがって）おっぱいの重さは信じられないほど重く算出されてしまうのではないか…というオッパイの（ディメンジョンに関する）パラドックス 」と解き明かすために（参考：（ブラジャー）カップサイズのパラドックスを解き明かせ!）、裁縫教室で、ブラジャーの「カップ」の作り方（ブラの型紙）を眺めてみました。もちろん、そのココロは「きっとブラジャーのカップが大きくなる度合いは、1/3乗の比例するような具合だろう」という想像と期待を込め、調べてみたのです。

　下の図は、アンダーバスト長違いにおける、カップサイズ（アンダーバスト長とトップバスト長の差 cm）とカップ径 cmの関係を示した結果です。なんと、このブラジャー型紙データは、アンダーバスト長とトップバスト長の差 cmとカップ径 cmは見事に１次の比例関係になっています。…つまり、カップサイズの３乗でおっぱいの体積・重さが増大してしまう、ということになります。

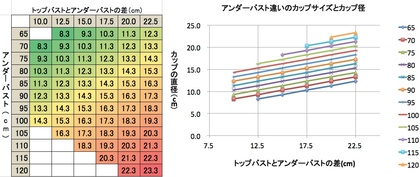
　一体全体、おっぱいの大きさ（体積）・重さは、カップサイズに比例するのか・しないのか…一体何乗に比例するのか・しないのか…オッパイの（ディメンジョンに関する）パラドックスは、一朝一夕で解ける問題ではなかったようです。

■「現実にはありえない」照明状態の「道路沿いのパラドクス」を現実にしてみよう！？　

　アニメーションの作画をする際に、絵の印象を良くするために「現実にはありえない」照明状態で描くという「道路沿いのパラドクス」テクニックの話を面白く読みました。この話を読みながら、ふと「そんな不可能立体を杉原厚吉先生風に現実に作り出してみるのも面白いかも」と考え、雑に適当に「現実にはありえない」照明状態の「道路沿いのパラドクス」を現実にしてみました。

　雑に３Dラクガキした程度なので出来はイマイチだったり、「そもそも現実にはありえない」感じが増幅しただけ…のような気もしますが、とりあえず「がんばりました」と日記には書いておくことにします。