hirax.net::Keywords::「定義式」のブログ

■「マンハッタン距離」と「続　理系風デート」　

　万城目学のエッセイ集「ザ・万歩計 」のこんな一節を読んだ。

　京都の生活には、自転車がよく似合う。

いわゆる京都市内、つまり、山あり谷ありではない市内を移動するには、確かに自転車が一番適している。周辺部以外には、曲がりくねった道はなくて、道はすべて真っ直ぐ東<->西か南<->北方向に走っている。だから、どこに向かうにもただ、目的の方向に進み・曲がればいいだけだ。

　出発地から目的地まで行くのにかかる時間を見積もる、つまり、出発地から目的地まで行く経路の距離を計算するのだって、とても簡単だ。上に書いたように、平安京の時代からある京都市内中央部は、碁盤の目状に道が配置されている。だから、経路の距離は「マンハッタン距離」で計算することができる。東京の街中なら、不定形の道に沿って線積分する必要があるだろうし、野原の真ん中なら…少しは単純だけれど「ユークリッド距離」を計算するために平方根（ルート）を計算してやらなければいけない。そんな計算は面倒だ。しかし、京都市内は違う。

「京都市内の距離空間はマンハッタン距離で計算できるのがいいね」
「目的地までの東西距離と南北距離を足すだけでいいから、計算が簡単でいいよね」
「どの平方根…じゃなかった、ルートでも距離は同じだしね」

といった、自転車に乗りながらの理系風会話が日常的にしやすい。もちろん、「マンハッタン」距離なんていう一見オシャレに響く言葉を使っているので、理系風デートで使えなくもないフレーズである。

　しかし、その後に、こういうウンチクを口にし始めてしまったりすると、しかもそれが「理系風デート」ならその時点で「終了」していまうことが多い。

　あれ？マンハッタン距離を考えたヘルマン・ミンコフスキーって、機動戦士ガンダムのミノフスキー粒子と関係あるのかな？

　これで会話が続いたら、単なるガンダムおたくである。まさに、「若さゆえの過ち」「ぼうやだからさ」状態である。

　…とにかく、京都の町には自転車が良く似合う。先の万城目学のエッセイ「都大路で立ちこいで」でも、最後の一文はこう終わる。

　自転車で京都を走ることが掛け値なしに楽しい、ってことだけは、本当なのだ。

　京都の町に行くのなら、自転車を借りて市内を散策するのが一番いいと思う。紅葉間近のこの季節、天気の良い日なら、乗りやすいマウンテンバイクでも借りて、体育会風に（できれば2,3日かけて）京都を一周してみるのもいいと思う。それがたとえ、1日だけでも、やはり自転車で京都を走ってみたならば、バスや列車で街を離散的に巡るよりも、ずっと素晴らしく連続的な京都の街を知り・同時に楽しめると思う。

　「理系」と「文系」と言った話より、「頭」と「体」とか、「情緒/心/感情」と「論理」といったことの方に、今は魅力と確かさを感じる。自転車で巡る京都の町の魅力はは、少なくとも「体」と「情緒/感情/心」といった辺りの中心部を貫くと思う。

■ルートを外して、色んなものを眺めてみたい　（初出：2005年09月15日）　

　昨年の春頃、青春18切符のポスターがJRの駅構内に張られていました。もちろん、今でも(青春18切符が販売される)そのシーズン毎のポスターが貼ってあるわけですけれど、特にその時のポスターが好きでした。正確に言えば、そのポスターに書いてあった

√a = 18

旅路(ルート)の中では、人はいつも18(age)である。

という「小さな数式とその解説」が大好きだったのです。単純な数式と洒落た遊び心に、旅をする時の気持ちがこもっているように感じ、不思議なくらい心を惹かれたのです。

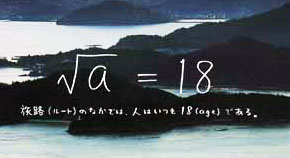
　しばらくしてから、そのポスターの数式とコピーに対する「この数式は、普通にa=324という答が出てしまいます」という指摘をどこかで読みました。その文章を読んで、「確かに、それは確かにそうだよなぁ」と思いつつも、私はふと屁理屈を書いてしまいました。…それは、こんなコジツケた屁理屈です。

　この数式で使われている"="は、いわゆる等号"= ="ではなくて、代入の"="かもしれません。つまり、この数式は「√a が 18 と等しい」ということを言わんとしているのではなく、「√aというものは全て18が代入される」という手順・代入式を意味しているということを意味しているのかもしれません。
　つまり、実はこの式は、方程式ではなく、"√"という関数(もしくは演算子)を定義する式なのではないでしょうか。
　…すると、この式は「"Root"をとると、どんなaを入力してみても、いつでも18になる」という意味になります。それを、さらに素直に言い換えるならば、「旅路(Route)の中では、人は誰でも18(Age)になる」というコピー文そのままに変身します。
　この式は、そういった「誰であっても18歳の頃に戻してしまう」ようなものが「旅路(Route)」なんだ、と高らかに定義・宣言する数式なのかもしれないと思いました。

　そして、さらにその数式から、さらに、「人のルート(Root=根底にあるもの)は、そんな18才の頃のようなものだよね」という強い意思を想像したのです。青春18切符のポスターに書かれた小さな式は、「旅は人を18歳の頃の気分にさせる。そして、それこそが - 人の根底- にあるものなのだ」と、そう伝えようとする言葉だと勝手に想像してみたのです。

　青春18切符の公式から"a=324"なんてなんだか当たり前の答を導いてしまうのは少しツマラナイ話です。もっと色んな答えを想像してみるのもきっと面白いと思います。

　そしてまた、例えば自分(や他人)のつまらない考えに沿った「決まり切った道（Route）」の上だけを走り続けるのも、なんだかつまらなく感じられることがあります。そんな時には、そんなルートを外して色んなものを眺めてみるのも、少し良いのかもしれません。　…あなたが「外したいと思ったことがあるルート」「外れたルート」「外したルート」は、どんなものでしょうか？