2009-05-13[n年前へ]
■「美的曲線」と「包茎手術」 
「美しい曲線」とはどんなものだろう?とふと思い、ネット検索してみると「美的曲線」というものが見つかった。
「美しさ」をアピールできることは,工業製品がマーケットで成功するために非常に重要です.例えば,自動車のボディの特徴線は,その車の美しさに対する印象を大きく左右します.本研究では,曲率対数分布図が直線で表される曲率変化の単調な平面曲線を美的曲線と呼びます.
和歌山大学の原田利宣先生が,「自然界や人工物におけるさまざまな美的曲線の多くは,曲率対数分布図が直線で近似できるということ」を指摘さまれました.原田先生が調べた美的曲線には,蝶の羽や自動車のボディのキーラインなどが含まれています.美的曲線の特別な場合として,曲率対数分布図における直線の傾きα=-1の場合にはクロソイド曲線,α=1の場合には対数螺旋となることが指摘されています.
なるほど、確かに「美的曲線」の例を眺めていると、その曲がり方の変化が気持ちの良い感覚にさせてくれるような気がしてくる。単調なカーブを描くのではなくて、曲率がほどよい速さで変化し、不思議な新鮮さを感じさせてくれる
・・・で、さらに「美的曲線」を調べていると、「美しい仕上がりの理由」というページを見つけた。「ひとつウエノ男になる上野クリニック」提供の「包茎治療を説明するページ」である。

上野クリニックでは「複合曲線作図法」という高度な技術を駆使した手術法を採用しています。これは、切除ラインが亀頭の傘の下に隠れるよう作図する美的曲線と、男性自身の裏スジの包皮小帯というひじょうに重要な部分を残す機能的曲線を組み合わせて作図する方法です。
患者様一人ひとりの皮の余り具合に合わせ、切除線を亀頭から3~5mmの箇所に設定します。傷跡がきれいに隠れ、手術したことが目立たない自然な仕上がりです。
上野クリニックの「美的曲線」が「曲率対数分布図が直線で表される曲率変化の単調な美的曲線」になっているかどうかはわからないが、「自動車のボディの特徴線」を語る言葉と、「男性自身の特徴線」を語る言葉が同じだったりすることが、何だか少し可笑しい。
2011-10-23[n年前へ]
■「トラック曲線=(半円+直線)×2」という運動会シーズンのナゾ!? 
 秋といえば運動会の季節です。この季節になると、いつも頭に浮かぶ「謎」があります。…それは「徒競走」をする校庭にある「トラック」の形に関する疑問です。
秋といえば運動会の季節です。この季節になると、いつも頭に浮かぶ「謎」があります。…それは「徒競走」をする校庭にある「トラック」の形に関する疑問です。
校庭のトラックは「両端の半円を直線で結んだ形」です。…はい、勘が鋭い人であれば、もう気づいただろうと思います。運動会シーズンにいつも考え込んでしまう謎というのは、なぜ
トラック曲線=(クロソイド曲線+円弧+直線)×2ではなくて、
トラック曲線=(半円+直線)×2なのだろう?ということなのです。
「トラック」の形状が「直線と半円」で形作られているとすると、直線コースから半円部分に突入した途端、急に、曲率がゼロからある程度大きな値に変わってしまいます。言うまでもなく、直線とは「曲率がゼロである」真っ直ぐな線であり、円とは曲率が一定の曲線であるからです。ということは、トラックを走るランナーたちは、体が進む方向を決める”ハンドル”をいきなり切らなければなりません(下図の黒線トラック)。
 しかし、高速道路のカーブと同じように、トラックのカーブにおいて直線と円弧部分をクロソイド曲線で繋いでおいたならば、最初から最後まで曲率が滑らかに変化していきます。クロソイド曲線というものが、曲率を連続的に変化させていく曲線なので、曲率ゼロの直線と任意の有限曲率を持つ円弧の間を、クロソイド曲線は滑らかに繋ぐことができるわけです。
ということは、トラックを「(クロソイド曲線+円弧+直線)×2」という数式で記述したならば、ランナーは限りなく滑らかに・自然にトラックのカーブを走り抜けていくことができるはずなのです(下図の青線トラック)。
しかし、高速道路のカーブと同じように、トラックのカーブにおいて直線と円弧部分をクロソイド曲線で繋いでおいたならば、最初から最後まで曲率が滑らかに変化していきます。クロソイド曲線というものが、曲率を連続的に変化させていく曲線なので、曲率ゼロの直線と任意の有限曲率を持つ円弧の間を、クロソイド曲線は滑らかに繋ぐことができるわけです。
ということは、トラックを「(クロソイド曲線+円弧+直線)×2」という数式で記述したならば、ランナーは限りなく滑らかに・自然にトラックのカーブを走り抜けていくことができるはずなのです(下図の青線トラック)。
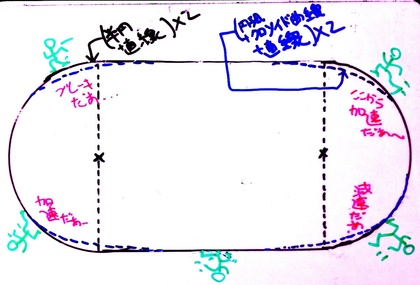
それにも関わらず、学校の校庭にあるトラックが、すべて(半円+直線)×2という数式でトラックが形作られているからには、きっとそれなりの理由があるのだろう、と思います。その理由を知りたい…というのが「この季節になると、いつも頭に浮かぶ疑問」なのです。
2012-08-02[n年前へ]
■数学ソフトウェア Geo Gebra でハロー・オッパイ! 
 数学ソフトウェア GeoGebra(説明)がなかなか面白そうなので(参考:Fallen Physicist, Rising Engineer)、夏の自由研究がてら、少し使い始めました。
数学ソフトウェア GeoGebra(説明)がなかなか面白そうなので(参考:Fallen Physicist, Rising Engineer)、夏の自由研究がてら、少し使い始めました。
どんな言語を使うときも、一番始めに書くべきコードは、Hello World! それはイコール「こんにちは赤ちゃん、私がママよ」という声に導かれ・この世に生まれ来る赤ちゃんが目にする景色、つまりは、(いつものように)ハロー・オッパイ!です。…というわけで、下に貼り付けたのは、「(各微小領域における)バスト重みと肌の張力が形作るオッパイ曲線」です。
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。
オッパイ星人の力学 第四回〜バスト曲線方程式 編
この動画は、オッパイの表面(境界)の各部分にかかる力を元に、張力を計算し、張力を曲率に(テキトーに)換算を行った上で、曲率=2階微分値を2階積分した結果をGeo Gebra でインタラクティブに図示した図を(大雑把に言えば)、パラメータを適当に動かすことでアニメーションにする…という具合で作られています。
使った数式は、下のようになります。あなたも、自分好みのHello World!ならぬハロー・オッパイを作り出してみるのは、いかがでしょうか?

左でスライダーを使ってパラメータ設定をしている部分は、きっと望ましくは(スライダーで調整するのではなく)「バストのX=0すなわち根元における傾き」を直線で表現し・その直線を動かし・調整する、という方が自然なのかもしれませんね。
2015-11-13[n年前へ]
■グラビアアイドルの肌を魅力的にする画像処理 
「愛川ゆず季」のグラビア写真を、さらに(個人の趣味はあれど)魅力的に美しく透明にしてみました。行った作業はとても簡単で、久保尋之らの"曲率に依存する反射関数を用いた半透明物体の…"を踏まえ、肌色領域を抽出した上、ランバート反射物体のコサイン関数に比例する輝度を分布を(RGBの波長違いを踏まえて)変化の少ない階調変換を掛けることで、グラビアアイドルの肌を魅力的にする画像処理を掛けてみた…という具合です。
下のモーフィング動画は、元画像を「魅力的画像」に変化させてみたものです。こうした処理は、昔から手作業で行われていたものと本質的に同じですが、そうした処理の原理・理屈を納得した上で行ってみると、結構面白く感じるものです。
ちなみに、この「グラビアアイドルの肌を魅力的にする画像処理」を倉持由香の写真に掛けて眺めたのがリンク先です。こうした機能を(人の好みに合わせたカスタマイズ機能付きで)ブラウザ標準機能にすると喜ばれるかもしれません。
2016-12-30[n年前へ]
■「π r2(パイアール2乗)=面積」式は、ひいらぎ愛 さんの乳曲率に適用可能か?問題 
「面積表示のタイトルがいいでしょ」というtweetに思わず目を引かれて、紹介文を眺めた途端に思わず笑ってしまいました。
「魅惑の巨大乳輪 ひいらぎ愛 π r2(パイアール2乗)=面積176cm2」巨大乳輪に特化した新シリーズです。第一弾は乳輪直径15cm、面積176cm2の…そして、ふと考えたのです。
「乳というものは、多くの場合は立体的な存在である。少なくとも、ひいらぎ愛さんの場合は、超立体的なものに違いない。それなのに、面積計算を2次元平面上の公式を使って良いものだろうか?」
そこで、果たしてπ r2(パイアール2乗)=面積176cm2で良いのかどうか、軽く計算をしてみることにしました。
ひいらぎ愛さんは、トップバストがバスト156cmでOカップということです。ということは、以前書いた おっぱい解析向けライブラリを使うと、彼女のトップバストに対してアンダーパストは45cm短い111cmであることがわかります。さらに、その乳を半球で近似した時の半径は30cmであると計算されます。
乳を半球で近似すると、乳輪の面積は「半球を乳輪の大きさである立体角θで切り取った領域の表面積」となり、式で書くと、
2π r^2 (1- Cos θ)となります。立体角θは、「乳輪直径15cm」というのが、表面に沿って長さを計ったものだとすると、乳輪の立体角θは約29度です。すると、その乳輪の表面積は172平方cmとなります。π r2(パイアール2乗)から計算される177平方cmとは、約5平方cmほど違います。最初の2桁だけを比べれば、曲率を考慮してもしなくても全く同じ数値ですから、その差は十分小さいのかもしれません。
「π r2(パイアール2乗)=面積」式は、ひいらぎ愛 さんの乳曲率に適用可能か?問題を解決するためには、その乳輪の直径だけでなく「円周の長さを計る」などの方法により乳表面の曲率を求める、という作戦が考えられます。それは、今後の課題としておこうかと思ます。

