2011-10-23[n年前へ]
■「トラック曲線=(半円+直線)×2」という運動会シーズンのナゾ!? 
 秋といえば運動会の季節です。この季節になると、いつも頭に浮かぶ「謎」があります。…それは「徒競走」をする校庭にある「トラック」の形に関する疑問です。
秋といえば運動会の季節です。この季節になると、いつも頭に浮かぶ「謎」があります。…それは「徒競走」をする校庭にある「トラック」の形に関する疑問です。
校庭のトラックは「両端の半円を直線で結んだ形」です。…はい、勘が鋭い人であれば、もう気づいただろうと思います。運動会シーズンにいつも考え込んでしまう謎というのは、なぜ
トラック曲線=(クロソイド曲線+円弧+直線)×2ではなくて、
トラック曲線=(半円+直線)×2なのだろう?ということなのです。
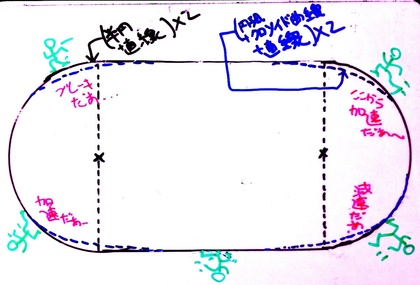
「トラック」の形状が「直線と半円」で形作られているとすると、直線コースから半円部分に突入した途端、急に、曲率がゼロからある程度大きな値に変わってしまいます。言うまでもなく、直線とは「曲率がゼロである」真っ直ぐな線であり、円とは曲率が一定の曲線であるからです。ということは、トラックを走るランナーたちは、体が進む方向を決める”ハンドル”をいきなり切らなければなりません(下図の黒線トラック)。
 しかし、高速道路のカーブと同じように、トラックのカーブにおいて直線と円弧部分をクロソイド曲線で繋いでおいたならば、最初から最後まで曲率が滑らかに変化していきます。クロソイド曲線というものが、曲率を連続的に変化させていく曲線なので、曲率ゼロの直線と任意の有限曲率を持つ円弧の間を、クロソイド曲線は滑らかに繋ぐことができるわけです。
ということは、トラックを「(クロソイド曲線+円弧+直線)×2」という数式で記述したならば、ランナーは限りなく滑らかに・自然にトラックのカーブを走り抜けていくことができるはずなのです(下図の青線トラック)。
しかし、高速道路のカーブと同じように、トラックのカーブにおいて直線と円弧部分をクロソイド曲線で繋いでおいたならば、最初から最後まで曲率が滑らかに変化していきます。クロソイド曲線というものが、曲率を連続的に変化させていく曲線なので、曲率ゼロの直線と任意の有限曲率を持つ円弧の間を、クロソイド曲線は滑らかに繋ぐことができるわけです。
ということは、トラックを「(クロソイド曲線+円弧+直線)×2」という数式で記述したならば、ランナーは限りなく滑らかに・自然にトラックのカーブを走り抜けていくことができるはずなのです(下図の青線トラック)。
それにも関わらず、学校の校庭にあるトラックが、すべて(半円+直線)×2という数式でトラックが形作られているからには、きっとそれなりの理由があるのだろう、と思います。その理由を知りたい…というのが「この季節になると、いつも頭に浮かぶ疑問」なのです。
2012-01-31[n年前へ]
■(ヤング率的に)かなりヤングな「おっぱい断面方程式」 
 美しい景色を見ると心動かされるように、美しい方程式を見ると感動します。そして、その方程式を見い出した人が持つ「力」に涙するものです。
美しい景色を見ると心動かされるように、美しい方程式を見ると感動します。そして、その方程式を見い出した人が持つ「力」に涙するものです。
今日は、「おっぱい断面方程式発見」というニュースに心動かされました。
@Xe_no: おっぱい断面方程式:x=3 y log[y]-1/36 exp[-(36y-36/e)^4] ( 0≦ y ≦1 )
もちろん、単に心動かされるだけでなく、自分でも「おっぱい断面方程式」をなぞってみたくなり、喜び勇んで?グラフにしてみました。それが、右に貼り付けたグラフです。
これは、「オッパイ古典力学研究者」としての感覚的には、そして力学的・ヤング率的には、「かなりヤングな断面」に思われます。
「おっぱい(曲面)方程式」とか、「美的曲線」基準の「理想バスト形状」とか、「オッパイ水風船曲線」とか、美しい方程式を求める努力は実に涙ぐましいものですよね…oπ。
参考:Wolfram Alpha版
2012-04-23[n年前へ]
■ぼくらが見慣れた2次方程式のグラフは…「胸の谷間」の方程式だった! 
 中学生か高校生の頃、XY平面の上にy=x^2+1といった2次方程式のグラフを描き、さらにそのXY平面の上にy=0という直線を描き、そのふたつのが交点を持たないので、x^2+1=0という方程式は実数解を持たない…という説明を聞いた覚えがあります。
中学生か高校生の頃、XY平面の上にy=x^2+1といった2次方程式のグラフを描き、さらにそのXY平面の上にy=0という直線を描き、そのふたつのが交点を持たないので、x^2+1=0という方程式は実数解を持たない…という説明を聞いた覚えがあります。
けれど、2次方程式の解の公式を解けば、そのy=x^2+1という方程式は2つの解、2つの複素数の解を何処かに持っている…という説明を聞きながら、何だか腑に落ちなかったような気がします。
先日、「複素数係数を持つ2次方程式の(複素数)解を”可視化する”エクセルシート」を作ってみましたエクセルで2次方程式の「解の配置」を図示してみる!?)。そして、x^2+1=0という方程式の解を眺めながら、ふとこんなことを思いました。
なんだ、これがぼくたちの探している青い鳥なんだ。
ぼくたちは、ずいぶん遠くまで青い鳥を探しに行ったけど…
本当は、いつもここにいたんだ。
複素空間上に、実に単純な2次方程式が描く曲面は、ふたつの(まるで胸のような)ふくらみを見せ、…x^2+1=0という方程式こそが、人を魅惑する何よりホンモノの「おっぱい曲面方程式」だったのではないか、と思ったのです。これまでに、たくさんの「おっぱい方程式」を眺めてきたけれど…x^2+1という思春期に眺めた式こそが、本当のおっぱい方程式ではなかったか…と気づいたのです。
 たとえば、下のグラフは複素空間上でx^2+1という式で求められる値と0という値の間の距離(ユークリッド・ノルム)を(縦軸を反転しつつ)描いてみたものです。つまり、それはx^2+1=0という方程式への「複素空間上での解への”近さ”」をグラフにしたものです。
たとえば、下のグラフは複素空間上でx^2+1という式で求められる値と0という値の間の距離(ユークリッド・ノルム)を(縦軸を反転しつつ)描いてみたものです。つまり、それはx^2+1=0という方程式への「複素空間上での解への”近さ”」をグラフにしたものです。
i(アイ)と-i(アイ)という虚軸上に頂(いただき)、すなわち解を位置させる「ふくらみ」は、それはまさに「おっぱい曲面」を感じさせます。…というより、これが「おっぱい」でなかったら、一体何だというのだ…という姿形をしています。けれど、この「美しい曲面」は、ただ複素空間上に描かれた ”x^2+1”というだけの曲面です。

そして、こんなグラフを眺めながら、…ぼくらが見慣れた実数で描かれたXY平面上の2次方程式のグラフは…複素空間上にあるはずの「おっぱい曲面」上に(ふたつの胸を分けるように)描かれた一本の曲線だった!…私たちが見慣れたあの曲線は「(魅惑の)胸の谷間の方程式」だった!と気づいたのです。
たとえば、上のおっぱい曲面を2分するように描かれた黒い線こしが、黒板の上に繰り返し眺めたはずの”y=x^2+1”という、単純で見慣れた2次曲線です。
 中学生の頃、黒板の上に見た「XY平面上に2次方程式のグラフ」は「胸の谷間の曲線」であったし、その魅惑曲線の向こうには複素空間上のおっぱい曲面があった…なんて、何だか凄いと思いませんか?
中学生の頃、黒板の上に見た「XY平面上に2次方程式のグラフ」は「胸の谷間の曲線」であったし、その魅惑曲線の向こうには複素空間上のおっぱい曲面があった…なんて、何だか凄いと思いませんか?
ふたつの胸のふくらみは、
何でもできる証拠なの。
「魔女っ子メグちゃん」
2013-01-24[n年前へ]
■シュワルツネッガー・ファインマン…あの有名人(の顔)曲線を、検索エンジンWolfram Alphaで描いてみよう! 
 数式処理ソフトMathematicaの開発元であるWolframが提供している検索エンジンWolfram Alphaでは、「有名人(の顔)曲線」を眺めることができます。たとえば、
Albert Einstein curveと検索すると、アルバート・アインシュタインの顔をパラメータ曲線として描いたグラフ画像を眺めることができます。
数式処理ソフトMathematicaの開発元であるWolframが提供している検索エンジンWolfram Alphaでは、「有名人(の顔)曲線」を眺めることができます。たとえば、
Albert Einstein curveと検索すると、アルバート・アインシュタインの顔をパラメータ曲線として描いたグラフ画像を眺めることができます。
今日は、そんな「有名人(の顔)曲線」の一覧を作ってみました。どの顔が「誰であるか」がわかるでしょうか?あるいは、どこかに隠れているはずの「アーノルド・シュワルツネッガー」を見つけ出すことができるでしょうか?

ちなみに、登場している人(曲線)たちは、Justin Bieber-like curve,Silvio Berlusconi curve,Wolf Blitzer curve,Charlie Chaplin curve,Anderson Cooper curve,Tom Cruise curve,Dalai Lama curve,Ellen DeGeneres curve,Paul Adrien Maurice Dirac curve,Albert Einstein curve,Richard Feynman curve,Bill Gates curve,Goethe curve,Che Guevara curve,Adolf Hitler curve,Angelina Jolie curve,Kim Jong Un curve,Lady Gaga curve,Jay Leno-like curve,David Letterman curve,Abraham Lincoln curve, curve,Marx-Engels-Lenin curve,Angela Merkel curve,Barack Obama curve,Barack Obama (with hair) curve,Conan O'Brien curve,PSY curve,Vlamidir Putin curve,Srinivas Ramanujan curve,Mitt Romney curve,Arnold Schwarzenegger curve,Josef Stalin curve,Stephen Wolfram curve,Howard Stern curve,John von Neumann curve,Oprah Winfrey curveといった具合です。そして、この画像群を作るためのMathematicaコードは
list = WolframAlpha["Person curve", "Result"];
result = Table[
a = (WolframAlpha[#, "PodCells"][[2]]) &@
(list[[#]]) & @@ {i};
Export["temp.jpg", a];
ImageCrop[Image@Import["temp.jpg"],
{210, 210}, {Right, Bottom}]
, {i, 1, Length@list}]
といった具合です。
2013-02-16[n年前へ]
■Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ 
 数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
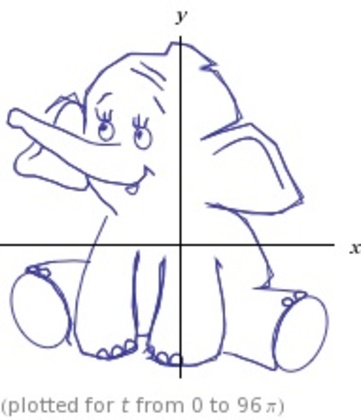
「ゾウさん曲線」あるいは
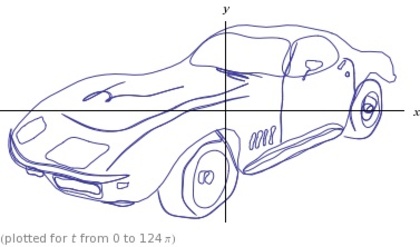
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?
数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
「ゾウさん曲線」あるいは
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?

実は、こういった「画像を表現するパラメータ曲線(群)」は、(かなりの部分を)自動的な作業により、比較的簡単に作り出すことができます。
それはこのような手順です。

- (通常画像から自動生成する場合)画像を白黒濃淡(グレー)画像にして、(少し画像をぼかした上で)濃淡値の等高線を作る
- (通常画像から自動生成する場合)各等高線は(画像境界部などの例外を除けば)閉曲線になっているので(等高線が途切れたりすることはないですから)、各閉曲線をフーリエ記述子で表現する
- (イラストから生成する場合)複数曲線からなるイラストを作り、各曲線をフーリエ記述子で表現する
- 各曲線を表現するフーリエ記述子の低次の項(低次の3角関数)だけ抜き出し、リストにする(並べる)
- …それらのパラメータ曲線群を並べたもの=任意の図形を描き出す曲線の集合になる
 「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
そして、そんな(単純のために閉曲線であるとします)閉曲線を描き出す(1周するごとに周期関数となる)パラメータの動きをフーリエ変換することができますから、結局のところ3角関数を重ね合わせたものをパラメータにして表現される曲線として、任意の(閉)曲線を表すことができる…というわけです。これが図形のフーリエ記述子による表現です。
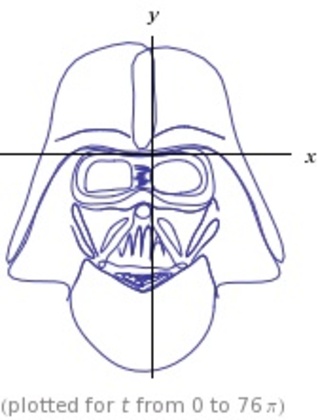 さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
これがWolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピです。…作り方を眺めてみれば、あまり「意味や価値・美しさのない曲線(存在)」に思えてしまうかもしれませんね。