2013-02-16[n年前へ]
■Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ 
 数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
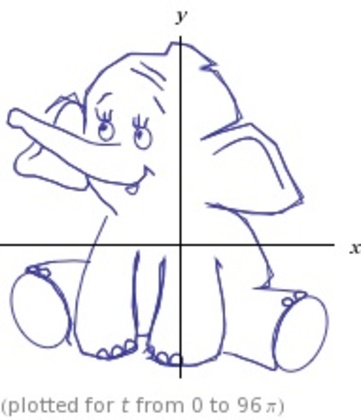
「ゾウさん曲線」あるいは
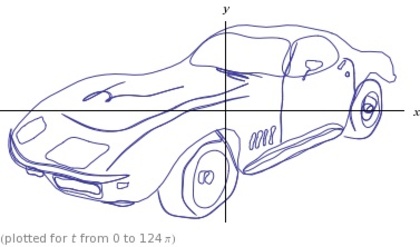
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?
数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
「ゾウさん曲線」あるいは
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?

実は、こういった「画像を表現するパラメータ曲線(群)」は、(かなりの部分を)自動的な作業により、比較的簡単に作り出すことができます。
それはこのような手順です。

- (通常画像から自動生成する場合)画像を白黒濃淡(グレー)画像にして、(少し画像をぼかした上で)濃淡値の等高線を作る
- (通常画像から自動生成する場合)各等高線は(画像境界部などの例外を除けば)閉曲線になっているので(等高線が途切れたりすることはないですから)、各閉曲線をフーリエ記述子で表現する
- (イラストから生成する場合)複数曲線からなるイラストを作り、各曲線をフーリエ記述子で表現する
- 各曲線を表現するフーリエ記述子の低次の項(低次の3角関数)だけ抜き出し、リストにする(並べる)
- …それらのパラメータ曲線群を並べたもの=任意の図形を描き出す曲線の集合になる
 「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
そして、そんな(単純のために閉曲線であるとします)閉曲線を描き出す(1周するごとに周期関数となる)パラメータの動きをフーリエ変換することができますから、結局のところ3角関数を重ね合わせたものをパラメータにして表現される曲線として、任意の(閉)曲線を表すことができる…というわけです。これが図形のフーリエ記述子による表現です。
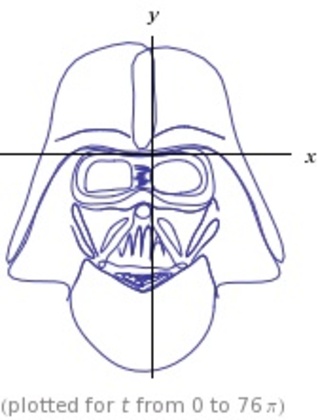 さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
これがWolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピです。…作り方を眺めてみれば、あまり「意味や価値・美しさのない曲線(存在)」に思えてしまうかもしれませんね。