2001-02-16[n年前へ]
■言って後悔するくらいなら… 
言わなきゃいいのに。というわけで、言ってしまって気になっていたことを謝る。
2002-02-16[n年前へ]
■今日思い出したこと 
日々の雑記帳の'02/02/12のCNNの話を読んで、「今日のできごと」を思い出した。そういえば、きょうNさんに「WEB更新復帰のこんな話どう思う?」と聞かれ、そのページの原案を読んだ。
下丸子にいた頃、私のデスクトップでこっそり動かしはじめたhttpサーバーもいつのまにか公式なサーバーに変わり管理者も代わり、そして部署名やいろいろなことが変わった今は「公式なんだろうけど、なんかよくわからないサーバー」になっている。
そういえば、「できるかな?」をこっそり書きはじめたのもあのサーバーの中だった。最初の頃の話は今でもあのサーバーの中で見ることができる。うーん、社内の何人かの同僚にメールで更新報告を送りつけていた頃が懐かしいぞ、と。
それにしても、リコー有志による「英語技術文献の日本語要約」はまだまだ続く。えらいのである。ということで、今日のポストイットは変更してみよう。(リンク)(リンク)
2003-02-16[n年前へ]
■こころやすらぐソロギター リラクゼーション・ミュージック Vol.1 
ヤマハミュージックメディア。ギター編曲、江部賢一。まずは「世界の車窓から テーマ曲」を練習してみようかな。CDもついてるし、楽譜は眺めるだけで音楽を聴くだけでも結構お勧めだと思う。
ガットギターの小さいサイレントギターを探してみよう。AriaのAS-100C/SPLにでもしてみようかな。ナット幅43mmだとまずいかな?どうかな?
■POV-Rayプラグイン 
PhotoshopからPOV-Rayのレンダリング機能を使って、三次元画像を描くプラグインの叩き台を作る。三次元ロゴもこれで、ね…。
■「≠腐ったミカン」 
あの記事は好きだけれど、「腐ったミカン」は現場監督、というタイトルはキライ。「」がついてるにせよ、短くしたいにせよ、あるいはタイトルを付けたのは記者じゃないかもしれないにせよ、そのタイトルの付け方は違うんじゃないの、と思う。「腐ったミカン」じゃないから現場監督、なんじゃないのと思ったり。
ただ、それであっても早川健人という記者の名前は覚えておこうと思う。
2004-02-16[n年前へ]
■青空検索 
繰り返す過ちのその度人はただ青い空の蒼さを知る「いつも何度でも」 覚和歌子空という言葉で検索をかけると、ずいぶんと多く「空」が見つかる。「青空」だけでも結構ある。まだ数年分だけれども、そんな「空」を集めてみるのも面白いかも。
2005-02-16[n年前へ]
■「小さな世界」 
 「あなたが思っているより、世界は小さいかもね」という"Small World"
「あなたが思っているより、世界は小さいかもね」という"Small World"
全球写真を足下を中心に撮影することで、まるで「星の王子さま」の星みたいに世界を描いた写真の数々。ビルが林立する小さな星や、誰かの部屋の小さな部屋や、近くの公園の小さな星、とか。 from SLN:blog*
2008-02-16[n年前へ]
■「鯖街道」と「地獄八景亡者戯」 
NHK朝の連続テレビ小説「ちりとてちん」で、涙なくしては見ることができない「地獄八景亡者戯」が演じられている。何週間かかけて、何人もの登場人物たちが、それぞれの人生に重ねた「地獄八景亡者戯」を演じる。その幾重にも重なる人生の姿に涙する人は多いと思う。
冥途を旅する……という話のルーツは随分古いものがありましょうが、これを滑稽なしゃれのめした物語にしたのは、(室町の狂言にもありますが)やはり江戸時代からでしょう。
「地獄八景亡者戯」は、鯖にあたって死んだ「喜ぃさん」の話で始まる。若狭の海から京都・大阪へと鯖を運んだ街道が鯖街道・若狭街道だということを思い返せば、何だか「地獄八景亡者戯」はとてもその鯖街道と似合ってる。
もともとこの話は、その時その時の事件や世相流行などをとり入れて、言わばニュース性を持たせてやる演出で伝わってきたものです。五世笑福亭松鶴師のは、私が聞いたのは戦後でしたが、昭和初期の赤い灯青い灯の道頓堀、カフェー全盛時代や、活弁の真似なんかがはいっていました。
このはなしの一応の原典と見てよいものは江戸時代の小咄本にありますが、各地の民話にもあり、また欧州の民話にもあるそうで、木下順二氏の「陽気な地獄破り」はこのヨーロッパの民話を基にされています。本当の原典は従ってよく判らないというのが答えと言えましょう。
小浜の町から若い(わかい)主人公 若狭(わかさ)が関西の街へ出て、年を重ねつつ色んなものを見る。そんな話と「鯖街道」と「地獄八景亡者戯」は、とても自然に重なっている。
その内に、これを十八番の持ちネタとして新しい「地獄八景」を作ってくれる人が出てくることでしょう。これは滅ぼしたくない話です。
2009-02-16[n年前へ]
■「機械制御工学」のススメ 
 制御工学の本は、読んでいて面白いものも多い。もちろん、そんな本の数は半分以下ではあるけれど、制御に関するさまざまなエピソードを紹介しつつ、制御の理論と実践を解説してくれる本がある。
制御工学の本は、読んでいて面白いものも多い。もちろん、そんな本の数は半分以下ではあるけれど、制御に関するさまざまなエピソードを紹介しつつ、制御の理論と実践を解説してくれる本がある。
金子敏夫の「機械制御工学
」はそんな本の一つで、これまで読んだ制御工学本の中でも、特に「フィードバック制御の発祥から発展と解析」を説明する数章に関しては、一番面白かった。
たとえば、実に充実した制御技術発達の経緯についての年表もあり、水洗トイレのタンク水量調整に使われる浮子を用いたタンク液面制御は1750年に作り出されたことがわかったり、1776年にはアダム・スミスが国富論の中でフィードバックの考えを記述し、さらに次の年、1787年には蒸気機関の調速機と同じ原理の、製粉用ガバナ付リフトテンダが発明されていることがわかる。
情けない話だが、この本を読んでようやくラプラス変換のS空間が頭の中に直感的にイメージできるようになった。もしも、ラプラス変換が「公式としてはわかるけど…」と思う人は、立ち読みしてみても損はないと思う。
2010-02-16[n年前へ]
■「コンドーム」開発秘話に涙しろ (初出:2006年08月11日) 
 昼休みに外を散歩していると、ゴム風船のようなものが落ちていました。男性のアレにつけるゴム風船、つまりは、コンドームが落ちていたのです。箱根の山中というロマンチック?な場所柄、そんなグッズが転がっていることもよくあります。
昼休みに外を散歩していると、ゴム風船のようなものが落ちていました。男性のアレにつけるゴム風船、つまりは、コンドームが落ちていたのです。箱根の山中というロマンチック?な場所柄、そんなグッズが転がっていることもよくあります。
ダッチワイフの下半身部分だけが転がっていたこともありますが(最初は死体かと思ってビックリした)、さすがにゴム人形と対面したのは一度だけです。
 コンドームと言えば、コンドームの代名詞ともなっているオカモト株式会社(オカモトコンドーム)が自社WEBサイトに掲載している「世界最高品質のコンドーム開発秘話~40ミクロンの壁を突破せよ!~」は必見です(2010年現在では、下記の本でしか読むことはできません)。「栄光なき挑戦者たち~NHKには絶対できないもうひとつのプロジェクトX~」という本に収録もされている文章で、一見"プロジェクトX"のパロディに見えるタイトルです。しかし、内容はパロディどころか、本家"プロジェクトX"を遥かに超えていて、ちょっと眺め始めた途端、
コンドームと言えば、コンドームの代名詞ともなっているオカモト株式会社(オカモトコンドーム)が自社WEBサイトに掲載している「世界最高品質のコンドーム開発秘話~40ミクロンの壁を突破せよ!~」は必見です(2010年現在では、下記の本でしか読むことはできません)。「栄光なき挑戦者たち~NHKには絶対できないもうひとつのプロジェクトX~」という本に収録もされている文章で、一見"プロジェクトX"のパロディに見えるタイトルです。しかし、内容はパロディどころか、本家"プロジェクトX"を遥かに超えていて、ちょっと眺め始めた途端、
という第一章から、初めてコンドームを吉原の遊廓に持っていったときのことだった。それを見て、吉原のお姐さんはウンザリした表情でこう言った。「使えば、オソソ(陰部)が傷つく。使わなければ梅毒で鼻がもげる。さてさて、どっちを選ぶべきか。ま、どっちを選んでも地獄だわねえ」
という最終章まで、とても真剣に読んでしまうだろうと思います。今日、世界に冠たる日本の製造業は、中国やインドなどの猛追で喘いでいる。トップメーカーは相次いで外国に生産拠点を移し、産業の空洞化も懸念されている。文部科学省は日本人の創造性を高めようと、「ゆとり教育」を導入した。
会社は、そこで働く者すべてのもの。経営者も従業員より偉い存在ではない。ただ社長は企業の方向性を考える役割を与えられているだけ。
 そういえば、以前八方尾根スキー場で「ポシェットの落とし物が届きました。男性向けのデザインで、はオカモトさんが中に入っています。心当たりの方は、案内所までお越し下さい」というアナウンスを聞いたことがあります。
そういえば、以前八方尾根スキー場で「ポシェットの落とし物が届きました。男性向けのデザインで、はオカモトさんが中に入っています。心当たりの方は、案内所までお越し下さい」というアナウンスを聞いたことがあります。
「ポシェットに人が入ってるの?」と誰もが一瞬首を傾げた後、「あぁ!(コンドームか!)」と周りで失笑・爆笑が起こりました。まさに、「考えオチ」です。オカモトさんの持ち主は、あの後どうしたんでしょうか。
2011-02-16[n年前へ]
■「たどり着く」ための「3つの力」 
「3つの力」を手に入れたいなと腹黒く思うことがあります。・・・神を恐れぬ「3つの力」をギリシャ神話風に言えば、それは「背の高い草が生える海岸近くに立つ古い灯台から、海岸に辿り着くために必要な3つの力です。
 「3つの力」のひとつめは、「灯台の上から、海岸に向かう方向を見極める力」です。背の高い草の中に入ってしまえば、方向を見失い、どの方向に進んだら良いのかわからなくなります。けれど、そんな中でも灯台の上から眺めれば、草原を抜けて海岸まで辿り着くために向かえば良い方向がわかります。そんな「灯台の上から草原の上を抜けて浜辺までの道のりを見極める・見通す力」です。
「3つの力」のひとつめは、「灯台の上から、海岸に向かう方向を見極める力」です。背の高い草の中に入ってしまえば、方向を見失い、どの方向に進んだら良いのかわからなくなります。けれど、そんな中でも灯台の上から眺めれば、草原を抜けて海岸まで辿り着くために向かえば良い方向がわかります。そんな「灯台の上から草原の上を抜けて浜辺までの道のりを見極める・見通す力」です。
ふたつめは、「背の高い草むらの中を歩く力」です。目の前にある草を刈り、着実に前へと進んで行くちから」です。もしかしたら、それは「実装力」といったものと似ているのかもしれません。
 そして、みっつめが「その方向に進むことには価値があると築く力」です。「あの方角にはきっと何かがある、歩き続けることには価値がある」と感じさせるための力です。…そんな方角にいるだろう客を見つけ、そんな人たちと自分たちを繋ぐ力です。時にそれを人は「営業力」と呼びます。
そして、みっつめが「その方向に進むことには価値があると築く力」です。「あの方角にはきっと何かがある、歩き続けることには価値がある」と感じさせるための力です。…そんな方角にいるだろう客を見つけ、そんな人たちと自分たちを繋ぐ力です。時にそれを人は「営業力」と呼びます。
…といっても、大層な話しではなくて、これらみっつのすべてを人はみんな備えていることが多いに違いないと思っています。つまり、誰もが備えているだろう力を、自分も人並みに欲しい・手に入れたいと贅沢にも考えたりします。
2012-02-16[n年前へ]
■「教室の黒板を夕日が照らす」のは「マンガの中だけの話」です!? 
 学生の可能性を可能にするポータルサイト ワンダーノーツに「教室の黒板を夕日が照らす」のは「マンガの中だけの話」です!?を書きました。
学生の可能性を可能にするポータルサイト ワンダーノーツに「教室の黒板を夕日が照らす」のは「マンガの中だけの話」です!?を書きました。
「夕日が(今日の”日直”の名前が書かれた)教室の黒板を照らす」という風景は、マンガなどでよく描かれそうなノスタルジックな景色です。 …しかし、そんな「夕日に照らされた黒板」は、現実には(あまり)存在しない風景です。 なぜなら、学校の(多くの)教室は、黒板に夕日が当たることがない向きで作られているからです。
100年以上前の明治28年、当時の文部省が「学校建築図説明及設計大要」というものを発行しました。 これは、学校を作る際には「こういう風に作りなさい」という指導書です。 この「学校建築図説明及設計大要」では、(特殊な教室でない)普通教室について、次のように「教室・窓の向き」が決められています。
2013-02-16[n年前へ]
■Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ 
 数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
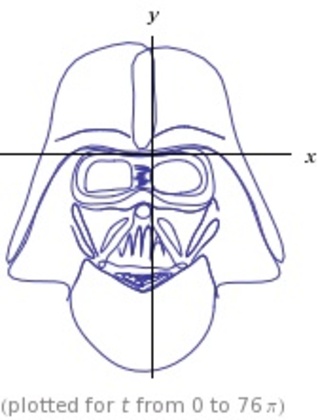
「ダースベーダー曲線」や
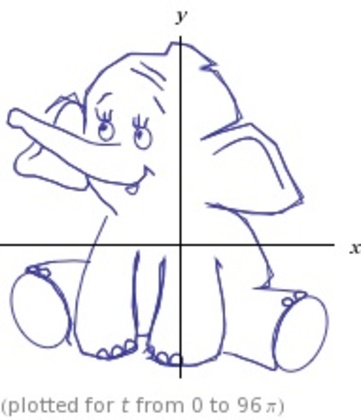
「ゾウさん曲線」あるいは
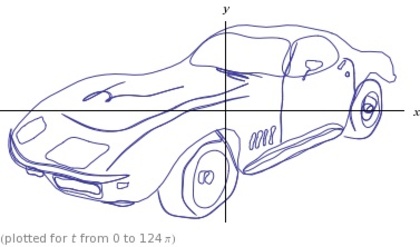
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?
数式処理ソフトMathematicaの開発元であるWolframが提供している知識検索エンジンWolfram Alphaは、さまざまな有名人の顔を表現する「曲線(パラメータ関数)」を作り出すことができます。そして、それだけでなく、
「ダースベーダー曲線」や
「ゾウさん曲線」あるいは
「車のコルベット曲線」「スーパーボール曲線」「PSY曲線」
といった、ありとあらゆるものを描き出す曲線を眺めることができます。
…そんな都合良く「図形を表す」曲線群は、一体どのようにして作り出されているのでしょうか?

実は、こういった「画像を表現するパラメータ曲線(群)」は、(かなりの部分を)自動的な作業により、比較的簡単に作り出すことができます。
それはこのような手順です。

- (通常画像から自動生成する場合)画像を白黒濃淡(グレー)画像にして、(少し画像をぼかした上で)濃淡値の等高線を作る
- (通常画像から自動生成する場合)各等高線は(画像境界部などの例外を除けば)閉曲線になっているので(等高線が途切れたりすることはないですから)、各閉曲線をフーリエ記述子で表現する
- (イラストから生成する場合)複数曲線からなるイラストを作り、各曲線をフーリエ記述子で表現する
- 各曲線を表現するフーリエ記述子の低次の項(低次の3角関数)だけ抜き出し、リストにする(並べる)
- …それらのパラメータ曲線群を並べたもの=任意の図形を描き出す曲線の集合になる
 「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
「フーリエ記述子での表現」というのは、簡単にいうと次のようなことです。(模様を描き出す)閉曲線がある時、その閉曲線を「何らかのパラメータにより表されている曲線だ」と考えてみることにします。たとえば、原点を中心にして「半径というパラメータが増減する」閉曲線を考えてみれば、それは「星形のような模様を1周するごとに描き出す(描くことを繰り返す)曲線(カーブ)」になります。あるいは曲線を(最初の位置からの)角度変化といったパラメータなどで表すこともできるでしょう。とにかく、そんな風に曲線を、(関数を固定して)変化するパラメータで表現されるパラメータ曲線だと考えてみるのです。
そして、そんな(単純のために閉曲線であるとします)閉曲線を描き出す(1周するごとに周期関数となる)パラメータの動きをフーリエ変換することができますから、結局のところ3角関数を重ね合わせたものをパラメータにして表現される曲線として、任意の(閉)曲線を表すことができる…というわけです。これが図形のフーリエ記述子による表現です。
 さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
さらに、フーリエ変換された(周期関数である)パラメータを3角関数の低次の項だけで表せば(高次の3角関数を省略すれば)、高周波数成分が消えて、滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になるのです(式も短くなりますしね)。それが、結局のところ、Wolfram Alphaが作り出す「さまざまな曲線」になります。実際、「表示されている曲線を示す関数リスト」を眺めてみると、3角関数で表されていることがわかります。
これがWolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピです。…作り方を眺めてみれば、あまり「意味や価値・美しさのない曲線(存在)」に思えてしまうかもしれませんね。
2014-02-16[n年前へ]
■雪だるまにおける放射性炭素年代測定(C14)法 
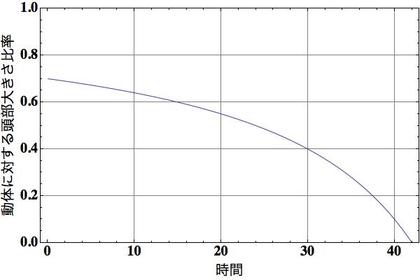
 雪降り後に街に残る雪だるまは、頭と胴体の大きさ比率を見れば、作られてからの時間経過を推定することができます。なぜかというと、雪だるまの丸く球形状の胴体や頭部が解けていくスピードはその表面積に比例するので(それを言い換えると、時間当たりの半径減少量は半径に寄らず一定だということになります)、時間が経過するにしたがって胴体に対して頭部が小さくなっていくからです(下図のグラフ参照)。
雪降り後に街に残る雪だるまは、頭と胴体の大きさ比率を見れば、作られてからの時間経過を推定することができます。なぜかというと、雪だるまの丸く球形状の胴体や頭部が解けていくスピードはその表面積に比例するので(それを言い換えると、時間当たりの半径減少量は半径に寄らず一定だということになります)、時間が経過するにしたがって胴体に対して頭部が小さくなっていくからです(下図のグラフ参照)。
 雪だるまの理想的なプロポーションは、頭部の大きさが胴体の7割くらいです。そのプロポーションが、雪だるまが作られてから時間が経つにしたがい、頭部が小さくなっていくわけです。ちょうど、化石などの年代推定を放射性炭素年代測定(C14)法で行うように、街中で見かけた雪だるまのプロポーションを「(作成時の)理想的な雪だるまプロポーション=頭部は胴体の70パーセント」と比べることで、雪だるまの年齢を推定することができるというわけです。
雪だるまの理想的なプロポーションは、頭部の大きさが胴体の7割くらいです。そのプロポーションが、雪だるまが作られてから時間が経つにしたがい、頭部が小さくなっていくわけです。ちょうど、化石などの年代推定を放射性炭素年代測定(C14)法で行うように、街中で見かけた雪だるまのプロポーションを「(作成時の)理想的な雪だるまプロポーション=頭部は胴体の70パーセント」と比べることで、雪だるまの年齢を推定することができるというわけです。