2014-05-27[n年前へ]
■エクセルでラプラス方程式を解いて「血管がある皮膚周りの光強度分布」を計算してみよう!? 
 赤い血が流れているはずの血管が青く見える理由で行った計算を大雑把に解けば、たとえば完全拡散体として扱うことができます。それはすなわち、任意の微小領域が周囲に発する光強度は周囲(の微小部分が発する光強度)の平均値になるということで、つまりはラプラス方程式で表される解になります。
赤い血が流れているはずの血管が青く見える理由で行った計算を大雑把に解けば、たとえば完全拡散体として扱うことができます。それはすなわち、任意の微小領域が周囲に発する光強度は周囲(の微小部分が発する光強度)の平均値になるということで、つまりはラプラス方程式で表される解になります。
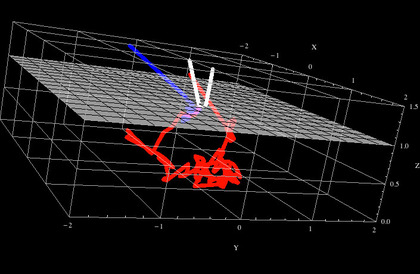
…というわけで、ラプラス方程式を離散化して、お手軽なエクセルで「皮膚内部に血管がある時の、その周辺の皮膚内部・表面での光強度分布を(たとえば青色波長で)可視化してみたのが下図になります。エクセルの各セルは離散化された空間上の各領域を示していて、そこに示されている色と値が光強度を示しています。
画面真ん中辺りに(画面=シート鉛直方向に)血管が流れていて、画面=シート上側にあたるのが皮膚表面です(画面下側が皮膚最奥部です)。

さらに青色・赤色波長の「(光が散乱して方向を変えるまでの)平均自由行程」を踏まえて、表面での光強度分布の違いを描いてみると、限りなく大雑把な近似に基づいた計算をすると、下図のような感じです(縦軸はその波長における周辺近傍の平均強度を基準にした相対値です) 。
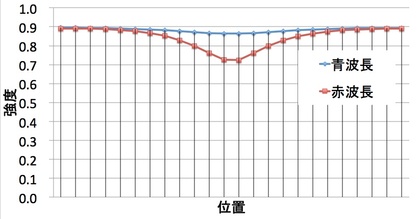
血管が下部にある部分を眺めると、青色波長では、その周囲の部分とさほど変わらない光を発しています。けれど、そこを赤色波長で眺めれば(表皮近くの毛細血管ではなく)皮膚下部に流れる血液に光が吸収されて、光強度が(近傍周囲より)減少していることがわかるかと思います。…だから、赤い血が流れているはずの血管が(周囲に対して相対的に)青く見える、というわけです。
2017-09-01[n年前へ]
■下着マチ部分の「わずかな凹凸」がなぜボトムスの上から視認されるのか? 
平日のラッシュ時間、駅のホームから上がる階段は、人がギュウギュウに詰まっている。 その階段を登りながら、こう考えた。
 職場や学校に向かうだろ多くの人に挟まれて、密度高く窮屈に階段を昇っていると、ちょうど1メートルくらい先の正面に、階段を上る女性がいる。
私の顔のちょうど正面に彼女のヒップがあるせいか、それとも何か他のユング心理学的な何か深層心理の原因があるせいか、とにかくその球面状のヒップが目に入る。
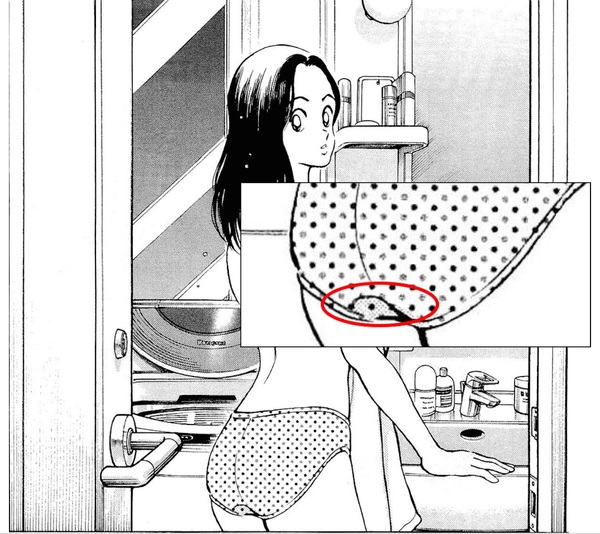
もしかしたら、そのヒップが気になったのは、下着の線が浮かび上がっていたせいかもしれない。
女性はストレッチ素材のボトムス(ズボン)をはいていて、階段を昇るために足を上げる動作をするせいか、ボトムスに明瞭に下着の線が浮き上がっている。
それは、下着のアウトラインだけでなく、股部分の左右を繋ぐ「マチ」も線となり浮き上がり、それはまさにあだち充が描く「ムフ♡!」的な気持ちを思い起こさせた。
職場や学校に向かうだろ多くの人に挟まれて、密度高く窮屈に階段を昇っていると、ちょうど1メートルくらい先の正面に、階段を上る女性がいる。
私の顔のちょうど正面に彼女のヒップがあるせいか、それとも何か他のユング心理学的な何か深層心理の原因があるせいか、とにかくその球面状のヒップが目に入る。
もしかしたら、そのヒップが気になったのは、下着の線が浮かび上がっていたせいかもしれない。
女性はストレッチ素材のボトムス(ズボン)をはいていて、階段を昇るために足を上げる動作をするせいか、ボトムスに明瞭に下着の線が浮き上がっている。
それは、下着のアウトラインだけでなく、股部分の左右を繋ぐ「マチ」も線となり浮き上がり、それはまさにあだち充が描く「ムフ♡!」的な気持ちを思い起こさせた。
人が何に「ムフ♡!」を感じるかは、それはまさに個性で、その人次第に違いない。 けれど、私の場合は、下股部分の左右を繋ぐ、上を凸とする「マチ」の円弧状の曲線に、「ムフ♡!」を感じるらしい。それはもしかしたら、あだち充ではなくて、桂正和の影響だったのかもしれない。
 そこまで考えが漂流してきた時に、こんな疑問が湧いてくる。
「なぜ、下着のマチ部分を、ボトムスの上から見ることができるのだろう?」
「マチ部分には確かに凹凸ができるだろうけど、それほど大きくなさそうな凹凸を、なんで視認することができるのだろう?」
そこで、目の前のヒップを観察しながら階段を登りつつ考えた。
そこまで考えが漂流してきた時に、こんな疑問が湧いてくる。
「なぜ、下着のマチ部分を、ボトムスの上から見ることができるのだろう?」
「マチ部分には確かに凹凸ができるだろうけど、それほど大きくなさそうな凹凸を、なんで視認することができるのだろう?」
そこで、目の前のヒップを観察しながら階段を登りつつ考えた。
下着のマチ部分は、他の部分に比べて約2ミリメートルくらい厚い。 つまり、女性の丸いお尻が下着をはくと、丸い曲面上に「下着のマチ」という高さ約2ミリメートル程度の山脈ができる。
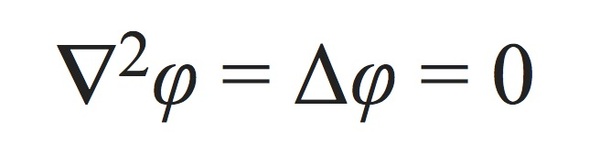 そんな山を持つ曲面面を、さらにストレッチ素材のボトムスが覆うとき、収縮しようとするストレッチ素材の生地を支配する方程式は、ポテンシャル曲面は可能な限り「滑らか」になるというラプラス方程式である。
つまり、下着のマチ部分を覆うストレッチ素材のボトムスがどう見えるかを考えるときには、ラプラス方程式の解を求めればよい。
そんな山を持つ曲面面を、さらにストレッチ素材のボトムスが覆うとき、収縮しようとするストレッチ素材の生地を支配する方程式は、ポテンシャル曲面は可能な限り「滑らか」になるというラプラス方程式である。
つまり、下着のマチ部分を覆うストレッチ素材のボトムスがどう見えるかを考えるときには、ラプラス方程式の解を求めればよい。
自然界の多くの現象がラプラス方程式を使って解くことができるように、下着のマチ厚みが作るボトムス表面形状を、ラプラス方程式で求めることにしよう。…そのために、まずは、下着のマチ部分あたりの女性のヒップを、直径8センチメートルの球面形状だとしてみる。 すると、ラプラス方程式の解を概算すると、下着のマチ部分のストレッチ素材のボトムスは、ざっくり「高さ2ミリメートルで、両側になだらかな斜面が約9ミリメートルほどつづく山(凸形状)」ができることになる。
すると、次の疑問がさらに湧く。
「高さ2ミリメートルで、両側になだらかな斜面が約9ミリメートルほどつづく山(凸形状)」を人は視認することができるものだろうか?
約1メートル離れて、視線方向への2ミリの凹凸となると、両眼視差で形状を捉えるようなスケールではない。 となると、そのオフホワイト単色のボトムスに浮かぶ凹凸を識別する手掛かりは、陰影情報だけだろう。
 物体に照明があたるとき、その表面の陰影はコサイン(照明角度)で表される。
ということは、高さ2ミリメートルの下着マチ山脈の陰影は、「両側に約9ミリメートル続くなだらかな斜面」の角度(斜度)を計算し、そのコサインを評価してやれば良いことになる。
ちなみに、下着マチ山脈の斜度を計算してみると、約13度だ。
照明が約45度方向から照らすなら、下着マチ山脈の片側斜面は(他の部分より)約8パーセント明るく、もう片側の斜面はその逆に約8パーセント暗いということになる。
物体に照明があたるとき、その表面の陰影はコサイン(照明角度)で表される。
ということは、高さ2ミリメートルの下着マチ山脈の陰影は、「両側に約9ミリメートル続くなだらかな斜面」の角度(斜度)を計算し、そのコサインを評価してやれば良いことになる。
ちなみに、下着マチ山脈の斜度を計算してみると、約13度だ。
照明が約45度方向から照らすなら、下着マチ山脈の片側斜面は(他の部分より)約8パーセント明るく、もう片側の斜面はその逆に約8パーセント暗いということになる。
 人の視覚が濃淡模様を識別する特性を考えると、約1メートル離れた9ミリメートルピッチつまり角度約1度の濃淡模様は、数十分の1程度でも識別することができる。
つまり、下着マチ部分の濃淡は、その高さがわずか2ミリメートルだとしても、明瞭に視認されることになる。
もちろん、いわゆる視力的にも角度約1度は約0.02に相当するから、全くもって問題は無い。
結局のところ、「下着のマチ部分の凹凸はわずかでも、その陰影は視認するのに十分な濃淡になる」ということになる。
人の視覚が濃淡模様を識別する特性を考えると、約1メートル離れた9ミリメートルピッチつまり角度約1度の濃淡模様は、数十分の1程度でも識別することができる。
つまり、下着マチ部分の濃淡は、その高さがわずか2ミリメートルだとしても、明瞭に視認されることになる。
もちろん、いわゆる視力的にも角度約1度は約0.02に相当するから、全くもって問題は無い。
結局のところ、「下着のマチ部分の凹凸はわずかでも、その陰影は視認するのに十分な濃淡になる」ということになる。
と、考えがさらにここまで漂流してきた瞬間、駅の階段を踏み損なって転びかけた。足の先を強く打ち痛い思いはしたけれど、幸い何ともなかった。 階段を昇る目の前の女性のヒップに浮かぶ「ムフ♡!」を眺めつつ、考えごとをすることは、有意義と言うよりは少し危険なことなのかもしれない。