hirax.net::Keywords::「ラプラス方程式」のブログ

トップページ"hirax.net" へ　/　サイトBlog "inside out" へ

「ラプラス方程式」に関する最新記事　/　「ラプラス方程式」に関する「説明」「記事の一覧」
| より古い5件の記事へ | より新しい5件の記事へ

2008-07-22[n年前へ]

■エクセルでシミュレーション Vol.5 [冷たく美味しい湧水編]　

　暑い夏空の下、私たちが立つ地面の遥か奥底で流れる地下水が、長い時間をかけ湧水地にまで流れてくるようすを眺めてみたくなりました。そこで、そんなシミュレーション計算をしようとエクセルでシミュレーション Vol.4 [定常理想流体準備編]で計算の準備をしてみました。

　というわけで、準備したワークシートが下の画像です。左上に山腹の高原湖があって、右下には海辺近くにある湧水群がある、という具合です。右上半分は青空で、一番下の列は固い岩盤が水を遮っている、というのがこのエクセルのセルで描かれたモザイク画です。

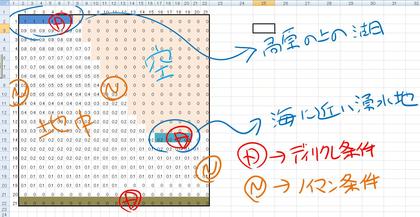
　上のような状態で、定常な理想流体のポテンシャル流れを計算してみた結果が、下の図になります。左上の湖水が地中に沁みわたり、ゆっくりと時間をかけて冷えて漉されて美味しい水となって、湧水地に辿り着くまでの姿が見えてくるような気がします。

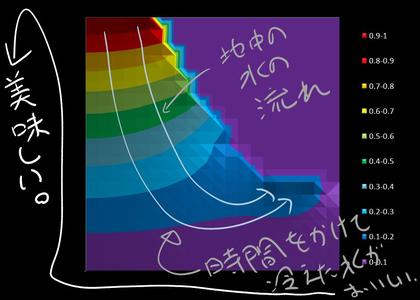
　エクセルのグラフからは見えてこないかもしれませんが、富士の近くで眺める湧水は本当に澄んでいます。空の色を少し映して、ほんのりと水底を青緑色に染め、その上の水面に夏の青空と白雲を重ねた、そんな景色を見せています。

この記事の「関連お勧め記事」を読む >>

2008-08-06[n年前へ]

■エクセルでシミュレーション Vol.7 「吉野家の法則編」　

　「安い」「早い」「旨い」を兼ね備えたものは売れる、というのが「吉野家の法則」の第１法則である。けれど、それら３つのことは相反することが多いために（「吉野家のジレンマ」）、それら３つのうち最低２つのものがあれば売れることが多い、というのが「吉野家の法則」の第２法則だ。

　「表計算でシミュレーション」というお題で、この吉野家の法則の「安い」「早い」「旨い」を考えてみよう。

　まずは「安い」である。それを言いかえれば、「簡単に手に入れることができる」ということだ。まず、「表計算でシミュレーション」はこの「安い」という条件を非常に上手く満たしている。

表計算ソフトウェア・エクセルを持っている人は多いから、必要な道具を手に入れることが簡単である。

　また、必要なものは決して道具だけでなく、その作業をするための理解力なども必要とされる。その理解に払うための労力・コストも、「表計算でシミュレーション」では安い。なぜなら、離散化された空間が表計算ソフト上のセルとして実感・体感できるからだ。これは非常に納得しやすい。だから、「表計算でシミュレーション」というお題では、「必要な道具をお金を出して手に入れる必要がない」「理解に必要な労力がさほど大きくない」という意味で、非常に「安い」。

　そして、次の「早い」である。これを言い換えてみると、「すぐにできる」ということだ。「表計算でシミュレーション」をする場合には、たとえば、時間的に変わらない（定常な）問題であれば、比較的簡単に計算シートを作ることができる。だから、すぐにできるようなシートを作ることができる範囲内では、「表計算でシミュレーション」というものはとても「早い」のである。ただ、あくまで「比較的簡単に計算シートを作ることができる範囲内では」ということが少し尾を引くのである。

　問題は、最後の「旨い」である。これは、多分、２つの意味がある。ひとつは単純に「実利的なメリット」だ。つまり、たとえば「すぐに仕事に使える」というようなことになる。そして、もう一つは「心としてのメリット」である。それは、たとえば「面白い」「意外だ」「へぇ～」といったような感覚を得ることだと思う。

　先の「比較的簡単に計算シートを作ることができる範囲内では」という先の制限は、これらふた種類の「旨い」と相反することが多い。それが、「表計算でシミュレーション」における吉野家のジレンマなのである。すぐに仕事で使うためには、「定量的に計算結果が正確である」ようなことが要求される。しかし、そうしようとすると、シートを作るのが面倒だったりして、「早い＝すぐにできる」ではなくなりがちになってしまう。
　また、「早い＝すぐにできる」ようなものは、比較的「当たり前」の計算結果が出てくる。たとえば、等方・等質的な空間でラプラス方程式で解いた静電界計算結果などは、「見た目にいかにも”自然”なもの」になる。それが”自然”なのだから、それでいいではないか、とも思う。しかし、その一方で、それでは意外性も何もなく、「へぇ～」「面白い」という感じを受けないのである。

　このように、「安い」「早い」「旨い」という吉野家提供の三つの評価軸から、「表計算でシミュレーション」を眺めてみると、「表計算でシミュレーションをする講習」が持ちがちな悩みが見えてくる。「早い」と「旨い」の兼ね合いの難しさが見えてくる。

　昨日の『エクセルでシミュレーション Vol.6 「夏にフライパンで卵焼き編」』の場合は、腕が良いシェフ（I講師）吉野家の法則の３評価項目を見事に上手く兼ね備えているのである。

この記事の「関連お勧め記事」を読む >>

キーワード(ブログ):吉野家の法則|吉野家のジレンマ|表計算|シミュレーション|表計算でシミュレーション|フライパン|卵焼き|ラプラス方程式|方程式|エクセルでシミュレーション|スプレッドシート|熱伝導|熱伝導方程式|体感|エクセル|道具|講習|お金|法則

2009-12-07[n年前へ]

■エクセルの計算ワークシートをRuby計算スクリプトに変換してみよう　

　下記で使ったエクセルファイルは、自己参照部分がなく、つまり反復計算が必要ないものを使ってしまいました。反復収束計算が必要なエクセルファイルを「続　エクセルの計算ワークシートをRubyでC言語に変換してみよう」でサーバ内に置きましたので、下記記事を読んだ後には、上記記事（さらにその後に続く記事など）を引き続きご覧ください。

　目的に対して達成方法があまりに過剰、あるいは、あまりに的外れで荒唐無稽なものというのは、それはそれで何だか面白いような気がします。

　今日は、そんなものを、ふと、けれど無性に作ってみたくなりました。

　先日、Microsoft Excelのような「表計算ソフト」スプレッドシートを使った「静電界計算や非定常熱伝導シミュレーション計算」をみっちりしてきました。離散化された物理式を表計算ソフトウェアを用いて計算を行うというのは、「セル」というメッシュと空間が感覚的に近く感じられることから、とても自然にシミュレーション計算を行う空間分割と計算領域との対応を感じることができるのが、とても便利で良いと思っています。

　もちろん、セル間の計算を「反復計算」を行うことで、複雑なことを気にせず、計算が自然に終わってしまう、というのも実に「自然」で「お手軽」で良い、と思っています。

　とはいえ、私はエクセルは苦手です。毎年何回か、エクセルでのシミュレーション計算を（悩んでいる）人に教えるという作業をするのですが、それでもエクセルを使うのは苦手です。そこで、エクセルで作った離散化シミュレーション用.xlsシートをRuby Script（プログラム）に自動的に変換する、Rubyスクリプトを作ってみることにしました。そう、「エクセルで物理シミュレーションを学んだ人が、そのエクセルシートをそのまま多言語に移植することができる」スクリプトを作ってみよう、と考えてみたのです。

　作ったコードxls2rb.rbは次のようになります（近日中にサーバに置いて置きます）。これは、「反復計算を使った」エクセルファイルを読み込み、それをRubyスクリプトに変換するスクリプトです。「表計算ソフト」スプレッドシートを使いった「静電界計算や非定常熱伝導シミュレーション計算」は、四則演算と周囲の空間が持つ値の計算だけで行うことができます。だから、そういう「条件」下では、そんなスクリプトを作るのも比較的簡単です。初期化や反復計算をそれぞれ「関数」化しているとはいえ、変数はすべてグローバル変数ですし、そこら辺の「エクセル感」も再現してみたスクリプトです。

require 'win32ole'

def getAbsolutePath(filename)
  fso=WIN32OLE.new('Scripting.FileSystemObject')
  fso.GetAbsolutePathName(filename)
end

def getAlphabet(n)
  val=n.to_f/25.0 
  mod=n%25
  result=''
  result+=('a'..'z').to_a[(n-val)/25] if val>1
  result+=('a'..'z').to_a[mod]
end

def defFunc(state,book)
  src=''
  book.Worksheets.each do |sheet|
    y=1
    sheet.UsedRange.Rows.each do |row|
      x=0
      record=[]
      row.Columns.each do |cell|
        if state==:init &&cell.Value!=''
          record＜＜'  '+'$'+getAlphabet(x)+y.to_s+
            '='+cell.Value.to_s if cell.Value.to_s!=''
        end
        if state==:calc &&cell.Formula!=''
          t=cell.Formula.sub(/[=$]/,'')
          t=t.downcase.gsub(/([a-zA-Z]+\d+)/,'$\1')
          record＜＜'  '+'$'+getAlphabet(x)+y.to_s+'='+t
        end
        x+=1
      end
      src+=record.join("\n")+"\n" if record.join('').gsub("\n",'')!=''
      y+=1
    end
  end
  return src
end

filename=getAbsolutePath(ARGV[0])
excel=WIN32OLE.new('Excel.Application')
book=excel.Workbooks.Open(filename)
initsrc=defFunc(:init,book)
calcsrc=defFunc(:calc,book)
book.close
excel.quit
GC.start

puts ＜＜INIT
# autocreated ruby script from excel file
# jun hirabayashi jun@irax.net http://www.hirax.net

def init
#{initsrc}end

def calc
#{calcsrc}end

10.times do
  calc
end
INIT

　ちなみに、このスクリプトを

ruby xls2rb.rb ex.xls

という具合にして（引数は変換したいXLSファイルです）、実行すると、次のようなスクリプトができあがります。ちなみに、ここで使ったex.xlsファイルは、ラプラス方程式を3X3のセルに離散化し解く、実に単純なエクセルシートです。（この辺りのファイル一式を週末にでもサーバ上に置いておきます）

# autocreated ruby script from excel file
# jun hirabayashi jun@irax.net http://www.hirax.net

def init
  $a1=1.0
  $b1=2.0
  $c1=3.0
  $a2=1.0
  $b2=2.0
  $c2=5.0
  $a3=1.0
  $b3=2.0
  $c3=3.0
end

def calc
  $a1=1
  $b1=2
  $c1=3
  $a2=1
  $b2=2
  $c2=$b2+$c1
  $a3=1
  $b3=2
  $c3=3
end

10.times do
  calc
end

　つまり、今日私が作ったスクリプトの動作は、エクセルが最初に行う初期化ルーチンを"init"関数として定義（作成）し、次に行う反復計算を"calc"関数として定義（作成）し、それを（適当に決めた）10回繰り返すスクリプトを作り出す、という具合です。ポイントは初期化時には、cell.Valueを用いることで初期数値を設定し、逐次計算時にはcell.Formulaを使うことで数式を使う、という「使い分け」になります。反復計算自体は、ガウスザイデル法によって行われます。

　あとは適当に、知りたい値を出力する（たとえば、"puts $c2"といった）出力処理文でも書き足せば、はい、シミュレーション・rubyプログラムのできあがり、というわけです。

離散化された物理計算をするために作成したエクセル・シートを、Rubyスクリプトに自動で変換し、好きに加工できるプログラム…って便利なような、そもそもそんな用途ってある訳ないような…というのが正直で的確な感想だと思います。つまり、それはかなり無意味なツールです。

　他の言語に置き換えて、高速化指向の変換プログラムを書いてみるのも（一回くらいはやってみようと思いますが、今ひとつ「魅力」に欠けるように思います。

　今日作った、「離散化された物理現象を計算するために作成したエクセル・シートを、Rubyスクリプトに自動で変換するプログラム」なんていうものを、（何だか馬鹿馬鹿しいけれど）意外に少し面白い笑える、そう思える人が一人でもいたら、幸いに思います。

この記事の「関連お勧め記事」を読む >>

2009-12-19[n年前へ]

■名前付きセルのあるエクセルのワークシートをC++言語プログラムに変換してみよう　

これまで「続　エクセルの計算ワークシートをRubyでC言語に変換してみよう」や「エクセルの計算ワークシートをRuby計算スクリプトに変換してみよう」で、エクセルの表計算シートを他の言語のプログラムに変換する、なんていうことをしてきました。ここで想定している「エクセルの表計算シート」というのは、「エクセルで作った離散化シミュレーション用.xlsシート」を主眼に置いています。つまり、何らかの方程式を差分化し、エクセルシート上でその差分化された空間を表現し、反復収束計算ことで求めたい結果を得る、そんなためのエクセルシートを主眼に置いています。

　ところで、そんな風にエクセルシートを使うときには、セルに名前をつけたくなります。たとえば、真空の透磁率をA1セルに入れたら、そのセルを"A1"セルでなく、"eps"なんていう名前で参照したくなります。そこで、たとえばこんな風にセルに名前をつけます。すると、そのセルの値を、"A1"というようにも参照できるのに加えて、"eps"なんていう名前でもアクセスすることができるようになります。そうすれば、他のセルでは"=eps*4"なんていう風に数式を入力することができるわけです(参考ビデオ）。

　そこで、今回は名前付きセルを使ったエクセルのワークシート（簡単のために、一枚目のシートだけを使ったエクセルブックを前提にしています）をC++言語プログラムに変換するRubyスクリプトを書いてみました。変換用のRubyスクリプトや、名前付きセルを使った（ラプラス方程式を解く）エクセルシートや、エクセルシートから変換・作成されたC++言語ソースファイルは、ここに置いておきました。このサンプルのエクセルファイルでは、中心のセルの値を変化させるために入れるセルに"centerVal"という名前を付けています。そのため、変換されたC++ソースには、

  C3=centerVal;

といった記述が現われています。エクセルでは、「名前」はセルにではなくブックの直下で管理されているので、Ruby変換スクリプトでは、

names={}
book.names.each do |name|
  cell=$1.gsub('$','') if /!([^!]+)$/=~name.RefersTo
  names[cell]=name.name
end

といったようなコードにしてあります。

　名前付きセルを使ったエクセルシートを使い物理定数や中間変数などをわかりやすく表現した上で、離散化シミュレーションをシート上の「いかにもわかりやすく「差分化された空間で」実感した後に、（その自分自身が作ったスプレッド・シートを元に）変数の名前が（少なくともA1とかD4とかいう名前よりは）わかりやすいシミュレーションプログラムが自動生成されるとしたら、つまり、自分自身がスプレッド・シート上で作ったものが、C++言語の（もちろん他の言語でも）プログラム・ソースとして眺めることができるとしたら、…これって結構面白いと思いません？

この記事の「関連お勧め記事」を読む >>

2012-07-02[n年前へ]

■ポアソン方程式は「ふたつの胸の膨らみ」で、ラプラス方程式は「胸の谷間の曲面」だ!?　

　真空中に円板（平坦）状の電荷分布が離れて「ふたつ」あった場合の電位分布、それをポアソン（ラプラス）方程式を解いてグラフにしてみました。円板状といっても、つまりはとても「平坦」な電荷分布が作り出す電位分布は、実に魅力的な曲面です。下に貼り付けた曲面グラフは、小さな平円板状電荷が離れてあった場合の電位分布を計算してみた結果です。

　ラプラス作用素 ∇・（∇）は、この曲面でこそ、一番わかりやすく実感できます。ラプラス作用素がゼロでない値になるという「ポワソン方程式」は、「平面を押し上げるふたつの胸の膨らみ」で「ラプラス作用素がゼロでない＝盛り上がっていること（あるいは堀りえぐれていること）」実感することができます。…そして、ラプラス作用素がゼロになるというラプラス方程式は、「胸の谷間の”馬の鞍”状の双曲面」のように、ある軸に曲がりがあったとしたら・（その軸の曲がりを生むように）その他の軸は逆の向きに曲がっているという状態を実感できるはずなのです。