2012-09-12[n年前へ]
■「Cカップのバストなんて実在するわけがない！」ことの数学的証明 
「真面目に考えてみると、意外に難しくて、意外に面白い」ということがあるものです。たとえ「真面目に考えてみる対象」が「どんなこと」であっても、です。
ブラジャーのカップサイズは、アンダーバストとトップバストの「差」で決まります。「おっぱい解析向けライブラリを書いてみる!? 第1回」で書いた（コーディングした）ような具合で、たとえば、アンダーバストとトップバストの差が5cmならAAAカップ、7.5cmならAAカップ、10cmならAカップ…15cmならCカップ、という具合です。
とても単純に、胸回りの胴体に「球状のバスト」が付いているとすると、カップサイズ＝トップバストとアンダーバストの差は「円弧と弦の長さの差分を求めよ」という問題に置き換えることができます。…たとえば、Aカップなら、胸のバストカップ断面に相当する長さ（弦）に１０ｃｍ足した円弧の形状が、それすなわちAカップのバスト形状だ、という具合です。
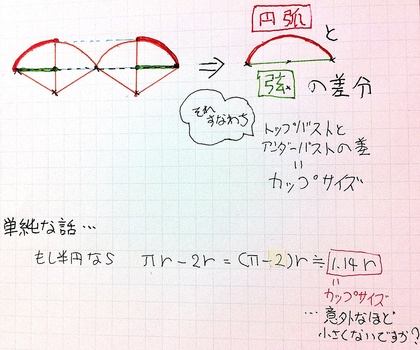
この「円弧と弦の長さの差分を求めよ」問題は、実は意外に難しい問題です。そこで、わかりやすく「もしも、胸が半球形状だったなら」という風に考えてみることにします。つまり、もしも「世界が１００人の村だったら」という風に単純化してみるのです。
もちろん、半球状バストなんて、そんなマルマルとした超立体的バストなんか非現実的ですが、そんな非現実的な立体バストの場合、「円弧と弦の長さの差分＝トップバストとアンダーバストの差＝カップサイズ」は「（パイ−２）×胸の半径」になります。パイ＝円周率は3.14...ですから、「胸の半径に約1.14を掛けたもの」が「トップバストとアンダーバストの差＝カップサイズ」に相当するわけです。
自分の胸に手を当てて、じっと考えてみて下さい。あなたの「片胸の幅はせいぜい１５ｃｍくらい」ではないでしょうか。ということは、その片胸に半球状バストが張り付いているとすると、その半球状バストの半径は「１５ｃｍのさらに半分＝7.5ｃｍほど」になります。その7.5cmに1.14を掛けた結果の8.6cm が「トップバストとアンダーバストの差＝カップサイズ」で、（トップバストとアンダーバストの差が）7.5cmならAAカップ・10cmならAカップということを思い出せば、（いくらなんでも、それはありえなさそうな）半球状のマルっと超立体な３Dバストですら、カップサイズは（せいぜい）Aカップに過ぎない…ということになるのです。
超非現実的でありえない「半球状のマルっと超立体な３Dバストでも、Aカップに過ぎない」となると、「アンダーバストとトップバストの差が15cmのCカップ」なんて、そんな物体が果たしてこの世に実在するものでしょうか？バストのカップサイズについて「真面目に考えてみる」と、「そんなもの、Cカップなんてものはありえない・実在するわけがない」…と気づかされるのではないでしょうか。
…といったことを「実感」するために書いた検証用「体感コード」を動かしてみたのが、下の動画になります。（アンダーでなく）トップバスト数値と「カップ」の組み合わせでバスト形状を眺めてみるのも面白い、かもしれませんね。（また、この3次元版が「バストとカップサイズからグリグリ・マルマルな立体３Dを眺めてみよう!?」になります）
2014-04-20[n年前へ]
■円周率（パイ）なんて簡単にわかるさ。「そう、指１本とおっぱいがあればね！」
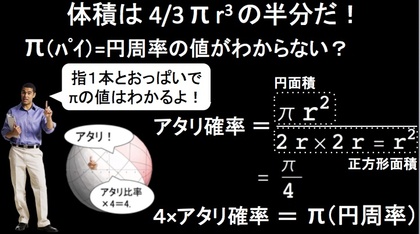フォン・ノイマンが名付け親だというモンテカルロ法の説明のために、エクセルで円周率を計算するモンテカルロ法シートを適当に作り、こんな「スライド」を描いてみました。ちなみに、そのエクセルシートを動かしてみたようすが、その下に貼り付けた動画です。
円周率（パイ）の値なんて簡単にわかるさ。
「そう、指１本とおっぱいがあればね！」
ちなみに、下のエクセル動画は、「反復計算」と「図形選択で数式記入部に”＝セル番号”を入れると、図形テキストを任意に変更できる、という仕組みを使っています。
2014-04-27[n年前へ]
■世界で一番簡単な円周率の求め方
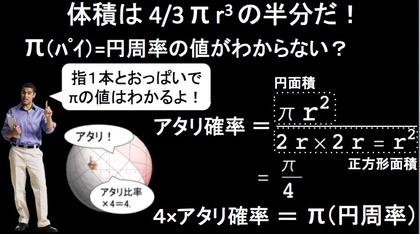円周率π（パイ）の値を知りたい時、あなたなら一体どうするでしょうか？ …というわけで、世界で一番簡単な円周率の求め方（モンテカルロシミュレーションとか、ニュートン力学とか、弾性体力学とか流体力学とか…）を動画にしてみました。
円周率(π=ﾊﾟｲ）なんて簡単にわかるさ！
そう、指１本とおっぱいがあればね。
2015-07-05[n年前へ]
■「１４４層のパイ生地」と「誤用としての冪乗」
薄く重なったパイ生地が「１４４層」という数字を聴いて頭の中に「？」マークが浮かんだけれど、なるほど全部で「4つ折りx3つ折りx4つ折りx3つ折り=144層」なのか！
クロワッサン、デニッシュ、ブリオッシュは「ペイストリー」に分類されますが、“THE PIE & PASTRY BIBLE”によると、その共通点や違いは以下のようになります。
層の多さは折りパイ、クロワッサン、デニッシュの順。イースト使用の生地は二次発酵させる為に暖かい場所に置く必要があり、折り込みの回数が多いと生地が耐えられない。
・折り込み回数（層の数）は、折りパイ生地：6回以上（729）、クロワッサン：4回（81）、デニッシュ：3回（27）
・折り込みの回数に耐える為、折りパイ生地はグルテンのしっかりした強い生地を作る必要があり、グルテン含有率の高い粉を使ったり、生地をよく捏ねたりする。また、バターが溶け出さないように、焼くまで生地を冷やしておく必要がある。
・デニッシュは生地に卵を含み、折り込みの回数もクロワッサンより一つ少なく、焼き上がりはクロワッサンよりもフレーキーな感じではないが、ふんわりとして柔らかい。
デニッシュの定義って？
関係無いけど、これも面白い。
"元来は、単に「冪（べき）」と表現した。「冪乗（べきじょう）」という語は、誤用が定着したものである。 「冪」の文字はもともと「覆う、覆うもの」という意味の漢字であり、江戸時代の和算家は略字として「巾」を用いていた。ところがどちらも常用漢字・当用漢字に含まれなかったことから1950年代以降、出版物などでは仮名書きまたは「累乗」への書き換えが進められ、結果として初等数学の教科書ではもっぱら「累乗」が用いられた。この際、n 乗を取る操作の伝統的名称である「n 乗冪」 と「累乗」が混同され、「冪乗（べきじょう）」という語を生じた。"
」など。