hirax.net::Keywords::「円周率」のブログ

■「Cカップのバストなんて実在するわけがない！」ことの数学的証明　

　「真面目に考えてみると、意外に難しくて、意外に面白い」ということがあるものです。たとえ「真面目に考えてみる対象」が「どんなこと」であっても、です。

　ブラジャーのカップサイズは、アンダーバストとトップバストの「差」で決まります。「おっぱい解析向けライブラリを書いてみる!? 第1回」で書いた（コーディングした）ような具合で、たとえば、アンダーバストとトップバストの差が5cmならAAAカップ、7.5cmならAAカップ、10cmならAカップ…15cmならCカップ、という具合です。

　とても単純に、胸回りの胴体に「球状のバスト」が付いているとすると、カップサイズ＝トップバストとアンダーバストの差は「円弧と弦の長さの差分を求めよ」という問題に置き換えることができます。…たとえば、Aカップなら、胸のバストカップ断面に相当する長さ（弦）に１０ｃｍ足した円弧の形状が、それすなわちAカップのバスト形状だ、という具合です。

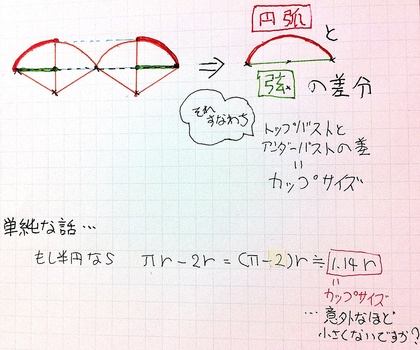
　この「円弧と弦の長さの差分を求めよ」問題は、実は意外に難しい問題です。そこで、わかりやすく「もしも、胸が半球形状だったなら」という風に考えてみることにします。つまり、もしも「世界が１００人の村だったら」という風に単純化してみるのです。

　もちろん、半球状バストなんて、そんなマルマルとした超立体的バストなんか非現実的ですが、そんな非現実的な立体バストの場合、「円弧と弦の長さの差分＝トップバストとアンダーバストの差＝カップサイズ」は「（パイ−２）×胸の半径」になります。パイ＝円周率は3.14...ですから、「胸の半径に約1.14を掛けたもの」が「トップバストとアンダーバストの差＝カップサイズ」に相当するわけです。

　自分の胸に手を当てて、じっと考えてみて下さい。あなたの「片胸の幅はせいぜい１５ｃｍくらい」ではないでしょうか。ということは、その片胸に半球状バストが張り付いているとすると、その半球状バストの半径は「１５ｃｍのさらに半分＝7.5ｃｍほど」になります。その7.5cmに1.14を掛けた結果の8.6cm が「トップバストとアンダーバストの差＝カップサイズ」で、（トップバストとアンダーバストの差が）7.5cmならAAカップ・10cmならAカップということを思い出せば、（いくらなんでも、それはありえなさそうな）半球状のマルっと超立体な３Dバストですら、カップサイズは（せいぜい）Aカップに過ぎない…ということになるのです。

　超非現実的でありえない「半球状のマルっと超立体な３Dバストでも、Aカップに過ぎない」となると、「アンダーバストとトップバストの差が15cmのCカップ」なんて、そんな物体が果たしてこの世に実在するものでしょうか？バストのカップサイズについて「真面目に考えてみる」と、「そんなもの、Cカップなんてものはありえない・実在するわけがない」…と気づかされるのではないでしょうか。

■円周率（パイ）なんて簡単にわかるさ。「そう、指１本とおっぱいがあればね！」　

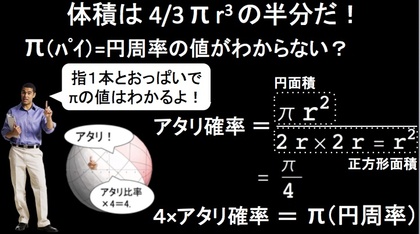　フォン・ノイマンが名付け親だというモンテカルロ法の説明のために、エクセルで円周率を計算するモンテカルロ法シートを適当に作り、こんな「スライド」を描いてみました。ちなみに、そのエクセルシートを動かしてみたようすが、その下に貼り付けた動画です。

　円周率（パイ）の値なんて簡単にわかるさ。
「そう、指１本とおっぱいがあればね！」

　ちなみに、下のエクセル動画は、「反復計算」と「図形選択で数式記入部に”＝セル番号”を入れると、図形テキストを任意に変更できる、という仕組みを使っています。

■世界で一番簡単な円周率の求め方　

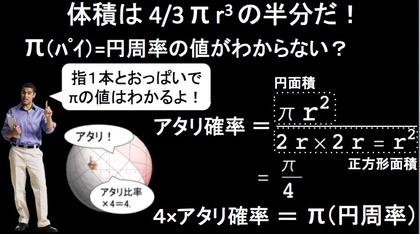　円周率π（パイ）の値を知りたい時、あなたなら一体どうするでしょうか？　…というわけで、世界で一番簡単な円周率の求め方（モンテカルロシミュレーションとか、ニュートン力学とか、弾性体力学とか流体力学とか…）を動画にしてみました。

円周率(π=ﾊﾟｲ）なんて簡単にわかるさ！

そう、指１本とおっぱいがあればね。

■手回し計算器でGoogleと大決闘！目指せ円周率……全3桁　

　「ソフトウェアデザイン 2019年10月」に『手回し計算器でGoogleと大決闘！目指せ円周率……全3桁』を書きました。円周率をウォリス（Wallis）の公式を使って、手回し計算器の（履歴保持機能を使い）乗算積で計算していく話です。

　そしてまた、手回し計算器が使われていた'50年代の話だけでなく、その後後の'70〜'80、そして、'90移行の今にいたる計算器の話です。