2009-06-24[n年前へ]
■Mathematicaで発色シミュレーションをオブジェクト風記述にする 
Mathematicaで発色シミュレーションをモンテカルロ法で行うライブラリを作りました。オブジェクト風記述にできるのが特徴です。（今週末まで修正作業を行うつもりなので、多少、仕様は変わるかもしれませんが）たとえば、
Light[new][in,Layer[new]][showTrace]という記述をすると、下のグラフのような、三次元構造の中で反射・屈折・散乱を行う「光」のスペクトルが、どのように変化していったかを知ることができます。
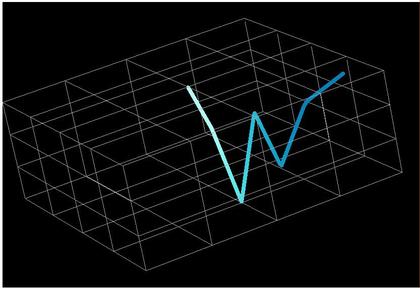
この例の場合は、Layer[new]で、デフォルトのコンストラクタで作成された水色の層に入射した光の挙動を眺めてみたものになります。層内で多重反射した後に、水色に染まって層の外へ出て行ったことがわかる、という例になります。
ライブラリは、週末にサイト上へアップロードする予定です。
2009-07-03[n年前へ]
■例題・説明文付き色処理・シミュレーションMathematicaライブラリ
Mathematicaで作った色処理関連の関数群・それらを使いさらにオブジェクト指向に書いた（モンテカルロ光伝播シミュレーション機能付き）クラス群のライブラリに例題や説明文を付けたものを作りました。そのライブラリを記述したノートブックを、ColorLib_amature_on_7.0_1.01.nb (5.6MB) として、サイト上に置いておきます。
Mathematicaを持っていない方でも、Mathematica Playerを使えば、Mathematicaのノートブックを眺めることができます。ですから、もしも題材に興味がある方ならば、「なるほど、この処理はこんな風に書いているのか」「ここはこう直した方が良いんじゃないのか」など、きっとそれなりに楽しむことができると思います。
たとえば、Mathematicaで書いたライブラリを他の言語で書き直そうとしたときに、書きにくいと感じる部分こそが、Mathematica「らしい」だろうと思います。もちろん、これはMathematicaに限らない、プログラム言語にも限らない「個性」ということに関する一般的な話です。
2013-06-01[n年前へ]
■「麻雀の山とツモに関する確率シミュレート」
…しかし、場に一枚見えている両面待ちが、山にどれだけ残っていて、どれだけの確率でツモれるかって、意外と感覚じゃ分からない。ということで、シミュレータを作りました。
「７巡目で両面聴牌、場に当たり牌は１枚しか見えていない。ツモれる確率は？」
中張牌の待ちとして他家が河に捨てる確率を25%と見積もると、山に残る枚数は3.88枚と出ます。これをツモの確率に入れると、55%でツモれることが分かります。
2014-04-20[n年前へ]
■円周率（パイ）なんて簡単にわかるさ。「そう、指１本とおっぱいがあればね！」
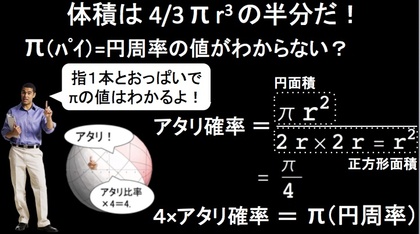フォン・ノイマンが名付け親だというモンテカルロ法の説明のために、エクセルで円周率を計算するモンテカルロ法シートを適当に作り、こんな「スライド」を描いてみました。ちなみに、そのエクセルシートを動かしてみたようすが、その下に貼り付けた動画です。
円周率（パイ）の値なんて簡単にわかるさ。
「そう、指１本とおっぱいがあればね！」
ちなみに、下のエクセル動画は、「反復計算」と「図形選択で数式記入部に”＝セル番号”を入れると、図形テキストを任意に変更できる、という仕組みを使っています。
」など。