2002-02-20[n年前へ]
■「やおい」の評価演算子 
ベクトルの彼方で待ってて II
東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか？
「福田Ｘ小泉っていうのは、結構上手くやっているのかな？」と私が言うと、おもむろに
「あれは、福田Ｘ小泉じゃなくて、絶対あれは小泉Ｘ福田なのー」とその記者が言ったのである。何を言っているのかその意味がよく判らないまま、「ん〜？」と私が首を傾げていると、繰り返し
「福田Ｘ小泉と小泉Ｘ福田は全然意味が違うのー」と言い始めるのである。何が何だか訳がわからない。じゃぁ、何か？小泉Ｘ福田だと小泉純一郎が総理大臣で福田康夫が官房長官だけど、福田Ｘ小泉だと福田康夫が総理大臣で小泉純一郎が官房長官になるとでも言うのか？？政治の世界では、言う順番で総理大臣が決まるとでも言うのか？と私が口をはさむと、
「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」と言うのだ。なんだコイツ？政界は判るけど、やおい界って一体何処の世界の話だ？？と、困惑する私も構わず、そこから延々と長い演説が始まった…。その大河ドラマのようにやたらと長い話を要約すると、
- やおい → 一部の女性が好む「男性同士の恋愛もののストーリー」のこと
- Ｘ → やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…
で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。 今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。
で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
まずは、色々な人物（実際の人物であったり、小説などの登場人物であったり）のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を
- 攻めベクトル
- 受けベクトル
 |
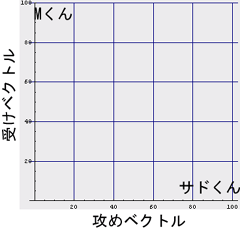そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、
カップリング適性ベクトル = （攻め度(s)、受け度(m)）と表記して、例えばAさんのカップリング適性ベクトルを(As, Am)と表すことにしてみよう。すると、Aさんが「攻め」でBさんが「受け」のカップリング適性は、この二人の適性ベクトルのベクトル積として表すことができる。つまり、
A×Bのカップリング適性 = ( As * Bm - Am * Bs )となるわけである。式を眺めれば判るように、Aさんの攻め度が高くて、Bさんの受け度が高ければ、この評価関数は高い値を返す。つまり、「A×Bの順序は正しいのだー」という評価を返す。つまり、「A×B」はなかなか良いカップルだー、と教えてくれる。また、もしAさんの受け度が高くて、Bさんの攻め度が高ければ、低い値を返す。つまり、「A×Bの順序は絶対間違ってるのだー」と評価してくれるのである。なんともありがたいことに（いや別にありがたくはないか…）、この「やおいのカップリング評価演算子」が「福田Ｘ小泉」と「小泉Ｘ福田」のどちらが自然なのかを教えてくれるのだ。試しに、上のサドくんとMくんであれば、「サドくん×Mくん」= (100,0)×(0,100) = 100*100 - 0*0 = 10000でとっても「良い感じ」でああるが、「Mくん×サドくん」= (0,100)×(100,0) = 0*0 - 100*100 = -10000で「このカップリングは絶対順序が違うー」と判るわけである。
= Aさんの攻め度 * Bさんの受け度
- Aさんの受け度 * Bさんの攻め度
とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか（?）「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。
ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。
これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。
一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。
「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
「愛はどんな形をしているか知っているか？」「見た事ないからわかりません。」「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう？... 異性愛か、同性愛か、そんなものじゃない …たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2008-05-02[n年前へ]
■理科の教科書に出てくる「仕事」と「駅前で聴く音楽」
力積で考える「カミソリパンチ」と「ググゥーッと押し込む打撃」の「力積」は「力の大きさと力が働く時間を掛けあわせたもの」です。その一方、「力と変位を掛け合わせた（内積）もの」を、理科の教科書の中では「仕事」と呼びます。
中学か高校の頃、理科か物理の教科書の中で「仕事」という言葉が出てきたときに、何だかその言葉の感覚と教科書の中での定義がズレていて首を捻ったような覚えがあります。たとえば、Wikipedia に「仕事とは呼ばない例」として挙げられているようなこと
人が重い荷物を抱え・支えている状況では、荷物は静止していて、エネルギーは変わらない。つまり、この場合、人は荷物に対して仕事をしていない。を聞きながら、それは仕事でないのかぁ……!?と悩んだわけです。「重い荷物を抱え・支えている状況」はとてもしんどそうなのになぁ……と感じました。それは「仕事」ではないかもしれないけれど、筋肉がパンパンにつく肉体改造・大成長状態だろうに……と思ったのです。
私と同じように、理科の教科書を読みながら、頭の中に大きなハテナマークを浮かべた人はきっと多いと思います。
先日、「手作り三次元グラフ」と"Life Work"や「"複雑極まりない"複素平面」上に「仕事」と「趣味」を描くといったラクガキをしました。そのとき、”理科の教科書の中の「仕事」の説明を読みながら、頭に浮かんだハテナマーク”を思い出しました。
あのラクガキ中の「他人の満足」という軸は、「その人がどれだけ他の人を満足させたか・その人の力で他の人（の心を）どれだけ動かしたか」という、まるで理科の教科書に出てくる「仕事」なのかもしれない、と感じたのでした。
駅前で誰かが演奏している音楽を聴いて心が動かされたとき、「何だか心の中に豊かなエネルギーが入ってきたなぁ」と思ったりもします。それを、理科の教科書を思い出しながら言うならば、「あぁ誰かに仕事をされたんだなぁ」と感じたりするのです。
「力積」と「仕事」はイコールではありません。もしも、「自らを脅かし・揺るがし、新たな出会いや発見がある」としたら、それは「仕事」よりは、力積に近いものなのだろうか、と思っています。
」など。