hirax.net::Keywords::「平方根」のブログ

■君の歌は僕の歌　

竹内まりやの「平方根」

　半年ほど前、TBSのテレビ番組「USO」で放映されていた「竹内まりやの歌の音程を下げると山下達郎の歌に聞こえる」という話を観た。なんでも、その話は「ネット上をにぎわしている情報」ということだったのだけれども、ワタシには全然知らない話題だった。だから、その放映されていた「音程を下げた竹内まりやの歌」を聴いて、とてもびっくりした。確かに「山下達郎の歌」に聞こえるのである。そして、それにビックリすると同時にとても新鮮に面白く感じたのだった。

　山下達郎はワタシも好きだったりするし、しかも山下達郎は決して多作というわけではないので、「山下達郎が他人の曲をカバーをする新たな音源」をワタシが勝手に増やせるというのはとても魅力的である。そこで、ワタシは再生スピードを変えずに音程だけを変えることができるWinAmp　+　Pacemakerを使って、竹内まりやの「元気を出して」の音程を下げて、ワタシも山下達郎版「元気を出して」を作ってみることにした。それが下の二つのファイル、「元気を出して」の最後の部分の「オリジナル」と「音程を下げたもの」である。

• 竹内まりや　「元気を出して（オリジナル）」
• 竹内まりや　「元気を出して（音程を下げたもの）＝山下達郎風」

これを聴くと、確かに山下達郎が竹内まりやの「元気を出して」を歌っているかのように聞こえるから不思議だ。単にそう耳に聞こえるだけではなくて、山下達郎が歌っている様子、そして山下達郎が竹内まりやに「君の歌は僕の歌」だよ、という気持ちを込めて歌っている様子すらワタシの頭の中に浮かぶのである。
 

　そこで、次に調子に乗って今度は鬼束ちひろの「流星群」の音程を下げてみた。今度は山下達郎が歌う「流星群」が手に入れよう、と思ったわけだ。ワタシの手持ちの音源全曲に対して山下達郎化計画を発動しようとしたのである。科学、いや単に"WinAmp+ Pacemaker"の力で山下達郎多作化計画を発動しようとしたわけだ。
　　ところが、である。なんと「流星群」を歌っている歌手は今回は山下達郎には聞こえなかったのである。、そこには「流星群」をしみじみと歌いあげている平井堅がいたのだった。切々と「流星群」を歌い上げる平井堅の実に濃い顔がワタシの頭の中に確かに浮かんでしまうのだった。

• 鬼束ちひろ　「流星群（オリジナル）」
• 鬼束ちひろ　「流星群（音程を下げたもの）＝平井堅風」

何故、竹内まりやの歌の音程を下げると山下達郎になって、鬼束ちひろの歌の音程を下げると平井堅になるのだろう？竹内まりやと山下達郎が夫婦だからだろうか。…いやいや、そんな説明はあまりに精神論的すぎる。そんな説明をしたら、絶対バカにされるに決まってる。それになにより、鬼束ちひろと平井堅は夫婦ではない。きっと、何か他の確かな理由がきっとどこかに隠れているハズである。
 

　そこで、「竹内まりや、山下達郎、鬼束ちひろ、山下達郎」の歌を周波数を時系列的に眺めるスペクトログラムで比較・分析してみることにした。といっても、竹内まりやと山下達郎が「同じ言葉で歌っていて、なおかつ（本人の声以外の）バックミュージックが無いような音源」を手に入れるのが少し面倒だったので、今回は「声質」などを考察することはあきらめ、とりあえずはそれぞれの歌手の「歌い方」に注目してみることにした。
 

　まずは、竹内まりやの「元気を出して」と山下達郎の"So Much In Love"をスペクトログラムで眺めてみる。縦軸が周波数軸で、上に行くほど高い周波数の声である。当然、下に行くほど低い声である。そして、横軸は時間軸で、左の方が時間的に先で、右の方が時間的に後になっている。結局、このスペクトログラムの中にはさまざまな倍音が白い線となって描かれているのである。
 

「竹内まりや」と「山下達郎」の歌い方のスペクトログラムでの比較

竹内まりや　「元気を出して」

山下達郎　"So Much In Love"

　まず、このスペクトログラムを眺めていると、竹内まりやも山下達郎も「ほんの少しだけ不規則なビブラート」がとても多いことがわかる。歌のかなりの部分にビブラートがかかっていて、竹内まりやの歌のやわらかさを支えている（少なくともワタシにはそう聞こえる）。そして、それは山下達郎とも共通している特徴である。

　また、それぞれのスペクトログラムの音の出し始め部をよく眺めてみるとちょうど「√」の形をした部分が数多く見られることに気づく。上に示した、竹内まりやの「元気を出して」のスペクトログラム中で青い矩形で囲った部分を見れば、そんな「√」形の部分があることが判るだろう。この「√（ルート）」形状は、「音の高さが連続的に変化している（一種のポルタメントのように）」ことを示しているわけだけれど、そんな√形状が竹内まりやと山下達郎の局の中に多いことが特に判りやすい部分を示したのが下のスペクトログラムだ。二人の歌の中にとてもよく似た√（root）マークがある（そして実はそれがとても数多くある）ことが判ると思う。
 

竹内まりやと山下達郎に共通する√ （root）

竹内まりや　「元気を出して」

山下達郎　「君の瞳に恋してる」

　こうしてスペクトログラムを眺めてみると、竹内まりやと山下達郎の二人ともに、「ある音程の音を出すために、

1. まず目的の音程よりも低いところから声を出し始め、
2. しかも最初の一瞬は逆にほんのちょっとだけ下げて、
3. と思ったら目的の音まで一直線に音程を上げて、
4. そして、一定の音程をキープする

という歌い方」が共通していることが判ると思う。竹内まりやの歌にあふれるルーツ（√）は山下達郎の歌の中にあるルーツ（√）に繋がっていたのである。文字通り、竹内まりやのルーツは山下達郎のルーツだったのである。その歌の源は二人ともに同じものだったわけなのである。と、書いてる内に、とても非科学的になってしまったような気がしてきたので、ここで超強引に科学的に書いてしまえば、ここに

という方程式が実は成り立っていて、この「竹内まりや・山下達郎」方程式を解くことで、当然のごとく

竹内まりや＝山下達郎

という答えが得られるわけなのである。つまり、竹内まりやの歌の音程を下げると山下達郎になると、この方程式から証明されるわけなのである。実に科学的な説明ではないだろうか……。
 
 
 

　…それはさておき、鬼束ちひろと平井堅の場合は一体どうなのだろうか。歌の中で声にかけられるビブラートは「竹内まりやと山下達郎」とどう違うのだろうか、そしてまた声（ある音程の声）の出し始めの様子はどのようになっているだろうか？というわけで、次に鬼束ちひろの「流星群」と平井堅の「大きな古時計」のスペクトログラムを眺めてみる。
 

「鬼束ちひろ」と「平井堅」の歌い方のスペクトログラムでの比較

鬼束ちひろ　「流星群」

平井堅　「大きな古時計」

　
　こうしてみると、もちろん鬼束ちひろや平井堅だって歌にビブラートをかけてはいる。しかし、先ほどの竹内まりやと山下達郎の場合と比べると、まるで人工的と言っても良いほどに規則正しいビブラートがかかっていることが判ると思う。また、ビブラートをかけていない部分では、実に一定な音程をキープしていることが判る。しかも、それぞれの音程で声を出し始める最初の部分では、その音程にいきなり「すっと入っている」のである。竹内まりやと山下達郎が「√」形状の声の出し方であるならば、鬼束ちひろと平井堅の場合は「電気回路の抵抗記号」のような声の出し方をするのである。そんな共通点がこの二人の間にはあったのである。鬼束ちひろの歌い方と平井堅の歌い方は実によく似ていたのである。だから、鬼束ちひろの歌の音程を下げると平井堅に聞こえたのかもしれない。誰でもカラオケに行って色んな歌手の歌を歌う機会があるだろうけれど、こんな風にスペクトログラム上のそれぞれの歌手の歌い方の特徴を意識しながら歌えば、もしかしたら面白いことだろう。誰もが平井堅や竹内まりやになりきれるかもしれない。
 

　ところで、最近のカラオケはとっても賢いリモコンがついていて、「＊＊年に流れていた曲」というような検索ができる。すると、同年代の人とカラオケに行くとその年代に共通する「あの頃の曲」をかけまくって、歌いまくることになる。自分たちだけに判る懐メロ、だけどそこにいる人達にとっては「懐メロ」ではなくて今でも生き生きとしている曲、が次々とかけられることになる。中学時代、高校時代、ずっと昔のあの頃に流れていたヒットソング、そこにいる人に共通するルーツの曲のオンパレードになる。そんな時には、誰かが入れた歌全てがいつの間にか全員の合唱に変わっていたりする。

　同年代の人とカラオケは（特にそんなリモコンを使うときには）、まさに「他の人が歌う歌全てが自分の歌」、つまりは「君の歌は僕の歌」になる。、「元気を出して（オリジナル）」の最後の部分、竹内まりやの声を中央に、右から山下達郎の声が、左から薬師丸ひろ子の声が流れ溶け合っているのを聴きながら、そんな景色をを思い浮かべてみるのもきっと面白いんじゃないかと思う。

■品川から三島までの揺れデータ　

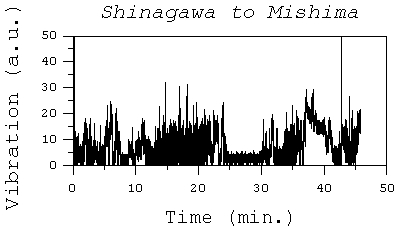
　というわけで、下りのこだま585号 8号車 通路側のシート上の「品川駅から三島駅まで」の揺れデータ(10ms間隔)です。加速度センサの傾斜出力値を微分しXY成分を2乗平方根をとったものを示しています。時刻表を見ると、「0分後 品川 → 11分後　新横浜 → 29分後　小田原 → 43分後　熱海 → 51分後　三島着」という感じです。もちろん、セットアップに若干の時間が掛かっていますので、その補正を行うと、大雑把に

-4分後 　品川9分後　新横浜27分後　小田原39分後　熱海47分後　三島着

という感じになると思います。よく眺めれば、停車時間(25-30分の間の「小田原での長い停車時間」とか)も見えてきますので、もう少し正確に走行場所に繋げることも簡単そうです。あぁ、携帯電話でGPS追尾をしておけばよかったですね。1分1回追尾なら、パケット代金もたいしたことないでしょうから。
　ちなみに、縦軸の値で15を超える辺りだと、PCのハードディスク保護回路が働いて、ハードディスクが停止する感じです。

■「醤油マヨネーズ」と「星形口」を繋ぐ粘性の秘密　

　「美味しさ・料理の科学」と言えば、上田氏によるレオロジー講座中で聞いた、色々なマヨネーズの粘性違いに関する話も面白かった。 たとえば、キューピーのマヨネーズに比べて、以前の味の素のマヨネーズは醤油とマヨネーズが作りにくかったという。 マヨネーズと醤油を混ぜ合わせようとしてかき混ぜても、なかなか上手く混じり合わなかったらしい。

　そこで、マヨネーズの粘度測定、つまりマヨネーズの「粘っこさ・流動しにくさ」を計り、「剪断応力（かき混ぜにくさ）の定常値の平方根」と「剪断速度（かき混ぜる速さ）の平方根」による散布図 "Casson Plot" (キャッソンプロット)にしてみると、その違いが切片、すなわち、降伏値（剪断速度を０にしたときの応力の平方根）の違いとして現れたという。味の素マヨネーズの方が、キューピーのものよりも、降伏値が大きく、剪断速度が遅い～停止状態の「流動しにくさ」が高かったらしい。なるほど、かき混ぜる速度が遅いときや、かき混ぜるのを止めたときの流動性が低ければ、確かに混ぜ合わすことは難しくなりそうだ。

　この「かき混ぜる速さ」に対する「かき混ぜにくさ」の違い、味の素マヨネーズとキューピーマヨネーズの違い、を生む原因は「マヨネーズに白身が使われているかどうか」であったという。

　現在と違って、かつては、

• キューピーマヨネーズ（黄身だけ）
• 味の素マヨネーズ（黄身＋白身）
• 味の素マヨネーズ ピュアセレクト（黄身だけ）

という違いがあったために、白身が混じっている味の素マヨネーズは（まるでメレンゲ状になるように）このような粘性を示したのだろう、ということだった。

　味の素マヨネーズが「降伏値」が大きいために醤油マヨネーズが作りにくい一方で、「降伏値」≒「剪断速度を０にしたときの応力」が大きいということは、容器から出てきたマヨネーズの形がなかなか崩れない、ということでもある。 つまり、容器の口が星形になっている容器から出されたマヨネーズであれば、星形断面のチューブ構造（のような姿）をなかなか変えない。 その結果、綺麗に映えるデコレーションをかつての味の素マヨネーズなら作りやすい、ということになる。たとえば、色とりどりのサラダを優雅に結ぶマヨネーズによる星型紐も、そんな原料・粘性の違いから生じることになる（のかもしれない）。『使いこなしにくい「不揃い」は美味しい。』と同じように言うならば、『かき混ぜにくいマヨネーズは形が崩れにくい』というわけだ。となると、結局のところ、よくある「長所と短所は同じこと」の１例である。

　醤油マヨネーズに向く「マヨネーズの粘性」や、サラダを綺麗に彩る「マヨネーズの粘性」など、食材物性や製造技術も勉強してみるととても面白く奥深いのだろう。 「醤油マヨネーズ」と「星形口」を繋ぐ味の素マヨネーズの粘性の秘密から、「長所と短所は同じこと」なんていうことも浮かび上がってくるように。