2008-06-29[n年前へ]
2010-08-01[n年前へ]
■免許更新時に配布される「交通の教則」で「安全運転の物理」を学ぶ!? 
先日の「事業仕分け」で話題になった、隠れたベストセラー「交通の教則」のページをめくっていると、面白いページに行き当たりました。それは、「5-2 自動車に働く自然の力」で、「車に働く自然の力」について書かれていて、軽く理系心をくすぐられる一節でした。たとえば、こんな風に、交通安全のための「科学」が説明されていくのです。
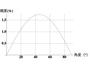
（カーブを曲がろうとする自動車に働く）遠心力の大きさは、カーブの半径が小さいほど大きくなり、速度の２乗に比例して大きくなります。
（追突時の）衝撃力は速度と重量に応じて大きくなり、また、固い物にぶつかるときのように、衝撃の作用が短時間に行われるほどその力は大きくなります。
例えば、時速60kmでコンクリートの壁に激突した場合は、約14mの高さ（ビルの5階程度）から落ちた場合と同じ程度の衝撃力を受けます。
制動距離や遠心力などは、いずれも速度の2乗に比例して大きくなります。速度が2倍になれば、制動力や、カーブで車の横すべりや転倒をさせようとする力は、2倍になるのではなく、4倍になります。
「衝突時の時速」を「ビルから落ちた時の高さ」に対応させて、衝突の衝撃を想像させるイラストなどもあって、で「交通安全の（ための）物理」を実感させられます。
「いらないからすぐ捨てる」という人も多いらしい「交通の教則」ですが、手渡されてしまったからには、「安全運転の物理」を楽しんでみるのも良いかもしれません。そのページを読むと、意外に捨てられずに家に持って帰る人も多くなるかも…しれません。
2011-12-01[n年前へ]
■ビリヤードの「バタフライ」トリックの「配置図」
「おっ？これは！」と驚かされるビリヤードのトリックショットに「バタフライ」があります。ビリヤード台の中央近くに６つの玉を置き、それらに手玉をぶつけ、一撃で６つの玉をすべてポケットに落とすというテクニックです。
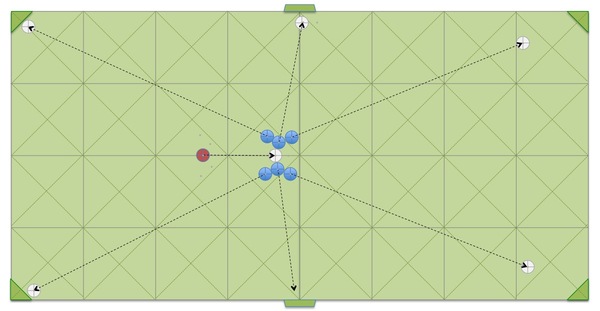
バタフライの玉配置をまずは単純に描いてみると、下図のようになります。左右対称に３つの玉をくっつけた状態で置き、左右にある３つの玉と３つの玉の（玉の大きさの2/3ほどの）隙間に手玉を打ち込む、という具合です。図を眺め、そして玉の動きを実際に眺めていると、玉配置の妙（たえ）に感嘆させられます。玉同士が衝突する際のズレやすべりを経て、６つのポケットへと玉が放射状に転がっていく動きを作り出す仕組みですが、実に絶妙です。（参考：スローモーション動画）
ビリヤードのゲームソフトなどは、こういう動きをどのように再現しようとしているのでしょうか？玉の動きを単に剛体球として計算しようとすると、このバタフライのようなトリックは再現することができないでしょう。だとすると、ボール同士の接触が時間をかけて行われるような（たとえば個別要素法のような）計算を（パラメータ調整などで）「らしく」適当に実装しているのでしょうか。
もしも、ビリヤード玉の衝突後の動きを予測・表示するAR Poolを使って、このバタフライトリックを眺めてみたら、一体どういう「未来予測」がされるのでしょうか？
それにしても、「単純なシステム」なのに驚かされること・面白いことが、世の中には意外に多くあるものです。
2013-02-15[n年前へ]
■隕石・流れ星は斜め４５°に降る確率が一番高い!?
「隕石・流れ星は斜め４５°に降る確率が一番高い!?」を書きました。（関連記事：あなたと見たい、流星群 ~ 同じ流星が見える距離）
すると、たとえば大気の厚みを１００ｋｍとすれば、地球への鉛直距離１００ｋｍを落ちる間に、大気に対して斜め４５°に侵入してきた隕石は約１００ｋｍ強ほど横方向にも飛んでいきます（すごく単純に言えば、単なる２等辺３角形ですからね）。 こんな計算をしてみると、流れ星や隕石が「斜めに大きく横切っていく」というイメージは現実を反映していそうだ、と気づかされます。
」など。