hirax.net::Keywords::「計算」のブログ

■「下向きにかがんだ時のおっぱい変形具合」を暗算計算する方法!?　

　おっぱいのヤング率が 0.5〜25×10^3 Pa 程度という数字を使うと、たとえば「下向きにかがんだ時のおっぱい変形具合」も大雑把に見積もることができます。（参考：「10%ゼラチン・ゼリーの柔らかさ」は「おっぱいより、ほんの少し堅いくらい」という必ず役に立つ豆知識!?）

　まずは、おっぱいの形状を１０ｃｍ四方の立方体として考えてみることにします。脂肪の密度は水より少し軽い程度ですから、このおっぱい立方体の重量は約1kgです。1kg重＝9.8Nの力が１０ｃｍ四方のおっぱいに働くということは、1m^2あたりの応力に直すと、これまた大雑把に見積もるならば、おっぱいを「伸ばす」向きに9.8 N / (0.1 m × 0.1 m) ≒ 1×10^3 Paの力が掛かるということになります。

　たとえば、おっぱいのヤング率を 1×10^3 Paとすると、

おっぱいの変形（歪み量）= 1×10^3 Pa/1×10^3 Pa =1

　ここで「実に面白い点」は、「地球上で（おっぱいに）働く重力がおっぱいのヤング率とほぼ同じ」という不思議な偶然です。言い換えれば、極めて興味深い点は、地球で生活するおっぱいの変形が数倍程度に収まるような特性になっている…という奇妙な事実です。

　…しかし、考えてみればその半分は必然です。なぜなら、おっぱいのヤング率が重力に対して小さかったら、誰しも「おっぱいが地面にまで垂れる垂乳根の母状態」になってしまい、ズリズリ…とおっぱいを引きずり歩くような生物が生存することはとても難しそうだからです。

　それでは、ヤング率が高い場合＝おっぱいが堅く変形しない場合にはどうか、なぜ堅いオッパイではなかったのか…ということについては、識者のご意見を拝聴したいところです。

■「胸先チラリ…」の幾何学!? ー Bカップ以下の小胸さんが要注意!という証明!?　

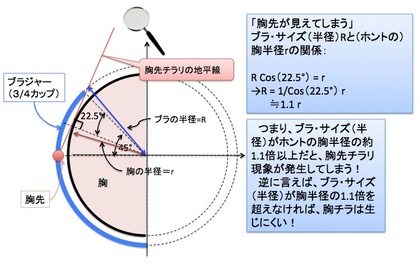　「胸先チラリ…」の幾何学!? ー Bカップ以下の小胸さんが要注意!という証明!?を書きました。

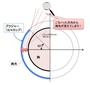
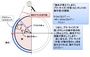
　アンダー65cmのCカップというのは、かなりレアなパターンでしょうから、実際のところ「胸先がチラリ見えてしまいやすいのは、A,Bカップにほぼ限られる」と言っても良いだろう、ということになります。

　というわけで、今回は単純な算数（数学）を使い「胸先チラリ…」の幾何学を考えてみました。数学的に導き出された結果は、胸先チラリ条件が生じるのは「ほぼBカップ以下の小胸さんに限られる！」という「なるほど、確かにそうかも！」という答えでした。

■ウォータースライダーで「水着ポロリ」しないためには「水着に1.5リットルのペットボトルを２本ぶら下げてもズレない」くらいにキツく締めることが必要だ！というマメ知識　

　もうすぐ夏が始まる…というわけで、先日、ウォータースライダーで「水着ポロリ」を生じさせる力の実験・計算をしました（ちなみに、今回の対象水着は、「ビキニ（セパレート）」タイプの水着です）。ウォータースライダーで滑り落ちる水着女性が、水面に突入する際の「相対速度」や「水着のさま」を動画像から解析し、その際の水面に対する相対速度から「水着に働く力」を計算する…というのがその概要です。

　その実験・計算結果は、水着の凸部に対して1平方ｃｍあたり約190グラム重の力が掛かり、水着全体では約4キログラム重の力がかかる…というものでした。つまり、ウォータースライダーで「水着ポロリ」しないためには「水着に1.5リットルのペットボトルを２本ぶら下げてもズレない」くらいにキツく締めておけば良い、というわけです。

　それでは、その力（ウォータースライダーで「水着ポロリ」させる力）を低減させるためにはどうしたら良いかとか、その力が働く方向と水着構造の組み合わせによる「ポロリ」しにくさについての考察…といったことは、また次回書いてみることにします。

■グラス片手に楽しく読めるシャンパンに関する計算や可視化解説　

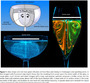
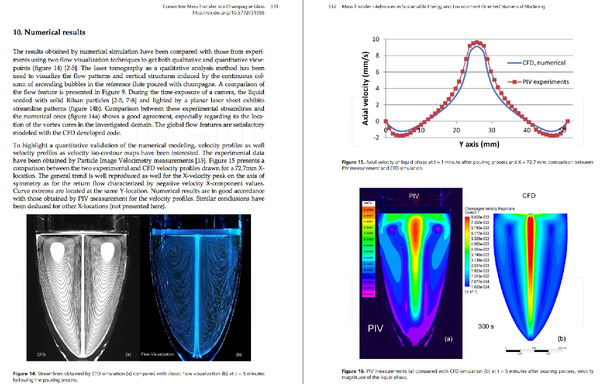
　普段はシャンパンなんて飲まないにも関わらず、クリスマスが近づくと風物詩的に少しだけ飲んでみたくなる。そんな時期に眺めてみるととても面白そうな「シャンパンに関する計算や可視化解説」があった。このConvective Mass Transfer in a Champagne Glass (Fabien Beaumont, Gérard Liger-Belair and Guillaume Polidori)が楽しいのは、登場する計算式が比較的簡単でわかりやすいということもあるけれど、何よりシャンパンが注がれたグラス内から立ち上る気泡を可視化したさまがとても美しく、その写真に思わず目を惹かれ、魅入られてしまうからだ。

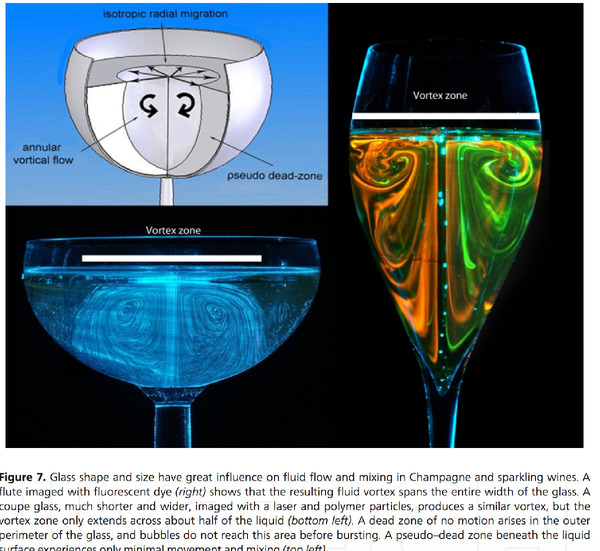
　アルゴンレーザーでシート状に光を照射して、シャンパンガラス周りでレーザー光が屈折してしまわないように、シャンパンを入れたグラスを水槽中に浮かべ、グラスを切断するように横から当てたレーザー光で浮かび上がらせた泡の動きは、ただ眺めているだけでも不思議に心地良くなる。

■Microsoft Excelで "=-1^2" が "-1"ではなくて"1"になる「理由」　

　Microsoft Excelで "=-1^2" が "-1"ではなくて"1"になるのが「なぜだろう？」というtweetを興味深く読み、そこから辿り着いた20年前のメーリングリスト記事が面白かったので、簡単なメモ書きをしてみます。メモ書きなので、面白い記事へのポインタと（その記事に対する）わずかな感想を書いただけの日記記事です。

　まず、この計算順にまつわる問題を考える時には、" Warning: Excel Performs Negation Before Exponentiation"のタイトルにもなっているように、Excelという一種のプログラミング環境上での、"negation"と"subtraction"という異なる2演算子の計算順序の違いを区別する必要があります。つまり、

=-A1^2

=1-A1^2

　次に、20世紀最後の年、つまり西暦2000年1月13日の20:18:46にDoctor Petersonがメールで書いている文面がとても参考になります。それは、"negation"のような単項演算子は”exponent”のような二項演算子に優先して演算されるものだったから、それをただ踏襲すると、こんな計算順序になるよね、というものです。「Lotus 1-2-3との互換性を重視した」わけではないけれど、プログラミング言語の過去経緯を踏まえて考える話だよね、というものです。

　そして何よりも、西暦2005年の12月16日にErikが書いているように、Windowsのメモ帳で "msgbox -2^2"と書いてから、そのファイルをtest.vbsという名前で保存して、もしもダブルクリックしたならば、（マイナス4ではなくて）"4"という答えが書かれたメッセージボックスを私たちは目にするよね。この例でもわかるように、エクセルの「ダメな話」として眺めるのではなくて、コンピューター科学の「興味深い話」として眺めるべき話じゃないか？というコメントが、とても参考になると思います。

So I think this isn't bad math on Excel's part, but good computer science.