hirax.net::Keywords::「クリスマス」のブログ

■Flash泣き笑い　

　今日見た二つのFlash。企業や公共のサイトでFlashを使う必要って全然無いと思うが、こんなのは好き。上は泣いて、下は笑った。（リンク）（リンク）

■何がきっかけになるか判らない。　

　ふと思い出したけど、中学時代の先生に三枝先生という人がいた。私達を教えていたときに既に定年の数年前だったが、その先生と較べてしまえば武田鉄矢や山下真司なんて本当にニセモノにしか見えないような感じの先生だった。私が中学を卒業してから4年後の冬の終わりに亡くなってしまったが、その先生が「グレてる生徒がマジメになるきっかけはほんのささいなことだったりする」と言っていた。

　それは、たとえば、母親が化粧っ気も無しに働いているところを眺めて、「母親に化粧をさせてやりたい」と思ったりするとか、そんなことだ。

　ふと思い出したそのきっかけが、ヒッキーのクリスマス（仮）だったということは内緒にしておこう。

■私と二度めに出会う「水」　

　Ohgimiさんと娘さんの会話から始まった話。さて、今年のクリスマスは雪が降るのでしょうか？（リンク）

■サンタが街にやってくる　

複数サンタクロースの巡回問題

　簡易に書き直した2011年版もあります。

　幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで（高原の診療所なのだから大して違いはないのだけれど）、とても不思議だった。

　さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。

　知らない人のために書いておくと、「巡回サンタクロース問題（TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
 

　これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが

• サンタクロース研究
• ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )

　そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。

　まず、始めに問題提起をしてみよう。

　「果たしてサンタは一人なのか？」

　どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。

　そこで、まずはサンタの歴史から調べてみると、Ｓａｎｔａさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。

　とはいえ、Ｓａｎｔａさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか？

　また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
 

全世界の人口増加の近似グラフ

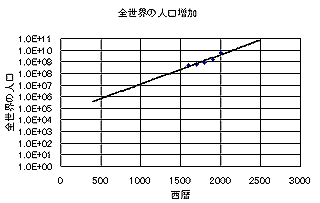　St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。

　サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。

　子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 

子供の家N=100までの場合のサンタが計算しなければならない経路の総数
横軸=N、縦軸=計算しなければならない経路数

　どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。

　先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。

　そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。

　それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
　一例として、サンタが1,2,10人の場合を示してみる。
 
 

複数サンタがいるときの
子供の家N=100までの場合のサンタが計算しなければならない経路の総数
横軸=N、縦軸=計算しなければならない経路数
黒=サンタが一人
緑=サンタが二人
紫=サンタが十人

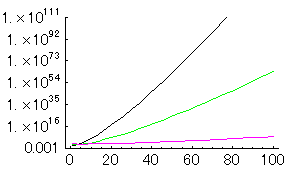　このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。

　実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。

　このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。

　ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。

　それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。

　ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。

　もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。

　こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。

　サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。
 

■私と二度めに出会う「水」　

クリスマスの小さな遺品

　先日、こんなメールを頂いた。

　私の娘は小学三年生。図書館から借りてきた「水の一生」といった、子供向け科学本（蛇口から出た水は下水を通って…<途中大幅に省略>…再度雨になって…というヤツです）を読んでおりました。そこで彼女はいくつかの疑問を口にしました。

「一度下水に流した水は、どのくらい経ったらまた私のところへ戻ってくるの？」
 

私　「必ずしもすべての水が海まで行くわけではなくて、下水処理場で蒸発して、川の取水口あたりで雨になる分子もあるはずだから、そうだなあ、一番早くて３日くらいかなあ。　勿論もっと長い場合もあるし、一度流したらキミが生きている間にはここには戻ってこない分子もあると思うよ」

「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」

私　「う〜ん…　　どれくらいなんだろう？」

　さて、どう思われますか？

　ところで、この後半の疑問「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」というのはたまに見かける話である。何かの小説で、「このコップの話が主人公が科学を志したきっかけになっている」という小道具に使われている例も読んだことがあるような気がする。

　たまに見かける話ではあるのだけれど、同じ本を読んでも人それぞれ抱く感想は違うし、私なりにも考えてみたい気もしたので、今回はこの「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」を考えてみることにした。

　人が一日に「出会う」水はどの位の量だろうか？成人男子が安静にした状態で、一日当たり大体2.5リットルの水を消費するという。すると、小さい子供の場合でも、少なくとも一日2リットルくらいは水を消費する、つまり水と「出会って」そして「分かれる」ことになる。2リットルの水というと、2000gだから、これを水の1molあたりの重さ18g /molで割って、さらにアボガドロ数（1mol当たりの分子数）をかけてやると、(2l = 2000g ) / 18g x 6.022x10²³個 = 6.7 x 10²⁵個となり、私たちが一日に出会う水分子の数の個数がわかる。

　この「とある一日に私たちが出会った水」が川へ流れて、海へ流れて、地球上にまんべんなく拡がったとしよう。地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は、いったいどのくらいの程度になるのだろうか？

　地球上の水は大体14億km³くらいだという。そのほとんどは96.5%は海水で、残りが陸地のさまざまな場所（そしてわずかに空気中）に存在している。この地球上にある水の重さを計算すると、14億km³= 1350000000km³ = 1.4 x 10⁹ x 10¹² kg= 1.4 x 10²⁴ g ということになって、これを水の1molあたりの重さ18g /molで割ってやると、地球上に存在する水分子の総量は 1.4 x 10²⁴/ 18 = 7.8 x 10²²mol ということになる。mol数から水分子の量に直すために、アボガドロ数6.022x10²³個/molをかけてやると、地球上の水分子の総量= 4.5 x 10⁴⁶ 個という数字が得られる。

　すると、地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は
「とある一日に私たちが出会った水分子」 / 地球上の水分子の総量 = 6.7x 10²⁵個 / 4.5 x 10⁴⁶ 個 = 1.5 x 10^-21= 0.00000000000000000015%というとても小さい割合になる。この割合は、新たに水分子と出会った時に、その水分子が「とある一日に私たちが出会った水」である確率と言い換えても良いだろう。とにかく、私たちの普段の生活の感覚からすれば、限りなく小さく思えてしまう。しかし、その再会の確率はとても小さく思えてしまうのだけれど、決して私たちは「とある一日に私たちが出会った水分子二度と水と再会しない」わけでは無いのである。

　例えば、180mlのコップ一杯の水の中には( 180ml = 180g ) / 18g x 6.022x10²³個= 6.0 x 10²⁴個の水分子が含まれている。ということは、このコップ一杯に含まれる水分子の中にいる、かつて「とある一日に私たちが出会った水分子」の数を計算してみると、
コップ一杯に含まれる水分子の数 x 「とある一日に私たちが出会った水」である確率= 6.0 x 10²⁴個 x 1.5 x 10^-21  = 9000個ということになる。コップ一杯の水の中にはかつて「とある一日に私たちが出会った水」が一万個近くも存在していることになる。

　しかも、この計算は「とある一日に私たちが出会った水分子」だけで計算していて、決して「これまでに私たちが出会った水分子」で計算しているわけではないのだから、「コップ一杯の水の中で、私と２度目に出会う水」はもっと多いことになる。もちろん、実際には私たちが消費した水が理想的に拡散したりはしないだろうから、こんな風に上手くはいかないだろうけれども。

　とりあえず、「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」という疑問を口にした小学校三年生の娘さんには、「ずっと昔のある日に出会った水がコップ一杯の中には一万個近くもあるかもね」と答えておくのが良いかもしれない。計算の中身、アボガドロ数なんて言っても、小学校三年生では「あぼがど？あぼがろど…？」と頭がこんがらがるだけかもしれないけれど、とりあえず「おとーさんって、何でもわかるんだー」とちょっとくらいは尊敬されたりするかもしれない。
 

　そういえば、先日東京で初雪が降った。「雪は天から送られた手紙」とは中谷宇吉郎の残した名言だけど、その雪を見ながらこんなことを考えた。

　ある日誰かが亡くなり、荼毘に付される。すると、その人の体のほとんどの部分は火と共に空へ昇っていくことだろう。成人の体のおよそ60%は水分だから、体重60kgの人であれば、その60%の36000gもの水が空へ還ってゆくことになる。その空へ還っていった水分子が世界中に散らばっていった後に、いつかまたその水分子と出会うためにはどの程度の水があれば良いだろうか？どの程度の水があれば、この中には「かつてあの人と共に空に帰っていった水分子」が一個くらいはある、と言えるものだろうか？

　これを先程と同じように計算してみると、ほんのちょっと「1 x 10^-3g」ほどの水があれば、その中には「かつてあの人と共に空に帰っていった水分子」が一個くらいある、という結果になる。「1x 10^-3g」ということは、大きさで言うと1mm³ほどになる。ちょうど雨粒一滴と同じ位の大きさだ。空から降ってくる雨一粒の中には「かつて亡くなった人と共に空に帰っていった水分子」が１個が漂っている、ということになる。

　冬の雪の一片の大きさが雨の一粒と同じくらいであるかは判らないけれど、今日のように何時の間にか雨が雪に変わることもあるくらいだから、やっぱり雪も雨と同じような大きさなのだろう。だとすれば、空から降ってくる雪の一片の中には、「かつて亡くなった人と共に空に帰っていった水分子」が１個宝石のように入っていてもおかしくはない。「雪は天から送られた手紙」であるならば、その中にはその手紙を天から送ってくる「かつて亡くなった人」のまるで遺品が１個づつ封じ込められているのである。「雪は天からの遺品」と言っても良いかもしれない。

　間もなく、クリスマス。そして、クリスマスには白い雪が付き物だ。空から舞い降りてくる白い雪の中には大切な１個の水分子「クリスマスの小さな遺品」が入っているのである。