hirax.net::Keywords::「セールスマン」のブログ

■鴻上尚史の「仕事の分類」「恋愛関係の分類」　

　鴻上尚史のドン・キホーテのピアス(668)に、俳優やミュージシャンになろうとする子供を応援する親が増えてきたことに驚きつつ、「きっちりした仕事」「浮き草のような仕事」や「実業」や「虚業」といった区別に意味のない時代になっていて、「やりたい仕事」「やりたくない仕事」くらいの区別しかできなくなっているのかもしれない、ということが書いてあった。

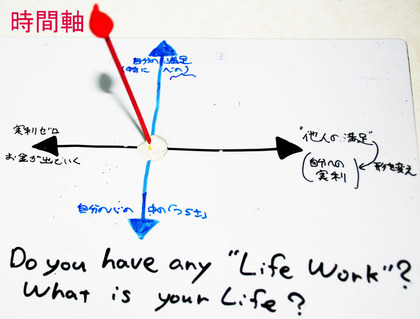
　もっと厳密に言うと、「やりたいけどやれない仕事」と「やれるけどやりたくない仕事」と「やりたくないけどやらなきゃいけない仕事」ということかな。
　おっ、まるで、恋愛関係みたいだ。
　鴻上尚史　ドン・キホーテのピアス(668)

　「「手作り三次元グラフ」と"Life Work"」や「"複雑極まりない"複素平面」上に「仕事」と「趣味」を描く」で作った分類（黒色の横軸＝"他人の満足"という軸。あるいは、その"他人の満足"が形を変えた”お金”といったもの、青色の縦軸は"自分(本人)の欲求・満足"を示す軸、赤色の軸は"時間軸"）に少し似ています。

　少し似てはいますが、鴻上尚史の分類には上のような分類とは決定的に違う・それはまさに決定的な軸がひとつ入っています。それは「やれるけれどやりたくない」と「やりたくないけどやらなきゃいけない」の間で迷い・決定するという「選択肢・意思」です。その選択や意思の軸が、鴻上尚史の分類では明確に描かれています。
　私が描いた三次元図では、もしも人がこの三次元中を移動していくように見る場合には、その人が（その人の仕事が）動く軌跡の過程の中にその選択肢が含まれているというわけです。

　俳優とかバンドマンどか、表現にかかわる仕事の多くは、「失業が前提」の職業になります。……「やりたくてやれる俳優の仕事」が来る日まで、「やれるけどやりたくない俳優の仕事」をするかどうか迷いながら、（「やれるけどやりたくない俳優の仕事」をするくらいなら、レストランのバイトなんかの）「やりたくないけどやらなきゃいけない他の仕事」で生き延びるのです。
　鴻上尚史　ドン・キホーテのピアス(668)

　ふと、私が描いた「自分の満足軸」と「他人の満足軸」が一致してしまったりすると、あるいは、その区別ができなくなってしまうと、「自分自身の満足」というものは得られない・見えなくなってしまうのかもしれない、と思う。

　この資本主義社会に生きている限り、商品とは、他人の欲望を具体化したものです。自分が作りたいだけでは、それは商品とはなりません。それが、他人が欲望するものとなって初めて商品となるのです。
　　　鴻上尚史「名セリフ！」文藝春秋社

　…問題がひとつだけあるとすると、優秀なセールスマンほど他人の欲望をまず一番に考え続ける結果、自分の欲望がわからなくなることです。いったい、自分は何がしたいのか、自分の人生の意味は何なのか、全くわからなくなるのです。
　　　鴻上尚史「名セリフ！」文藝春秋社

■「IronRuby」+「Mathematica Player」=「∞の可能性」　

　まだまだ、「(.NETで動くRubyである)IronRubyと(無料配布されている)Mathematica Playerの組み合わせ技」にハマっています。素晴らしく楽しく使うことができる言語環境Mathematicaと、やはり素晴らしく便利なRubyと、そして（多分便利な）.NETを一緒に用いることができるというのは、とてもエキサイティングな体験だからです。

　今日は、まずは「Mathematicaの使い方」を眺めながら、クラスタ分析をIronRuby+Mathematica Playerでなぞってみました。

include System
require 'Wolfram.NETLink'
include Wolfram::NETLink
kernelLink=MathLinkFactory.CreateKernelLink()
kernelLink.WaitAndDiscardAnswer()
result=kernelLink.EvaluateToOutputForm(
  'datarecords = {
{"Joe", "Smith", 158, 64.4}, 
{"Mary", "Davis", 137, 64.4}, 
{"Bob", "Lewis", 141, 62.8}, 
{"John", "Thompson", 235, 71.1},
{"Lewis", "Black", 225, 71.4}, 
{"Sally", "Jones", 168, 62.},
{"Tom", "Smith", 243, 70.9}, 
{"Jane", "Doe", 225, 71.4}};', 0)
result=kernelLink.EvaluateToOutputForm(
  'FindClusters[Drop[datarecords, None,
   {1, 2}] -> datarecords]', 0)
puts result
kernelLink.close

こうコードを書くと、各人の身長と体重のデータを用いて、それらの人を何グループかにクラスタリングを行うことが簡単にできます。たとえば、こんな結果が返ってきます。

{{{Joe, Smith, 158, 64.4}, {Mary,Davis, 137, 64.4}, {Bob, Lewis, 141, 62.8},{Sally, Jones, 168, 62.}}, {{John,Thompson, 235, 71.1}, {Lewis, Black, 225, 71.4}, {Tom, Smith, 243,70.9}, {Jane, Doe, 225, 71.4}}}

見事にクラスタリングされています。もちろん、これは、Mathematicaのマニュアルそのままのコードです。けれどそんな処理をRubyで行うことができて、その結果をRubyでさらに使うことができるのはとても便利です。

あるいは、

include System
require 'Wolfram.NETLink'
include Wolfram::NETLink
kernelLink=MathLinkFactory.CreateKernelLink()
kernelLink.WaitAndDiscardAnswer()
result=kernelLink.EvaluateToOutputForm(
  'FindShortestTour[
{{4, 3}, {1, 1}, {2, 3}, {3, -5}, 
  {-1, 2}, {3, 4}}]', 0)
puts result
kernelLink.close

なんていうコードを書けば、二次元座標群を「どうすれば最短時間（距離）で巡ることができるか？」という巡回セールスマン問題を解くことができます。もちろん、答えはすぐ返ってきて、

{11 + Sqrt[2] + Sqrt[5] + 3 Sqrt[10],
 {1, 3, 5, 2, 4, 6}}

というように、「最短距離」と「どのように点（都市）を廻れば良いか」がたちどころにわかります。

　クラスタ分析、巡回セールスマン問題・・・ありとあらゆる問題を、IronRubyとMathematica Playerのタッグは解いてくれます。「IronRuby」+「Mathematica Player」を使っていると、「∞の可能性」を実現できるような「錯覚」を覚えます

■「科学的に物を見る目」と「広い視野」　

　講談社文庫を読むときは、いつも、巻末にある野間省一による「刊行の辞」を読み返します。なぜかと言えば、そのアジテーションにひどく心を揺り動かされるからです。

　講談社と言えばブルーバックスという理科趣味人も多いかもしれません。ブルーバックスと言えば、「サイエンス風味（っぽさ）がトッピングされた娯楽（エンターテイメント）本」です。いわば、今の科学新書ブームのさきがけです。そのブルーバックスの巻末、「発刊のことば」には「科学をあなたのポケットに」と題して、こんなやはり野間省一による言葉が掲げられています。

　二十世紀最大の特色は、それが科学時代であるということです。科学は日に日に進歩を続け、止まるところを知りません。一昔前の夢物語もどんどん現実化しており、今やわれわれの生活すべてが、科学によってゆり動かされているといっても過言ではないでしょう。
　そのような背景を考えれば、学者や学生はもちろん、産業人も、セールスマンも、ジャーナリストも、家庭の主婦も、みんなが科学を知らなれば、時代の流れに逆らうことになるでしょう。
　ブルーバックス発刊の意義と必然性はそこにあります。このシリーズは、読む人に科学的にものを考える習慣と、科学的に物を見る目を養っていただくことを最大の目標にしています。そのためには、単に原理や法則の解説に終始するのではなくて、政治や経済など、社会科学や人文科学などにも関連させて、広い視野から問題を追及していきます。

　この1963年9月に書かれた文字、50年近く前に書かれた宣言を読む時、学者や学生はもちろん、産業人も、セールスマンも、ジャーナリストも、家庭の主婦も…、心の琴線に何かが触れるように感じる人も多いのではないでしょうか。

■巡回セールスマン問題の答が描く「一筆書きアート」　

　一年ほど前、「数百個の数字をエンピツで結んでいくアニメーション」を作ってみました（”点と点を結んで行くと浮かびあがる”スティーブ・ジョブス）。

　この"Connecting the dots"な一筆書きラクガキ…「散らばっているたくさんの点たちを結んでいく絵」は、ペン先が何回も・何度も同じような場所を往復しています。つまり、右往左往が繰り返される、あまり効率的でない「描き方」です。

　もしも、たくさんの点が散らばっている時、それらの点を「一番効率的に」「最も最短で描く」にはどうしたら良いでしょう？…ということを考え始めると、それは「巡回セールスマン問題」という問題に変わります。

　巡回セールスマン問題（じゅんかいセールスマンもんだい、Traveling Salesman Problem、TSP）は、都市の集合と各2都市間の移動コスト（たとえば距離）が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路の総移動コストが最小のものを求める（セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める）組合せ最適化問題である。

巡回セールスマン問題

　"TSP ART"（＝巡回セールスマン問題的アート）と画像検索すると、数多くの街を廻るセールスマンのように、たくさんの点群を結ぶという作業を、最も効率的に行った「たくさんの一筆書き」アートを見ることができます。画像の「濃い部分」に「”たくさんの点”」がばらまかれているようにした上で、それらの点を最も効率的に結んでいくのがTSP Artです（参考：TSP Art）。

　この巡回セールスマン問題的アート（TSP Art）を描くのは結構大変です。何しろ、たとえば16階調で256×256の絵を描こうとすると、16×256×256…つまり1万048千576の点を「辺り一帯」にばらまいて、その1万048千576もの点を最も効率的に移動するにはどうしたら良いか？という超大規模な巡回セールスマン問題を解かなければならないからです。

　しかし、巡回セールスマン問題的「一筆書きアート」は大変でありつつ、とても素朴で魅力的です。こんなラクガキ、何だか少し描いてみたくなりませんか？