hirax.net::Keywords::「クラスタ分析」のブログ

■『理系サラリーマン 専門家11人に「経済学」を聞く! 』　

　「個性溢れる11人の経済学者の方々に話を聞く」という趣旨の本、『理系サラリーマン 専門家11人に「経済学」を聞く! 』が発売されました。大竹文雄・玄田有史・友野典男・松原隆一郎・小島寛之・奥村宏・西村和雄・森永卓郎・中島隆信・栗田啓子・中村達也という、11人の経済に関わる方々が、ものわかりの悪い生徒に実に丁寧に教えてくれたこと、その内容が本になりました。

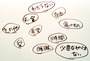
　本書には、一般の方々や経済学者の方々のアンケートから、「経済学者」「一般のひと」がそっくりだけれど、ほんの少しだけ違う姿が浮かび上がり、「豊かになるために必要なもの」をクラスタ分析した結果から、「希望とか自由とか愛」といった見えないものの繋がりを眺めたりすることができるオマケもついています。また、産業・科学や芸術・宗教といった歴史背景と、経済学の世界地図の上に時系列で並べた「歴史年表」もついています。

　豊かになるために、小島先生はたくさんのものを選び、(「若い頃は時間があるけれど金がなかった。今は時間だけが必要…つまりは年をとったということです」といった言葉とともに)大竹先生と友野先生は時間だけを必要とし、森永先生は「愛」だけを選びました……

　一般の方々や経済学者の方々へのアンケート結果、そこに記された言葉を眺めていると、不思議なほど私たち自身（そして私たちの分身のような経済学者の方々）の姿が見えてきます。そんな私たち自身の姿・私たち自身が望むことを眺めつつ、経済学者の先生方が話すこと読むのも、一興かと思います。

■続々・『理系サラリーマン 専門家11人に「経済学」を聞く! 』　

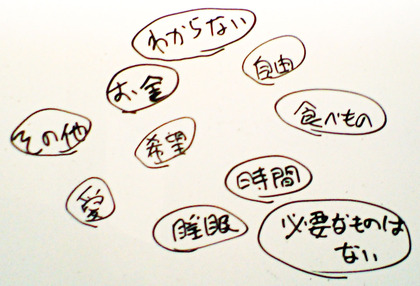　『理系サラリーマン 専門家11人に「経済学」を聞く! 』を出す際に、200人の人たちに「あなたが豊か・幸せになるために必要なものは何ですか？」と尋ねてみました。右に走り書きしたような「自由」「お金」「食べもの」「時間」といった選択肢を並べ見せながら、その人が豊か・幸せになるために必要なもの、を尋ねてみたのです。

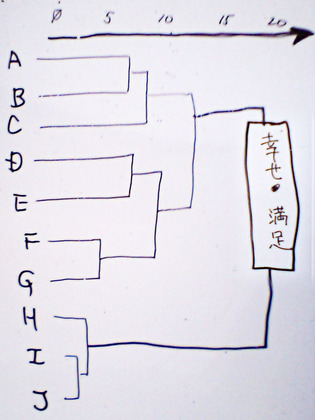　そして、amazonで表示される「お勧め本」やはてなダイアリの「お勧めページ」を算出するのと同じように、つまりはその選択肢を選んだ人の重複度合いなどを計算し、クラスタ分析をした結果の樹形図が右のようになります。右の図ではA,B,C……などのように記号で書いたありますが、もちろん、本の中でもアルファベットが書いてあるわけではなく、「お金」「睡眠」「時間」といったものがクラスタ分析・表示されているわけです。つまりは、「クイズの答え」を知りたくなったら、本書を手にとりそのページを眺めてみて下さいね、ということになります。

　「貨幣とは鋳造された自由である」というのはドストエフスキーの言葉ですが、クラスタ分析の結果は、見事なまでに「お金」と「自由」の距離や、「愛」や「希望」の距離を算出しています。右の図のA,B,C,D,……といった記号が「一体どんな言葉」なのか予想をしてみて、そして回答編を書店で眺め・楽しんで頂けたら幸いです。

■「IronRuby」+「Mathematica Player」=「∞の可能性」　

　まだまだ、「(.NETで動くRubyである)IronRubyと(無料配布されている)Mathematica Playerの組み合わせ技」にハマっています。素晴らしく楽しく使うことができる言語環境Mathematicaと、やはり素晴らしく便利なRubyと、そして（多分便利な）.NETを一緒に用いることができるというのは、とてもエキサイティングな体験だからです。

　今日は、まずは「Mathematicaの使い方」を眺めながら、クラスタ分析をIronRuby+Mathematica Playerでなぞってみました。

include System
require 'Wolfram.NETLink'
include Wolfram::NETLink
kernelLink=MathLinkFactory.CreateKernelLink()
kernelLink.WaitAndDiscardAnswer()
result=kernelLink.EvaluateToOutputForm(
  'datarecords = {
{"Joe", "Smith", 158, 64.4}, 
{"Mary", "Davis", 137, 64.4}, 
{"Bob", "Lewis", 141, 62.8}, 
{"John", "Thompson", 235, 71.1},
{"Lewis", "Black", 225, 71.4}, 
{"Sally", "Jones", 168, 62.},
{"Tom", "Smith", 243, 70.9}, 
{"Jane", "Doe", 225, 71.4}};', 0)
result=kernelLink.EvaluateToOutputForm(
  'FindClusters[Drop[datarecords, None,
   {1, 2}] -> datarecords]', 0)
puts result
kernelLink.close

こうコードを書くと、各人の身長と体重のデータを用いて、それらの人を何グループかにクラスタリングを行うことが簡単にできます。たとえば、こんな結果が返ってきます。

{{{Joe, Smith, 158, 64.4}, {Mary,Davis, 137, 64.4}, {Bob, Lewis, 141, 62.8},{Sally, Jones, 168, 62.}}, {{John,Thompson, 235, 71.1}, {Lewis, Black, 225, 71.4}, {Tom, Smith, 243,70.9}, {Jane, Doe, 225, 71.4}}}

見事にクラスタリングされています。もちろん、これは、Mathematicaのマニュアルそのままのコードです。けれどそんな処理をRubyで行うことができて、その結果をRubyでさらに使うことができるのはとても便利です。

あるいは、

include System
require 'Wolfram.NETLink'
include Wolfram::NETLink
kernelLink=MathLinkFactory.CreateKernelLink()
kernelLink.WaitAndDiscardAnswer()
result=kernelLink.EvaluateToOutputForm(
  'FindShortestTour[
{{4, 3}, {1, 1}, {2, 3}, {3, -5}, 
  {-1, 2}, {3, 4}}]', 0)
puts result
kernelLink.close

なんていうコードを書けば、二次元座標群を「どうすれば最短時間（距離）で巡ることができるか？」という巡回セールスマン問題を解くことができます。もちろん、答えはすぐ返ってきて、

{11 + Sqrt[2] + Sqrt[5] + 3 Sqrt[10],
 {1, 3, 5, 2, 4, 6}}

というように、「最短距離」と「どのように点（都市）を廻れば良いか」がたちどころにわかります。

　クラスタ分析、巡回セールスマン問題・・・ありとあらゆる問題を、IronRubyとMathematica Playerのタッグは解いてくれます。「IronRuby」+「Mathematica Player」を使っていると、「∞の可能性」を実現できるような「錯覚」を覚えます

■「転職したい企業ランキング」をクラスタ分析してみる　（初出：2006年02月21日）　

「エンジニア3000人大調査！転職したい企業ランキングBEST10」という記事を読みました。「エンジニア3074人に向けて実施した転職に関する意識調査をもとに、エンジニアが転職したい企業と理由を明らかにする」というものです。そこには、アンケート結果から「転職したい企業ランキング」と「その企業を選んだ代表的な三つの理由」が挙げられています。

　そこに書かれている「理由」は、それらの企業で働いている人たちではなく、転職先としての「イメージ」です。そのイメージは、実際には、その企業の実情とは異なっているのかもしれません。

　しかし、「その企業へ行きたいと思う人たち（未来のその企業の社員）の意識・指向」がそこに示されていると考えてみれば、そういった「イメージ」も、ある程度は、それらの企業の雰囲気と遠くないものだ、という見方もできそうです。

　ところで、記事中では「転職したい企業トップ10 (とその理由)」が挙げられているのですが、そのランキングをただ眺めているだけでは、今ひとつ特徴が見えてきません。たとえば、挙げられている企業の特徴などは、眺めているだけでは、なかなかわかりません。

　 　そこで、「転職先として選んだ理由」をもとに、各企業に対してクラスタ分析をしてみました。その結果が右上の図になります。この図では、左側に各企業が(縦に)並んでいて、似ている（近い）企業どうしが線で（左から順に）結ばれていきます。

　たとえば、トヨタ自動車と日本電気は、とても似ているのようで、わりにすぐ（左の位置で）線で繋がっているのがわかるはずです。また、トヨタ自動車と日本IBMなどはかなり遠く（似ておらず）ずいぶん後になってから（つまりは、右の位置で）ようやく線で繋がっていることがわかると思います。こうして眺めてみれば、各企業の特徴や似ている企業探し、などが簡単になります。

　例を挙げると、トヨタ自動車と日本電気の「繋がり」は「長期的な安定性」繋がり、です。また、上半分のグループは「給与・待遇がよさそう」繋がりで、下半分のグループは「技術者が働きやすい環境・設備」繋がり、です。…とそんな風に眺めていくと、色々なことが見えてきます。

　ちなみに、この記事を眺めながら、「このランキング中に登場しているある企業の社員の方」に、「この中に転職したい企業はあります？」と聞いてみました。すると、その人は「このクラスタ分析で（その人の勤める企業と）隣あっていた二つの企業（本田技研工業と日本IBM）」を挙げたのです。ということは、「自分が入りたい企業」を眺めるとき、意外このクラスタ分析の結果は役に立つものかもしれません。

　あなたなら、どの企業に転職・入社してみたいと思いますか？もしも、このクラスタ分析結果に示されている会社で働いている方がいたら、この結果をを眺めたとき、どんなことを思うでしょうか？

■身長とスリーサイズでアイドルをクラスタリングしてみよう!?　

　「アイドルプロフィール（スリーサイズ、カップ情報）」のデータを使い、各アイドルを「身長・B・W・H」という４次元情報をもとにクラスタリング（クラスタ分析）してみました。登場するアイドルは総勢395人！ということで、解析した結果はテキストファイルとしてここ（idolClusters.txt）に置いておきます。

　２０クラスタほどに「分けて」はみたものの、果たして「上手く分かれている」のか「ほどよく分かれているわけでないのか」…それが全くわかりません。アイドルの顔を見ることはあっても、あまり身長やスリーサイズは眺めたり意識したりといったことをしていないのかもしれません。

{{{"逢沢りな"}, {"岡安麗奈"}, {"川村虹花"}, {"小池里奈"}, {"小池凛"}, {"指原莉乃"}, {"澤田リサ"}, {"志田友美"}, {"高柳明音"}, {"久本彩奈"}, {"渡辺麻友"}, {"黒川智花"}, {"酒井萌衣"}, {"戸田恵梨香"}, {"中田彩"}, {"平嶋夏海"}, {"福田沙紀"}, {"前田敦子"}, {"前田希美"}, {"松井玲奈"}, …（中略）…{"七色あん"}, {"MARI"}, {"中川朋美"}, {"水樹たま"}}}

　ざっと眺めると、"MEGUMI"や"手島優"は、同じクラスタ（グループ）だと自然に納得できますが、これは「アイドル」とはいっても「グラビアアイドル」という属性を持つがためにスリーサイズ的なイメージが頭に浮かぶ、のかもしれません。