2008-05-11[n年前へ]
■腹部全脂肪面積減少のヒミツ 
こんなキャッチフレーズの新聞広告を見た。
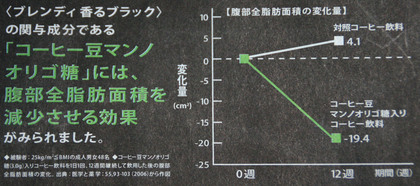
「コーヒー豆マンノオリゴ糖」には、腹部全脂肪面積を減少させる効果がみられました。そこには、(成人男女が)缶コーヒーを一日一回飲むことで、12週間のうちに20cm^2ほど「腹部全脂肪面積」が減少しているグラフが掲載されていた。そのグラフによれば、「比較対照のコーヒー飲料」を一日一回飲んでいた場合には、-4cm^2ほど「腹部全脂肪面積」が増加している結果が示されている。
「腹部全脂肪面積」とは一体どのようなものだろうか?……単純にそれを想像するなら、それは「腹巻で腹部を巻くようにしたときの円筒状の部分の表面積」に思える。もし、そうであるならば、このグラフは次のような結果に見えてくる。
「腹巻で腹部を巻くようにしたときの円筒状の部分の表面積」は
高さ(cm)×2×3.14×腹部の半径(cm)である。腹部の高さは、成人男女であれば20cmほどだろう。そこから逆算して見ると、20cm^2ほどの「腹部全脂肪面積」減少は、0.16cm=1.6mmほどの腹部の半径(脂肪厚み)減少を示すことになる。たった、1.6mmの変化である。
と書くと、いかにもの「数字のマジック」でしかないようにも思える。しかし、「(腹部に巻く)ベルトの長さの変化」でそれを表現すると、それは1cmほどになる。そう考えて見ると、今度はこの脂肪減少量が結構大きいものに感じられてくる。何しろ、ベルトの穴一個分ほどの量である。
ちなみに、「比較対照のコーヒー飲料」を一日一回飲んだ場合の「4cm^2ほどの腹部全脂肪面積増加」は、30μmほどの腹部の半径(脂肪厚み)増加を示している。30μmでは髪の毛の太さにも満たない程度の変化である。ここまでくると、誤差としか言いようのない範囲に思える。
結局のところ、「よくわからない」としか言いようがないが、次にコーヒーを買うときには、この広告が気になって(この)「体脂肪が気になる方に」のコーヒー飲料を買ってしまいそうな気がする。もっとも、「20cm^2ほどの腹部全脂肪面積減少」よりは、「一月でベルトの穴1つウェストが細くなる」という売り文句の方が実感できそうな気もするのだが。
2008-05-12[n年前へ]
■続・腹部全脂肪面積減少のヒミツ 
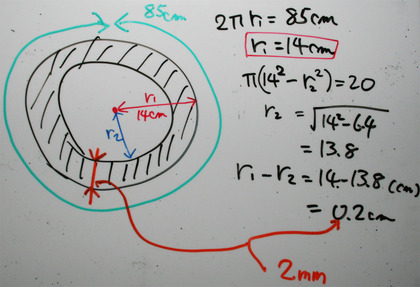 「腹部全脂肪面積減少のヒミツ」を書いた後に、もしかしたら「腹部全脂肪面積」というのは、腹部の断面を撮影した際の「脂肪の断面積」を表しているのかもしれない、とふと考えた。つまり、右の胴体輪切り画像で言うところの「斜線部分=腹部全脂肪面積」なのかもしれない、と考えた。
「腹部全脂肪面積減少のヒミツ」を書いた後に、もしかしたら「腹部全脂肪面積」というのは、腹部の断面を撮影した際の「脂肪の断面積」を表しているのかもしれない、とふと考えた。つまり、右の胴体輪切り画像で言うところの「斜線部分=腹部全脂肪面積」なのかもしれない、と考えた。
腹部断面の脂肪断面積を「全脂肪」と言うのも不思議な感じがするし、それを「面積」と言うのもまた奇妙な気がするけれど、ふとそう考えた。そこで、「腹部全脂肪面積」が腹部断面における「脂肪の断面積」だった場合に、
20cm^2ほどの「腹部全脂肪面積」減少がどの程度の脂肪厚み変化に相当するかを計算してみた。
すると、たとえばウェスト(腹部周囲長)が85cmの人であれば、20cm^2ほどの「腹部断面積」の変化は、腹部の半径(脂肪厚み)が2mm減少することに相当することがわかる。ということは、「腹部全脂肪面積」=「腹巻で腹部を巻くようにしたときの円筒状の部分の表面積」とした時の昨日の計算結果、すなわち、腹部の半径(脂肪厚み)が1.6mm減少する、という結果と大して違いがないものになる。
……とはいえ、脂肪厚みが2mm弱減少する、つまり、ベルトの穴で一つ細くなる、というのは(それが本当であれば)結構魅力的である。一体、香るブラック ブレンディの「コーヒー豆マンノオリゴ糖」のちからが示す「腹部全脂肪面積」は何を示しているのだろうか。
2010-11-08[n年前へ]
■"orz"より"oπ"を使おう!? 
 "orz"という文字に形はとても似ているけれど、もっと形が好きなのが"oπ"だ。一文字目は"orz"と同じアルファベットの"オゥ"で、2文字目はこれすなわちギリシア文字の"π"だ。つまり、円周率のパイである。パイアール二乗のパーイである。
"orz"という文字に形はとても似ているけれど、もっと形が好きなのが"oπ"だ。一文字目は"orz"と同じアルファベットの"オゥ"で、2文字目はこれすなわちギリシア文字の"π"だ。つまり、円周率のパイである。パイアール二乗のパーイである。
"oπ"は形が実に情けない。そして、発音しようとすると、この発音がまた気恥ずかしく情けない(発音的には"オゥ"より、"オ"の方が良いかもしれない)。しかし、読み方がよくわからない"orz"よりは、恥ずかしくて発音できなくても、少なくとも読み方がわかる"oπ"の方が心地良いような気がする。
だから、"orz"より"oπ"を使おう、と思うのである。
2010-12-01[n年前へ]
■「地球の大きさ」と「ウェスト周りの脂肪」の不思議!? 
 前から不思議に思っていることがあります。それは、同じ現象であっても、その対象次第で(それが)「とても小さく思えたり」「とても大きく思えたり」する、ということなのです。
前から不思議に思っていることがあります。それは、同じ現象であっても、その対象次第で(それが)「とても小さく思えたり」「とても大きく思えたり」する、ということなのです。
その不思議が一体どんなことかといえば、それは「円の直径がn増えたとき、円周はどれだけ増えるか」というお題なのです。
たとえば、ウェスト周りの脂肪の厚みが1cm増えただけで(つまり、太れば)、ウェストに巻くベルトは約6.3cmほども長いものが必要になります。脂肪の厚みがたった1cm増えただけで、6cm強ほどもベルトの穴の位置や、スカートのウェスト周り長さが増えてしまうのです。それは、
円周=2×π(パイ)×r(半径)
という公式を考えてみれば当たり前の話ですが、それは意外なほど大きく感じる変化ではないでしょうか?
 その一方で、それがこういう話ならどう感じるでしょうか?「地球の半径が1m大きくなったら、地球一周分の長さは一体どう変わるでしょう?」・・・さて、あなたは一体どんな風に感じたでしょうか?
その一方で、それがこういう話ならどう感じるでしょうか?「地球の半径が1m大きくなったら、地球一周分の長さは一体どう変わるでしょう?」・・・さて、あなたは一体どんな風に感じたでしょうか?
もちろん、それは先ほどのお題と同じく、
円周=2×π(パイ)×r(半径)
なのですから、地球一周の長さは6m強ほど長くなります。・・・たった、地球の半径が1m増えても地球の周りは6mしか増えないのです。この変化を意外なほど小さく感じる、という人も多いのではないでしょうか。
 ウェスト周りの脂肪と地球の大きさ、どちらも同じ話しなのに、一方はとても大きく感じ・一方はとても小さく感じます。この違いは一体何が生み出しているのでしょう?
ウェスト周りの脂肪と地球の大きさ、どちらも同じ話しなのに、一方はとても大きく感じ・一方はとても小さく感じます。この違いは一体何が生み出しているのでしょう?
人の感じ方、「どれだけ細かなものを気にするか」というようなことは、眺める対象の大きさ次第で変わるように思います。「地球の大きさ」と「ウェスト周りの脂肪」の不思議も、そういう観点から考えてみれば、とても自然に思える現象なのかもしれません。そんなことを考えてみれば、意外に面白いことを見いだせるように思うのです。
2012-01-08[n年前へ]
■「迂回し余る道」や「余る何かを導く何か」 
 十年一昔、と言います。十年というのはとても長いようでいて、それと同時に、思うよりずっと短い…そんな時間です。十年以上、WEB上で日記を書き続けていれば、色々あるものです。 from 「n年前へ」
十年一昔、と言います。十年というのはとても長いようでいて、それと同時に、思うよりずっと短い…そんな時間です。十年以上、WEB上で日記を書き続けていれば、色々あるものです。 from 「n年前へ」
本当の理科人間は理屈を言い争うディベートを好みません。どんな結論にも理屈はつけられるので、このようなコトバによる議論が、意味ある結論に導くとは思わないからです。
中学時代、「グレてる生徒がマジメになるきっかけは、ほんのささいなことだったりする。けれど、それが大事なことなんだ」と老先生が言っていた。それは、たとえば、母親が化粧っ気も無しに働いているところを眺めて、「母親に化粧をさせてやりたい」と思ったりするとか、そんなことだった。
道が柔らかく曲がっている。ゆったりと左に右に道が方向を変えている。そんな時、昔の街道の雰囲気を感じる。そして、その道端のどこかには、必ず寺社や祠がある。
坂村健は「新技術が研究されてから一般化するまでに二十年かかる」と言う。つまり、その当時の新技術が今現在2005年の世界を支えている(あるいは近い未来に支えていく)ことになる。科学技術の発展はそんなに速くない。科学技術を作っている側も使っている側も、時の流れはドッグイヤーであるかのように早いように思えるかもしれないが、実はそんなに速くない。
むしろ、いとうせいこう氏のような(数式を言葉とみなせない)文科系作家は、言葉の厳密な意味からもれてしまいがちなある種の感情や雰囲気といったものを表現していくのが主たる仕事ではないんだろうか。
これらの小説は、昭和初期という舞台上に、”今”という瞬間が描かれている。だから、小説に登場する登場人物たちは、”今”を生きる私たち自身である。…”今”を生きる私たちに向けて発せられた「ひとこと」に、少しばかり、目を通してみるのも良いと思う。