hirax.net::Keywords::「OpenFOAM」のブログ

■「エアロ」が売りな自転車は"空気抵抗（圧力）分布例"をカタログに載せて欲しい!？　

　「軽~い自転車が欲しい」と思ったりする時、「おいおい、自分の体重（脂肪）を減らす方が効率いいだろ？」という声が聞こえます。そしてまた、「一切ムダの無いエアロ形状」なんて謳った宣伝文句に目を奪われた時には、「自転車はエアロでも、そこにまたがってる”ボディ”がエアロじゃないから！」というツッコミが聞こえてきます。

　数値計算フレームワークのOpenFOAMのチュートリアル、走るオートバイの空気抵抗を求めるサンプルを動かし、バイクの各部分が受けてる空気抵抗（圧力）を眺めてみると、空気にぶつかっていく先端部分に（空気抵抗は）ほぼ集中しているよなぁ…と感じさせられます。たとえば、上の画像はバイクや乗員が受ける圧力を色で示し、さらに空気が流れる流線を重ねたものですが、空気を切り裂く先端部分に圧力がほぼ集中していることがわかります。

　「エアロ形状」を売りにする自転車などは、こんな"空気抵抗（圧力）分布例"をカタログに載せるといいのではないかと思います。そんなデータを眺めれば、自転車・乗員含めた上での「この風に・こんな程度（量）、空気抵抗が低減できているんですよ（こんな体型・姿勢の人ならね）」といったメリットがわかりやすくなるような気がします。あるいは、メリットがあまりなさそうであれば、買ってから後悔することも少なくなるように思います。

■「時速60kmの風を受ける感触」を真面目に計算しても、やはり「ウィダーゼリー１パック」と同じくらい！？　

　「時速60kmの風」は「アンダー85cm Cカップを1.3mm押し込む感触」で「ウィダーゼリーの重さ」とほぼ同じ!?という法則で書いたように、非粘性流体のエネルギー保存則であるベルヌｰイの定理を使うと、「掌（てのひら）が時速60kmの風を受ける時、掌にはおよそ170 Pa 程度の圧力がかかる」ということを解析近似式から得ることができます（参考：計算方法は「風でめくれるスカート」の科学！「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートは必ずめくれる!?の法則にあります）

　ちなみに、掌の大きさが10cm四方…つまり0.01m^2だとすると、170 Paの圧力を受ける掌は1.7 N = 0.170kg重の力を受けます。つまり、時速６０kmの風を掌に受ける時、あるいは、アンダー85cmCカップのおっぱいを1.3mmほど押し縮める時、掌はウィダーゼリー（１パック１８０ｇです）を載せた時と同じ程度の力を受けるのです。…それを逆に言うならば、「ウィダーゼリーの重さ」がわからなかったら、アンダー85cmCカップのおっぱいを1.3mmほど押し縮める時の感触を思い出せば良い、というわけです。

　今日は、風を受ける掌の周りの空気流の動きを真面目に計算し、「掌の感触」を（以前行った）解析近似解と比べてみることにしました。…というわけで、下の一連の画像が、掌モデルに風を当ててみたところです（ちなみに、今回の計算は時速６０kmで行うつもりが、間違えて時速73kmで行っていました）。

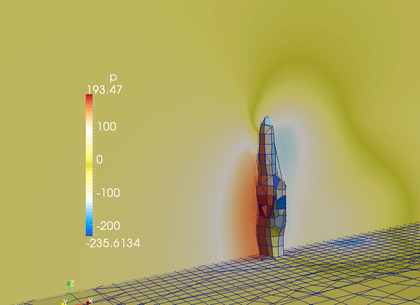
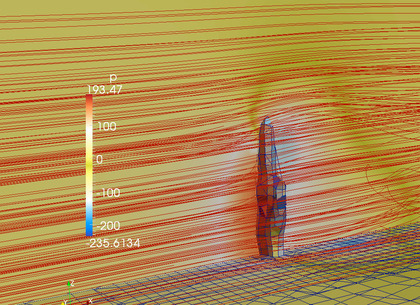
　空気流の圧力を表示してみた結果（たとえば左の画像）を眺めれば、掌の前後にはおよそ３００パスカルの圧力差があることがわかります。時速60kmの風速を計算するつもりが間違えて時速７０kmで行っていたことを考えれば、（これを時速６０kmの時に換算すると）ざっくり300パスカル　×　（時速60km／時速72km ≒ 250パスカル というところでしょうか。

　解析近似により見積もった掌前後の圧力差が170パスカルで、数値シミュレーションによる圧力差が250パスカル程度…どちらも大雑把な計算であることを考えれば「どちらも大体同じ」と言って良いくらいかもしれません。

　というわけで、今日行った「掌周りの空気流の真面目な計算」からも、「時速60kmの風を受ける感触」を真面目に計算しても、やはり「ウィダーゼリー１パック」と同じくらい、という結果が得られたようです！？

■「ギネスビールの下に沈む泡」をOpenFOAMで計算してみよう!?　

　　ビールをグラスに注ぐと、「グラスの中の泡は上に浮かび上がっていく」のが普通に思えます。けれど、たとえば、ギネスビールをグラスに注ぐと、グラス中で泡が下へ下へと沈んでいくさま（ギネス・カスケード）を見ることができますし、実はギネス以外のビールや水ですら、そんな「下に沈んでいく泡」を見ることができます（参考：ギネスビール風「下に沈む泡」を作るコツ）。

　ビールを心から愛してる知人が、フリーのシミュレーションソフトウェア（開発プラットフォーム）であるOpenFOAMを使って、「ギネスビールの下に沈む泡」 を（正月休みの自由研究として）シミュレーション計算していました。非圧縮流体ソルバとDEMのソルバを組み合わせた連成解析ソルバを、（使いたてなので）かなりの試行錯誤＝時間を費やして、けれど「たった８行のC++コード」で書いて５分のCPUタイムを使って計算されていました。

　計算はグラスの断面右半分です。白い球は直径60μｍ（1mmの100分の6)の泡、ビールの粘度を10cP（水の10倍）としてみました。グラス中央では泡は浮力によって上向きに移動しますが、ガラス面では下向きに移動しています。ギネスは真っ黒で中央の泡の動きがみえないため、人間の目には泡が下向きに移動しているように見えます。

　以前、「ギネスビール風「下に沈む泡」を作るコツ」で紹介した、シミュレーションソフト FLUENT を使った「ギネスビールの泡は上がるか下がるか ?」では、「ギネスビールの下に沈む泡」の秘密をシミュレーション解析で解き明かしつつ、こんな風に書いています。

　古来, 人類は不可解な自然現象 に悩まされてきました. 由緒ある黒 ビール 「ギネス」 の泡がグラスの中 で下降しているように見えるのはな ぜだろう ? この現象は泡の物理的特 性に反するのでは ? ―― この単純 な疑問は, 何世紀もの間, 哲学者 や理論家達の論議の的となりながら も, 答えはみつからないままでした. しかし,数値流体力学 (CFD) により, 絶対的で信頼できる答えが導き出さ れました. 泡は上昇すると同時に下降していたのです.

　こんなカッコ良すぎる「いいセリフ」に書かれているような「何世紀もの謎を解き明かす作業」を、自分の意志で自由に使うことができる時間や道具の範囲で、つまりは「自由研究」でできる…って凄くいいな！と思います。

■続 「ギネスビールの下に沈む泡」をOpenFOAMで計算してみよう!?　

　ビール愛飲家が作成したグラス下部で発生した泡が、グラス内部でどう動くかを計算できるファイル群（参考：「ギネスビールの下に沈む泡」をOpenFOAMで計算してみよう!?）を使って、動粘度係数が違う時の「シュワシュワな炭酸泡の動き方・見え方」を計算してみました（設定値を私が１桁間違えている気もするのですが…）。

　左下から、炭酸飲料系モデルな粘度サラサラ系です。次の真ん中が、ギネスビールモデルで（グラスの外から見ると泡が下に落ちていく）ギネスカスケード発生系です。そして、最後の一番右が、粘度ドロドロな炭酸トマトジュース系（そんな飲料あったっけ？）。

　こうした解析作業を駆使して動粘度を最適化すれば、ギネスビール以上に華麗なギネスカスケードを魅せる至高・究極の黒ビール（もちろんグラス中央部の上昇泡が見えないような透過率や散乱率設定も必要でしょう）ができあがるかも！

■「高層ビルの風上・風下にある低層建物の壁近く」では「スカートをめくり上げてしまう風」が発生しやすい！？の法則　

　「都会でスカートがめくれやすい”改善すべき”キケンな場所を調べる」ために、つまり、「スカートをめくり上げてしまう風」が発生しやすい場所を探し出すために、流体計算フレームワークのOpenFoamで高層ビル周りの空気流を計算する tutorialを動かして、計算結果を眺めつつ考えます。…もしかしたら、「高層ビルの風上・風下にある低層建物の壁近く」では「スカートをめくり上げてしまう風」が発生しやすいのかもしれない！？

　　建物の配置と風向きの条件次第で大きく変わりそうですが、高層ビルの前後では地上から情報に吹き上げる風の流れが起きやすいような気もします。…といっても、それはあくまで「単にそんな気がする」というだけの理由です。

　大都会にそびえ立ついくつものビル近く、そういった場所を頻繁に歩く方も多いと思います。そういった経験ある方々に、「高層ビルの風上・風下にある低層建物の壁近く」では「スカートをめくり上げてしまう風」が発生しやすい！？の法則は果たして本当に成り立つものなのかどうか…それを訊いてみたい今日この頃です。