hirax.net::Keywords::「京都」のブログ

■一 乗寺と天下一品に代表される「裏の京都」　

　「京都の話である。Lispや非単調論理の業績によ って、Stanford大学のMcCarthy先生が、本年度 における、京セラ(もしくは稲盛財団)の京都賞 を受賞され、先日、京都国際会議場において、 その授与式が行われた。ということは、実は、 以下の話とは全く何の関係もない」という、凡才万歳の"みつを"チックなこんな話。

　東大は、どのような分野にせよ、日本を支えて 来たという自負があるから、学生も秀才であろ うとし、教官も秀才を秀才として世に出そうと する。一応、東大を出れば、大抵の学生は、そ れなりの企業などに入り、それなりの仕事をす る。

　これに対して、無秩序の京大は、天才か馬 鹿の二者択一を迫る。つまり、京大(特に理学部 にその傾向が顕著である)は、一握りの天才(そ のうちの何人かはノーベル賞などを受賞する)を 生み出すための大学であり、一握りの天才たち は、累々とした凡才たちの屍の上に立って世に 出るのである。

　京大の無秩序さは、どこかで見たり聞いたりし たような気がするに違いない。そう、阪神であ る。

■京都の街で「非ユークリッド幾何学」を体感しよう!?　

　京都市街は、基本的に道は東西に走るか、南北に走るかのいずれかです。たとえば、東西に走る「通り」は、丸太町通り・御池通り・三条通り・四条通り…といったものになりますし、南北に走る「通り」なら東大路・西大路・烏丸通り・堀川通り・河原町通り…といった具合になります。

　周辺部以外では、曲がりくねった道はなくて、道はすべて真っ直ぐ東<->西か南<->北方向に走っている。だから、どこに向かうにもただ、目的の方向に進み・曲がればいいだけだ。

「マンハッタン距離」と「続　理系風デート」

　マンハッタン距離を使うことができる街といえば、京都もそういう街のひとつです。東西南北方向に向けて、碁盤の目状に道が作られています。だから、太陽が真西に沈む春分と秋分の日近辺では、何本もの東西に走る道の向こうから夕日の光が差し込んでくる、ということになります。

春分と秋分の日には京都に行こう!?　

　だから、「南北という方向軸（＝道は東西に走る）」をX軸として、「東西という方向軸（＝道は南北に走る）」をY軸とすれば、すべての交差点はXY座標で示すことができることになります。だから、京都の交差点は「四条河原町(X=四条,Y=河原町)」とか「四条烏丸(X=四条,Y=烏丸)」とか「烏丸御池（X=御池,Y=烏丸）という具合に直行する２軸の座標値、すなわち通りの名前で表すことができ、その通りの名前を聞けば、どの場所に位置する交差点であるかが簡単にわかる、というわけです。XY座標で示される京都市街は、まさに「理系の散歩道」のために作られたような街、なのです。

　京都の街の凄いところは、小さな街なのに理系風散歩をすると、地球の曲率すら感じさせるところです。たとえば、烏丸御池から御池通りを「ひたすら真っ直ぐ」と西へ西へと進んでいくと、時代劇の撮影スタジオがあることでも有名な太秦近くに至ります。その太秦に辿り着く直前にある交差点が「三条御池」です。すなわち、東西に走る御池通りと三条通りが交差する交差点です。…何か「おかしくない？」「同じ方向に走るはずの”御池通りと三条通り”が交わることなんか不可能だよね？」と一瞬驚くわけです。

　けれど、理系の調味料がまぶされた頭の人ならば、こんな風に考えたりもするはずです。「そうか、オレは地球の上を移動していたんだよな。で、地球は丸いからは丸いんだから、そんな地表上の座標軸は２次元リーマン空間なんだから、その上では任意の２直線は実は必ず交わるわけだったな」「地球の丸さを考えれば、京都市街から離れれば、同じように東西に走る道同士が交差してしまうのもしょうがないな」「地球の曲率を意識してしまうくらい、太秦は京都中心からは遠い辺境の地だったんだな」…エトセトラエトセトラ。

　…もちろん、地球の曲率を感じさせるほどに京都の街が大きいわけでも、太秦が遠く離れた場所にあるわけではありません。いわゆる三条通りは、西大路通りのさら西を南北に走る「天神川通り（葛野中通り）」と交差した後に、道が進む方向を真西から西北方向へと変えてしまうのです。だから、三条通りの隣を平行に走り続けるはずの御池通りと交差することになり、「三条御池」という「本来ありえない名称を持つ交差点」が誕生してしまったというわけです。XY座標で示されるはずの空間の一部に、なぜかXX座標で表される場所が生じてしまったわけです。

　「理系の散歩道」を楽しむことができる人ならば、京都「三条御池」の交差点に行ってみると良いかもしれません。そこは小さな街のはずなのに地球の曲率をなぜか体感できるという、驚異のサイエンス・パワースポットなのです。

■交差点の位置を調べる「計算量」を京都の町で考える!?　

　京都の町では、多くの道が南北もしくは東西の方向に走っています。その結果、ほとんどの交差点は「直交する２つの道」により生まれ、そして、そんな交差点には「直交する２つの通りの名前を足された」名前が付けられるのです。

　だから、「南北という方向軸（＝道は東西に走る）」をX軸として、「東西という方向軸（＝道は南北に走る）」をY軸とすれば、すべての交差点はXY座標で示すことができることになります。だから、京都の交差点は「四条河原町(X=四条,Y=河原町)」とか「四条烏丸(X=四条,Y=烏丸)」とか「烏丸御池（X=御池,Y=烏丸）という具合に直行する２軸の座標値、すなわち通りの名前で表すことができ、その通りの名前を聞けば、どの場所に位置する交差点であるかが簡単にわかる、というわけです。XY座標で示される京都市街は、まさに「理系の散歩道」のために作られたような街、なのです。

京都の街で「非ユークリッド幾何学」を体感しよう!?

　もしもN本の東西の道と南北の道があるとしたら、交差点の総数はN^2ということになります。ということは、交差点の名称から場所を調べるための計算量は、O-記法で示すならO(N^2)もある、ということになります。これは、記憶力に問題がある私たちにはとても多すぎる量…です。

　ところが、いわゆる京都の街のような命名法を使っている場合には、つまり、「交差点の名称は、直交するふたつの通りの名称を結合することで作る」というルールにもとづくのであれば、東西・南北それぞれN本の通りの場所さえ覚えておけば、交差点名称から場所を調べるための計算量はたかだかO(2×N)≒O(N)にまで小さくなるのです。

　そんな計算量の削減・単純化ができるのは、「すべての道は直交する」という法則が、（「三条御池」というような特異点が生じることがない）京都中心街辺りではあるからです。

　交差点の信号機の下に掲げられた交差点の名称を長め、交差点の名称から場所を導き出すために必要な記憶量や計算量…そんなことを考え・楽しむことができるのが、「理系の散歩道」です。

　京都の街で、あなたの住む町で、「交差点の名称から場所を調べるための計算量」を考えてみることも楽しい」と思います。たとえば、あなたが知恵を絞れば、O(N^2)の計算が必要そうに思えるところをO(N log N)の計算量で済むようにすることができる…かもしれません。

■実は体育会系な 「京都市鴨川源流」を廻る「理系風デート」　

　今はカリーニングラードと呼ばれ、かつてはケーニヒスベルクという名前だったバルト海沿いにあるロシアの街を舞台にして、「流れる川により区切られた土地を、一筆書き状にすべて渡り、スタート地点に戻ってくることができるか？」という「謎かけ」が、「ケーニヒスベルクの橋渡りの問題」です。

　ケーニヒスベルクでなくとも、日常生活をする中で眺める街の景色の中にも、「ケーニヒスベルクの橋渡りの問題」は結構顔を出しているものです。たとえば、それは川崎の東京湾寄りのTOKIOのDASH海岸がある辺りに行けば、「ケーニヒスベルクの橋渡り問題」な案内看板を見かけることができます（街で見かけた「ケーニヒスベルクの橋渡り問題」）。そして、京都市街東部を流れる鴨川辺りにも、そんな「ケーニヒスベルクの橋渡り問題」があって、そこを巡る「理系風デート」が有名？であったりします（「京都市鴨川源流」を廻る「理系風デート」）。

　実際に鴨川辺りに行くと、「この橋渡り問題を解くべし」と、まさに「ケーニヒスベルクの橋渡り問題」な地図・看板がたくさん掲げられています。面白いことに、それぞれの地図ごとに川に渡された橋の数が異なっていて、つまり、地図ごとに「答え」が違うことに気づかされます。ある地図では、一筆書きが可能だけれども、ある地図では一筆書きをすることは不可能だということがわかったりするのです。…それを逆に言えば、地図ごとに答が違うからこそ、「ケーニヒスベルクの橋渡り問題」な地図を見つけるたびに、新しい問題（地図）を解く楽しみが生まれる、ということなのです。

　「一筆書きできる地図」を見つけ出し、一筆書きをしつつ川縁（かわべり）を回ってみても楽しいし、あるいは、川端（かわばた）にあるたくさんの「ケーニヒスベルクの橋渡り問題」な地図を眺め、それら「ケーニヒスベルクの橋渡り問題集」を解いて回るのも面白いものです。

　ところで、実際に「京都市鴨川源流」を廻る「理系風デート」をしてみると、結構長い距離を回らなければいけないことに気づきます。徒歩で歩き回るのはもちろん大変ですし、自転車で走り回るにしても、…やはり結構な時間ペダルを漕がなければなりません。また京都市街は南に比べて北の方が標高が高い、当たり前ですが、鴨川下流よりは上流の方が標高が高いわけですから、（目に見えないほどの斜度とはいえ）北上する時には坂を登る体力が必要です。

　たとえば上に貼り付けた地図のように、橋と橋の間の距離や、橋と橋の間の標高差が書かれている「ケーニヒスベルクの橋渡り問題」も見かけます。こんな問題（地図）を見かけたならば、「一筆書きをすることができるか」という問題だけでなく、「移動に必要な体力を最小化するにはどうしたら良いか」という（いわゆる）制約条件付き最小化問題を解いてみるのも興味深いかもしれません。…そして、その最小化問題を解いたなら、地図から解き明かした答えを確かめるべく、ひたすら鴨川の川縁（かわべり）を汗をかきつつ走り回るのです。

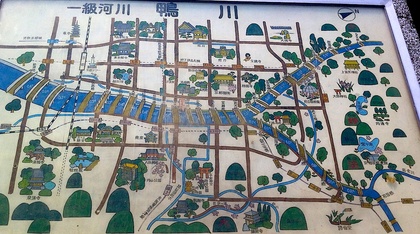
　「京都市鴨川源流」を廻る「理系風デート」は、実はとても体力を使う、実はかなり体育会系なデートです。少しだけ頭を使って考えたことを、体力と根性で確かめる、そんな楽しい「ケーニヒスベルクの橋渡り問題」なのです。

■「リッター20kmの燃費」な自転車ライフは「燃費が悪い」？　

　スラッシュドットの「自転車通勤は本当に一番エコな通勤形態かどうか調べてみた。」から。

　自転車を購入した段階で既に放出された 530 ポンドの温室効果ガスの元をとるのに自動車通勤をやめて自転車通勤をすることにした場合、自転車を漕ぐのにカロリーを燃焼することを考慮したとしてもアメリカ人の平均的な食事量を摂取しているならば 640 km 分の自転車走行で元が取れるという。往復 20 km の通勤であればおよそ一ヶ月半程度であろうか。

　今日は京都の街を自転車で走り回っていました。西は（担々麺屋を探して）山陰道樫原宿から東は（大津と京都の境界）山中越えの比叡山ドライブウェイ入り口まで、北は岩倉から南は（長岡京の西にある）ポンポン山まで…通算120kmちょっとです。6時間ほどの間に飲み食いした「エネルギー」は、500mlのペットボトルが10本くらいとガリガリ君が3本くらい、です。夏の日差しはとても熱く、30分にペットボトル一本くらいのペースで水分補給をし続けました。ガリガリ君は、冷たくシャキシャキする食感が絶品で（できれば梨ガリガリ君が食べたかったのですが、ソーダのガリガリ君しかなかったのが残念無念でした）、暑い夏を心地良くするための必需品です。

　…と、そんな一日の話をしていると、「燃費が悪いですねぇ。リッター20キロでは、ハイブリッドカーレベルです」という鋭く的確なツッコミを受けました。6時間で120kmということは１時間あたり20kmで、30分に500mlの飲料を一本飲んでいるということは…そう、ちょうど「リッター20kmの燃費」だったのです。そして、それでは「燃費が悪く」全然エコじゃない！というわけです。

　30分に一回の給油をし続け、しかも、その給油したガソリンは（汗として）ダダ漏れ状態です。…しかも、同じ飲み物ばかりを飲むのがイヤで…買う飲料を変えていった結果、途中から一本200円弱の「ハイオク給油」コースだったのです。ペットボトル500ml一本で200円ということは、ハイブリッドカーどころか、値段が高いハイオク燃料のさらに２倍のコスト…です。

　真夏の京都を縦横無尽に、エアコンをかけつつ自動車で120km走ったら、（さまざまな車があるでしょうが）平均としてはどのくらいのガソリンを消費するものでしょう？燃費が6リットルくらいで、トータル20リットルのガソリンを消費して、およそ3000円くらいでしょうか。車には何人も乗ることができることを考えれば、…真夏の「リッター20kmの燃費」な自転車ライフはあまりにも燃費が悪い、のかもしれません。