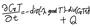hirax.net::Keywords::「反復計算」のブログ

トップページ"hirax.net" へ　/　サイトBlog "inside out" へ

「反復計算」に関する最新記事　/　「反復計算」に関する「説明」「記事の一覧」
より新しい5件の記事へ

2009-07-25[n年前へ]

■エクセルにおける循環参照時の計算順序　

　表計算ソフトのエクセルを使えるようになりたいと考えた。そこで、（これまで近づかないようにしていた）エクセルを使ってみることにした。まずは、エクセルの計算順序について調べてみた。もう少し具体的に書くと、計算の順番が「セル配置」に依存するのはどのような場合かを調べてみた。

　まず、最初にわかったのは「循環参照がない場合」には、（各セルの）計算順序は「セル配置」に依存しないということである（エクセルの計算プロセスの詳細）。また、「手動計算」や「反復計算」を行うようなオプション設定にしていたとしても、循環参照さえなければ（各セルの）計算順序は「セル配置」に依存しなかった。

　その一方で、循環参照があると、（各セルの）計算順序は「セル配置」に依存するようになる。具体的には、左上から横1行を計算したあと、その下の1行を計算し、さらにその下の1行を計算する…という具合である。

　だから、「反復計算」を1回だけ「手動計算」で行うような設定にし、
B1に2
A1に=B2
C1も=B2
B2は=B1
B1にA1-C1
という風に入力し、F9を押して手動計算させると、次々と値が変わり、6回周期の動きを示す。しかもA1とC1はいつも同じ値だが、その差分をとっているはずのB1は、ゼロになる瞬間もあるが、2とか-2とかゼロでない値にもなる。

　これは、循環参照が行われている場合に、反復計算オプションを付けた際の「各セルの計算順序」が前述のようだからである。当たり前の話のようだが、少し面白い。

この記事の「関連お勧め記事」を読む >>

2009-09-13[n年前へ]

■エクセルで「ランダム・ウォーク」アニメーション　

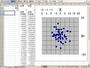
　「Excelでランダム・ウォークを計算させ、アニメーションさせる」と結構気持ちが良いものです。下の動画は、Excelで50個の粒子をランダム・ウォークさせている動画です。動画が始まって数秒した辺りから、計算が始まり、粒子がブルブル振動しながら拡散していきます。

この計算・グラフ表示は、（マクロ機能は使わずに）Excelの反復計算機能を用い、反復計算の回数は1回、計算タイミングは手動し、F9キーを押しっぱなしにすることで、行っています。Excelファイルは、RandomWalk.xls(35kB)としてダウンロードできるようにしてあるので、それで実際に試すことができるようになっています（反復計算の設定は上記通りにしておいてください）。

　計算の中身は、各粒子のX,Y座標を示すセルに対し、（単純に書くと）「自分のセル=自分のセル＋乱数(-0.5～0.5)」と入力してあるので、反復計算を1回するたびに、各セルの値が少しランダムに動いていく・・・という具合です。

　最左上のセルは、計算内容をリセットするためのフラグです。0を入力して、F9を一回押すと、計算内容がリセットされます。ランダムウォークの計算をする時には、この最左上セルに1を入力し、F9を押せば（押し続ければ）刻々と計算が実行され、グラフ上でランダムウォークのアニメーションを眺めることができます。最左上のセルの値を「各粒子のX,Y座標を示すセル」にかけているので、（反復計算を行った後でも）計算内容のリセットを行うことができる、というわけです。

　Excel作業につかれたとき、粒子たちに「ランダム・ウォーク」をさせ、プルプル震えながら動いていくようすを眺めてみると、何だか少し疲れがとれるかもしれません。

この記事の「関連お勧め記事」を読む >>

2009-12-07[n年前へ]

■エクセルの計算ワークシートをRuby計算スクリプトに変換してみよう　

　下記で使ったエクセルファイルは、自己参照部分がなく、つまり反復計算が必要ないものを使ってしまいました。反復収束計算が必要なエクセルファイルを「続　エクセルの計算ワークシートをRubyでC言語に変換してみよう」でサーバ内に置きましたので、下記記事を読んだ後には、上記記事（さらにその後に続く記事など）を引き続きご覧ください。

　目的に対して達成方法があまりに過剰、あるいは、あまりに的外れで荒唐無稽なものというのは、それはそれで何だか面白いような気がします。

　今日は、そんなものを、ふと、けれど無性に作ってみたくなりました。

　先日、Microsoft Excelのような「表計算ソフト」スプレッドシートを使った「静電界計算や非定常熱伝導シミュレーション計算」をみっちりしてきました。離散化された物理式を表計算ソフトウェアを用いて計算を行うというのは、「セル」というメッシュと空間が感覚的に近く感じられることから、とても自然にシミュレーション計算を行う空間分割と計算領域との対応を感じることができるのが、とても便利で良いと思っています。

　もちろん、セル間の計算を「反復計算」を行うことで、複雑なことを気にせず、計算が自然に終わってしまう、というのも実に「自然」で「お手軽」で良い、と思っています。

　とはいえ、私はエクセルは苦手です。毎年何回か、エクセルでのシミュレーション計算を（悩んでいる）人に教えるという作業をするのですが、それでもエクセルを使うのは苦手です。そこで、エクセルで作った離散化シミュレーション用.xlsシートをRuby Script（プログラム）に自動的に変換する、Rubyスクリプトを作ってみることにしました。そう、「エクセルで物理シミュレーションを学んだ人が、そのエクセルシートをそのまま多言語に移植することができる」スクリプトを作ってみよう、と考えてみたのです。

　作ったコードxls2rb.rbは次のようになります（近日中にサーバに置いて置きます）。これは、「反復計算を使った」エクセルファイルを読み込み、それをRubyスクリプトに変換するスクリプトです。「表計算ソフト」スプレッドシートを使いった「静電界計算や非定常熱伝導シミュレーション計算」は、四則演算と周囲の空間が持つ値の計算だけで行うことができます。だから、そういう「条件」下では、そんなスクリプトを作るのも比較的簡単です。初期化や反復計算をそれぞれ「関数」化しているとはいえ、変数はすべてグローバル変数ですし、そこら辺の「エクセル感」も再現してみたスクリプトです。

require 'win32ole'

def getAbsolutePath(filename)
  fso=WIN32OLE.new('Scripting.FileSystemObject')
  fso.GetAbsolutePathName(filename)
end

def getAlphabet(n)
  val=n.to_f/25.0 
  mod=n%25
  result=''
  result+=('a'..'z').to_a[(n-val)/25] if val>1
  result+=('a'..'z').to_a[mod]
end

def defFunc(state,book)
  src=''
  book.Worksheets.each do |sheet|
    y=1
    sheet.UsedRange.Rows.each do |row|
      x=0
      record=[]
      row.Columns.each do |cell|
        if state==:init &&cell.Value!=''
          record＜＜'  '+'$'+getAlphabet(x)+y.to_s+
            '='+cell.Value.to_s if cell.Value.to_s!=''
        end
        if state==:calc &&cell.Formula!=''
          t=cell.Formula.sub(/[=$]/,'')
          t=t.downcase.gsub(/([a-zA-Z]+\d+)/,'$\1')
          record＜＜'  '+'$'+getAlphabet(x)+y.to_s+'='+t
        end
        x+=1
      end
      src+=record.join("\n")+"\n" if record.join('').gsub("\n",'')!=''
      y+=1
    end
  end
  return src
end

filename=getAbsolutePath(ARGV[0])
excel=WIN32OLE.new('Excel.Application')
book=excel.Workbooks.Open(filename)
initsrc=defFunc(:init,book)
calcsrc=defFunc(:calc,book)
book.close
excel.quit
GC.start

puts ＜＜INIT
# autocreated ruby script from excel file
# jun hirabayashi jun@irax.net http://www.hirax.net

def init
#{initsrc}end

def calc
#{calcsrc}end

10.times do
  calc
end
INIT

　ちなみに、このスクリプトを

ruby xls2rb.rb ex.xls

という具合にして（引数は変換したいXLSファイルです）、実行すると、次のようなスクリプトができあがります。ちなみに、ここで使ったex.xlsファイルは、ラプラス方程式を3X3のセルに離散化し解く、実に単純なエクセルシートです。（この辺りのファイル一式を週末にでもサーバ上に置いておきます）

# autocreated ruby script from excel file
# jun hirabayashi jun@irax.net http://www.hirax.net

def init
  $a1=1.0
  $b1=2.0
  $c1=3.0
  $a2=1.0
  $b2=2.0
  $c2=5.0
  $a3=1.0
  $b3=2.0
  $c3=3.0
end

def calc
  $a1=1
  $b1=2
  $c1=3
  $a2=1
  $b2=2
  $c2=$b2+$c1
  $a3=1
  $b3=2
  $c3=3
end

10.times do
  calc
end

　つまり、今日私が作ったスクリプトの動作は、エクセルが最初に行う初期化ルーチンを"init"関数として定義（作成）し、次に行う反復計算を"calc"関数として定義（作成）し、それを（適当に決めた）10回繰り返すスクリプトを作り出す、という具合です。ポイントは初期化時には、cell.Valueを用いることで初期数値を設定し、逐次計算時にはcell.Formulaを使うことで数式を使う、という「使い分け」になります。反復計算自体は、ガウスザイデル法によって行われます。

　あとは適当に、知りたい値を出力する（たとえば、"puts $c2"といった）出力処理文でも書き足せば、はい、シミュレーション・rubyプログラムのできあがり、というわけです。

離散化された物理計算をするために作成したエクセル・シートを、Rubyスクリプトに自動で変換し、好きに加工できるプログラム…って便利なような、そもそもそんな用途ってある訳ないような…というのが正直で的確な感想だと思います。つまり、それはかなり無意味なツールです。

　他の言語に置き換えて、高速化指向の変換プログラムを書いてみるのも（一回くらいはやってみようと思いますが、今ひとつ「魅力」に欠けるように思います。

　今日作った、「離散化された物理現象を計算するために作成したエクセル・シートを、Rubyスクリプトに自動で変換するプログラム」なんていうものを、（何だか馬鹿馬鹿しいけれど）意外に少し面白い笑える、そう思える人が一人でもいたら、幸いに思います。

この記事の「関連お勧め記事」を読む >>

2009-12-10[n年前へ]

■エクセルでシミュレーション　Vol.8　二次元非定常熱伝導問題を解こう　

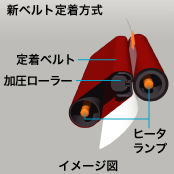
　表計算ソフト（スプレッドシート）プログラムであるMIcrosoft Excelを使い、（VBAはもちろん関数も使わず）ただセル間の加減乗除演算のみで、二次元非定常熱伝導問題を解きで遊んでみることにしてみました。伝熱方程式を差分化し、二次元の非定常解析を行ってみる、というものです。二次元といっても、比較的薄い円形ベルト（シート）上のものが回転するというモデルで、ベルト（シート）の厚みが（ベルト内の熱拡散に対して）十分に薄いという仮定の下での近似を行った、と考えれば、（そういう条件下の）三次元非定常熱伝導問題を解いているとも言えるシミュレーション計算モデルです。

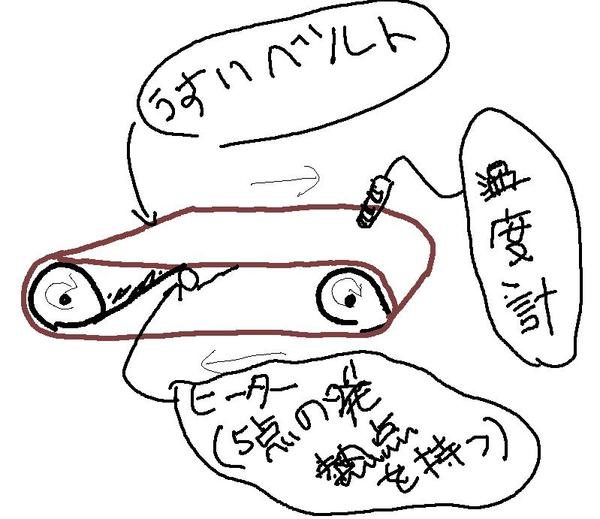　計算領域は右のようなものになり、2本のローラにより回転駆動させている「下から5点のヒータで温められている茶色のベルト」という計算するモデルです。その概略を大雑把に描いてみたのが、上図になります。

　というわけで、下の動画が、「ベルトが回転し動き」「途中にあるヒーターでベルトを温め」「ベルトの平面内では熱伝導が生じ」「周りの空気とベルトの境界から熱が放熱され」・・・といった2.2秒の間に生じることをすべて計算し・結果刻々と表示するシートで非定常伝熱計算を行っているようすです。（熱伝導率等はテキトーな値です）

ちなみに、このシートは、毎年行われている「スプレッドシートを用いた電子写真シミュレーション実習」テキストの「有限差分法による定着プロセスの熱伝導計算（非定常問題）」で使う教材用シート（関連テキスト）にもとづいています。

　動画の上の部分が、10×20の領域に差分化されたメッシュの温度分布を数値で示しており、動画の下部部分には温度分布をグラフで示しています。このグラフを眺めていれば、20℃の室温下で5点のヒータにより温度を上げられていく（回転する）ベルトが、次第に温度分布を持ちながらやがて定常的な温度分布になっていくさまを見てとることができます。

　この計算シートは、熱伝導方程式

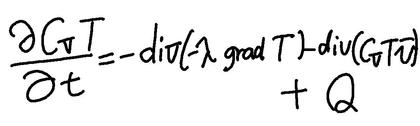
をCFL条件（Courant-Friedrichs-Lewy Condition)下で陽的に差分化し、エクセルの反復計算を用いることで、解いています。しかも、メッシュ間の計算は、ヤコビ法を用いた計算を行っています。

　「メッシュ間の計算は、ヤコビ法を用いた計算を行っている」と、ひとことで書きましたが、これは実は凄いことです。なぜかというと、エクセルは（セル間の循環参照がある場合に用いる）反復（収束）計算時には、表の左上をスタート地点として「Zの法則」の順序にしたがって（つまり、左上→右、そして一個下の行をまた左→右という順番で）逐次的に解くということをします。つまり、何も考えずにただ自分のセルの周囲との演算を行うと、「あるセルの計算を行うときには、自分の上と左のセルはすでに値が更新され新しい値が入っているが、右と下のセルはまだ古い値が入っている」という状態になります。つまり、ガウス・ザイデル法で計算されることになります（ヤコビ法は全セルの古い値を用いて計算を行った後に、全セルの値を新しい計算結果で置き換えますが、ガウス・ザイデル法は各メッシュ（セル・格子点）の計算を行ったら、その計算結果を、次のメッシュの計算時に即時に反映させて計算を行います）。

　定常問題を解くならガウスザイデル法で収束するまで反復計算を行うので構いませんが、非定常問題を解くのにガウスザイデル法を用いてしまうと、正確ではない間違った温度傾斜が生じてしまいます。それは、少し困ります（しかし、現在出版されている”表計算＋差分化　熱伝導”書籍は、多くがガウスザイデル法を用いています）。

　というわけで、この計算シートではグラフの下に（動画の）上のメッシュ部分をコピーするだけのセルがあり、上のメッシュ部分は「自分の周囲に相当する下のメッシュを用いてメッシュ間の計算を行う」という仕組みになっています。こうするとなぜ、ガウスザイデル法でなく、ヤコビ法の計算になるかは、「エクセルの反復計算時のセル間の計算順序」を念頭に置いて考えてみると、「なるほど！」と納得できると思います。「道具を理解し使いこなす」ということの意味を、心から実感させられます。

　だから、この二次元非定常熱伝導問題を解くエクセル・シートは、とても「単純明快な計算がされているだけ」なのですが、実に巧妙に考え抜かれた上で作られた「素晴らしき一品」です。しかも、セルを少しづつ書き変えていくことで、かなり実用的な計算もできるのです。このシートを見たときには、本当に驚かされました。

　「どんな風に書きかえると何がわかるか」とか「さらにこんなこともできる」といったことは、明日にでも書いてみようと思います。（というわけで、この続きとして、温度が時間を追って上昇していく機能も付けてみました）

この記事の「関連お勧め記事」を読む >>

2009-12-11[n年前へ]

■エクセルでシミュレーション　Vol.9　二次元非定常熱伝導問題の温度変化グラフも作ってみよう　

　この記事は、「エクセルでシミュレーション　Vol.8　二次元非定常熱伝導問題を解こう」の続きです。前回の記事では、比較的薄い円形ベルトが回転するモデルで、ベルトの厚みがベルト内の熱拡散に対して十分に薄いという仮定の下での近似を行ったと考えると）三次元非定常熱伝導問題を解いているとも言えなくない・・・というような二次元非定常熱伝導問題を解く、エクセルの表計算シートを作り眺めてみました。もちろん、VBAはもちろん関数も使わず、ただセル間の加減乗除演算のみで、熱伝導方程式を差分化したものです。

　今日は、計算領域の任意の部分の温度変化をグラフにする部分を前回のエクセルシートに追加してみようと思います。つまり、ベルト状に温度センサでも貼り付けたら、時々刻々と一体どんな温度が測定されるのかをシミュレーション計算時に表示させたい、というわけです。

　このような需要は非常に多くあると思いますが、一体それをどのようにすれば作ることができるでしょうか？エクセルのシート上は、非定常問題を解いているので、その瞬間その瞬間の温度分布しかデータが残っていないように思われ、スタート時からの温度変化をグラフにするのは難しいように思えてしまいます。

　しかし、「ガウスザイデル法でなく、ヤコビ法を用いて反復計算を行うために使ったテクニック」、すなわち、

　エクセルは（セル間の循環参照がある場合に用いる）反復（収束）計算時には、表の左上をスタート地点として「Zの法則」の順序にしたがって（つまり、左上→右、そして一個下の行をまた左→右という順番で）逐次的に解くという計算順序になります。

ということを利用すると、「計算領域の任意の部分の温度変化をグラフにする」ということが、いとも簡単に実現できてしまうのです。種明かしは後回しにして、まずはそのようなことをしているエクセルシート動画を下に張り付けてみます。動画の上部分は前回と同じく「回転するベルトを平面上の等高線色付きグラフとして表示したものです。そして、その下にあるのが、「等高線色付きグラフ右横部にある灰色円部分」の温度変化を横軸：時間・縦軸：温度で時系列グラフにしたものです。

　下の折れ線グラフを見れば、「等高線色付きグラフ右横部にある灰色円部分」の温度が時間を追って上昇していくようすをよく理解することができるのではないでしょうか。

　種明かしはこうです。エクセルのシートのずっと下方（下の行のセルに）"=温度変化を知りたいセル"という式を入れます。ここでいう温度変化を知りたいセルというのは、たとえば、X24といったセルを示す番号です。ですから、実際に（一番下のセルに）入れるのは、"=X24"といったものになります。

　そして、そのセルの上にあるセルをクリックし、=と入力した上で、その下のセルをクリックし"Enter"を押します。つまり、一個下の（さきほど"=X24"という式を入力した）セルを参照するようにするのです。そして、そのセルを選択した上で、上の方までズルズルズル～とコピーしてしまいます。

　エクセルの（セル間の循環参照がある場合に用いる）反復（収束）計算時の計算順序を考えてみれば、今「ズルズルズル～とコピー」を行った列には、「古い計算結果が上、一番下が最新の計算結果」という順序のデータが格納されていくことになります。（上から下に計算が逐次行われていることを考えると）計算ステップごとに、一個値が上に移動していくので、結果としてそのように時系列的なデータを保持できる、というわけです（結局のところ、ヤコビ法を用いるために、バッファエリアを下に設けたのと全く同じパターンです）。

　あとは、計算スタート時点からの（シミュレーション上の）経過時間なども同じように作り、散布折れ線図でも挿入すると、「上記のような「任意の部分の温度モニター機能付きの疑似三次元非定常熱伝導問題を解くエクセルシートのできあがり」となるわけです。もちろん、温度モニターは（上段で行ったことを他のセルに対してもしてやるだけで）いくつでも設置することができます。実に単純・簡単な（けれど巧妙な）実装ですがとても便利な機能です。

　さて、ベルトの温度モニター機能も付きましたので、今度はセンシングしたベルトの温度を用いて、ヒーターの温度を（まずは簡単なPID制御でも使って）制御しベルトの温度分布を適正に調節する機能例でも、簡単に実装し（ハードウェアをいじっている）気分にでも浸ってみることにしましょうか。

この記事の「関連お勧め記事」を読む >>

最新の「反復計算」に関する記事へより新しい5件の記事へ

>>「反復計算」に関する「説明」「記事の一覧」

■Powered by yagm.net

このページ上部へ

hirax.net::Keywords::「反復計算」のブログ

2009-07-25[n年前へ]

■エクセルにおける循環参照時の計算順序

2009-09-13[n年前へ]

■エクセルで「ランダム・ウォーク」アニメーション

2009-12-07[n年前へ]

■エクセルの計算ワークシートをRuby計算スクリプトに変換してみよう

2009-12-10[n年前へ]

■エクセルでシミュレーション Vol.8 二次元非定常熱伝導問題を解こう

2009-12-11[n年前へ]

■エクセルでシミュレーション Vol.9 二次元非定常熱伝導問題の温度変化グラフも作ってみよう

■エクセルにおける循環参照時の計算順序　

■エクセルで「ランダム・ウォーク」アニメーション　

■エクセルの計算ワークシートをRuby計算スクリプトに変換してみよう　

■エクセルでシミュレーション　Vol.8　二次元非定常熱伝導問題を解こう　

■エクセルでシミュレーション　Vol.9　二次元非定常熱伝導問題の温度変化グラフも作ってみよう　