2000-04-24[n年前へ]
■ボクのテレビは白黒だった 
Benhamのコマを作ってみよう
「O plus E」のバックナンバーを眺めていると面白い記事があった。1985/7のNo.68に畑田豊彦氏が書かれている「生理光学 -各種運動知覚現象 -」である。視覚周りの色々な話が書かれていた連載である。なぜ、こういう記事を読んでいるかというと、少し前の、
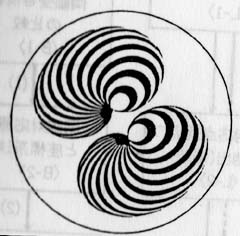
で視覚特性の資料を探した時に、この畑田豊彦氏の連載を見つけて以来、どうもはまってしまっていたのである。 特に今回面白く感じたのはBenhamのコマ(Benham's top)である。Benhamのコマというのは次のような画像を「コマ」にして回転させるというものだ。次に示すのは、「Oplus E」に掲載されていた杉浦康平氏デザインのBenhamのコマである。
 |
このような画像を回転させると、白黒の模様しか描かれていないのに、何故かほのかに色づいた模様が見える。それが、Benhamのコマである。人間の視覚特性のために、白黒模様から色を感じてしまうのである。こういった「おもちゃ」で子供の頃に遊んでいたように思うのだが、すっかり忘れていた。きっと、理科の時間などにこういった「おもちゃ」で遊んでいたはずなのに、記憶の彼方に飛んでしまっていた。こういう記事を読み返さないと、たぶん忘れたままになってしまっていただろう。
ところで、プリンターをお持ちの方は、このWEBページを印刷して、コマを作成してみると面白いと思う。白黒プリンターで印刷しても、コマさえ作れば、アラ不思議、その回転するコマは色づいて見えるのである。モノクロプリンターでもカラー模様が印刷できるわけだ(人間が感じるところまで含めれば)。
他にも「O plus E」に掲載されていた杉浦康平氏デザインのBenhamのコマを示しておく。
 |
さて、このBenhamのコマを私も作成してみようと思う。もちろん、実際にコマは作成して楽しんでみたのだ。しかし、せっかくなので、動画ファイルの形で簡単に見ることができるようにしてみた。WEB上で簡単に見ることができるBenhamのコマである。
先の、「杉浦康平氏デザインのBenhamのコマ その1」を回転させるのではなく、時間的に変化する動画にしてみるのだ。といっても、こう書いただけでは判りにくいので、図で示してみる。まずは、作成した動画の各「コマ(このコマは静止画の意味)」を見てみよう。
 |  |  |
 |  |  |
これが、「杉浦康平氏デザインのBenhamのコマ その1」を時間的に変化する動画にしてみたものだ。この図で4,5,6コマめが、先のA,B, Cに対応しているわけである。
これをある程度高速で連続的に眺めると、この白黒模様が色づいて見えるはずである。まずは、これらの画像をアニメーションGIF画像にしたものを次に示す。とはいっても、作っては見たが再生スピードがどうにも遅い。これでは、色づいて見えるどころではない。このBenhamのコマをアニメーションGIFにする計画はひとまず挫折である。
 |
そこで、先の画像をAVIファイルにまとめたものを作ってみた。こちらの方ならスピードはなんとか満足できている(少なくとも、私の環境では)。AVIファイルということで、Windows以外の環境では不便だと思うが、動画変化ツールは色々あるから大丈夫だろう(多分)。
人によって、どの速さの場合が一番色づいて見えるかどうかは異なるだろうから、三種類の速度のものを作成してみた。それをここにおいておく。ちなみに、再生ソフトの設定を「自動繰り返し」にする必要がある。
さて、WEB上で情報を探してみると、面白い話があった。
- 色あそびコマ (http://www.avis.ne.jp/~g-k-toys/sakuhin.4.html )
昔、ウルトラマンをTVで見ていた頃、白黒TVで見ていた。その頃は、カラータイマーの色は私にはよく判らなかった。ボクのテレビは白黒だったからだ。ウルトラマンのカラータイマーの点滅をこのBenhamのコマのパターンで放送したりしたら、とても面白かったのにな、と思うのである。
2003-03-27[n年前へ]
■「視覚特性を考慮したイメージング技術」 
4月18日(金)13:00 - 19:00 at 東工大の「視覚特性を考慮したイメージング技術」に行くんですが、これに行きますか?と誰にともなく聞いてみる。
2003-06-10[n年前へ]
■アナタのココロの中にだけ 
音楽が素敵なFLAH。適当に名付けてしまえば、アナタのココロの中にだけ。これは結構有名な「視覚特性を使った面白い画像」ですね。ココロの綺麗な人には何かが見えるというわけですけれど、もちろん誰でも見えます。もちろん、誰でもココロが綺麗なわけですね。
2006-02-12[n年前へ]
■斜め配置CCD・CMOの秘密 前編 
「画素を45度回転させ斜めに配置した」クリアビッドCMOSセンサをSONYが発表した時に、Fast & First 情報掲示板(No.9601, No.9603)で「斜め配置センサと通常配置センサの解像度」について少し書かれています。それを面白く読みながら、書かれていたことを自分なりに整理して、つらつらと考えごとをしてみました。その内容を前編・中編・後編としてまとめてみることにします。あくまで撮像素子の部分だけを考え、後の画像処理の部分については全く考えていません。また、素人のテキトーな自主学習なので、内容について信頼性が全然ないことをお断りしておきます。
撮像素子を45度傾けると高解像度に
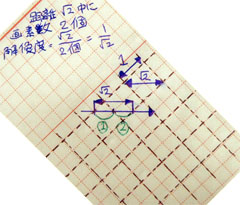
 通常の撮像素子の画素は垂直・水平方向に綺麗に並んでいます。例えば、撮像素子の画素を適当に描いてみると右のような感じになります。つまり、単位長さ1×1の大きさの正方形状画素が(各画素が垂直・水平方向に並びながら)平面をびっしり埋めている、というイメージです。こんなイメージ画像を描いてみた後に、水平(あるいは垂直)方向の解像度、すなわち「単位長さあたりの画素数」がどうなるかを考えてみることにします。
通常の撮像素子の画素は垂直・水平方向に綺麗に並んでいます。例えば、撮像素子の画素を適当に描いてみると右のような感じになります。つまり、単位長さ1×1の大きさの正方形状画素が(各画素が垂直・水平方向に並びながら)平面をびっしり埋めている、というイメージです。こんなイメージ画像を描いてみた後に、水平(あるいは垂直)方向の解像度、すなわち「単位長さあたりの画素数」がどうなるかを考えてみることにします。
この場合、画素の大きさが1なのですから、距離(単位長)1あたり画素が1個あることはすぐにわかります。つまり、水平(垂直)方向の解像度は「単位長さ辺り1画素」となっているわけです。試しに、水平(垂直)線を任意の場所で描いてみると、「長さ1あたり画素を必ず1個横切る(長さ1あたり画素が1個ある)」ということを確認することができます。
 それでは、この撮像素子中の画素配置を45度傾けた(回転させた)場合、水平(垂直)方向の解像度はどのようになるでしょうか? この場合も、適当なイメージ画像を描いて考えてみることにしましょう。…そこで、右のように、各画素の配置を「45度」回転させた撮像素子を描いてみます。そして、水平(垂直)線を任意の場所で描いてみると、「ほぼ(つまりごく限られた特殊な条件を除き)」全ての箇所で「長さ√2あたり画素を必ず2個横切る(長さ√2あたり画素が2個ある)」ことがわかります。
それでは、この撮像素子中の画素配置を45度傾けた(回転させた)場合、水平(垂直)方向の解像度はどのようになるでしょうか? この場合も、適当なイメージ画像を描いて考えてみることにしましょう。…そこで、右のように、各画素の配置を「45度」回転させた撮像素子を描いてみます。そして、水平(垂直)線を任意の場所で描いてみると、「ほぼ(つまりごく限られた特殊な条件を除き)」全ての箇所で「長さ√2あたり画素を必ず2個横切る(長さ√2あたり画素が2個ある)」ことがわかります。
つまり、水平(垂直)方向に対しては、単位長あたり「2 / √ 2 = √ 2 ≒ 1.4」個の画素があることになるのです。つまり、撮像素子の画素を45度斜めに傾いた配置にすることで、1.4倍の解像度化を実現することができた、ということになります。もちろん、(この状態で)45度斜めの方向に対する解像度は「単位長1あたり1個の画素」ということになっているわけですから、逆に言えば、水平・垂直方向に各画素が綺麗に並んでいる配置の場合には、45度斜めの方向に対する解像度が「水平・垂直方向よりも1.4倍高かった」ということになるわけです。
視覚特性は斜め方向には鈍い
ところで、人間の視覚特性は斜め方向に対しては感覚が鈍くなっています。ということは、人間が画像を眺める際には、その画像の斜め方向の解像度は低くても構わない、ということになります。斜め方向の解像度は低くても構わないから、その分水平・垂直方向の解像度が高い方が良い(アラが目立たない)というわけです。つまり、「ごくごく単純に考える限りは」画素配置を45度斜めに傾けたタイプの撮像素子の方が、人間の視覚特性と特性が合っていて都合が良い、という風に思えます。
それでは、現在多く発売されている製品で使われている撮像素子を45度傾ければ高解像度化するか、というとそうはなりません。それは、現状の撮像素子では(本来モノクロの)撮像素子をカラー化する時の手順中において、(多くの場合)すでに45度回転のテクニックが使われているからです。
RGGBフィルタを使ったカラー化の場合
 本来「カラー」でない撮像素子をカラー化するためには、色のついたフィルタを撮像素子の前にとりつけることになります。例えば、原色フィルタと呼ばれる「赤・緑・青色のカラーフィルタなどを各画素の前にとりつけるシステム」では、赤色・緑色・青色それぞれの光の割合がわかるように、各画素の前にRGB(Red, Green, Blue)いずれかの色のフィルタをつけます。例えば、右のイメージ図はRGGB配列のベイヤー配列のカラーフィルタのイメージ図です。近隣4画素のうち、1画素ずつに青色と赤色のフィルタを張り、残り2画素に緑色のフィルタが張られています。緑色の画素が青色と赤色の画素の2倍の量にされているのは、人間が感じる視覚特性は緑色の成分によるところが大きいからです。
本来「カラー」でない撮像素子をカラー化するためには、色のついたフィルタを撮像素子の前にとりつけることになります。例えば、原色フィルタと呼ばれる「赤・緑・青色のカラーフィルタなどを各画素の前にとりつけるシステム」では、赤色・緑色・青色それぞれの光の割合がわかるように、各画素の前にRGB(Red, Green, Blue)いずれかの色のフィルタをつけます。例えば、右のイメージ図はRGGB配列のベイヤー配列のカラーフィルタのイメージ図です。近隣4画素のうち、1画素ずつに青色と赤色のフィルタを張り、残り2画素に緑色のフィルタが張られています。緑色の画素が青色と赤色の画素の2倍の量にされているのは、人間が感じる視覚特性は緑色の成分によるところが大きいからです。
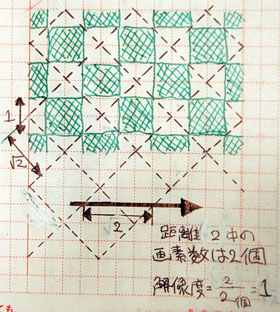 それでは、話を簡単にするために、人間が感じる視覚特性への寄与が大きい緑色に割り当てられた画素だけを抽出して、フィルタ方式のカラー撮像素子における解像度を考えてみることにします。右の画像は、緑色の画素だけを描き、そして各画素間の境界線中心を点線で描いてみたものです。このように、補助線を描いてみると、緑色を担う各画素がどのように配置しているかがわかりやすくイメージできるようになります。この点線で描かれた緑色の画素配置をひとことで大雑把に言ってしまえば、√2×√2の大きさの画素が45度傾いた状態で配置されている、ということになります。つまり、つまり、RGGB型のベイヤー配列のカラーフィルタを使ったカラー撮像素子においては、すでに45度回転配置により高解像度化のテクニックが(視覚特性への寄与が大きい緑色に対して)使われているというわけです。
それでは、話を簡単にするために、人間が感じる視覚特性への寄与が大きい緑色に割り当てられた画素だけを抽出して、フィルタ方式のカラー撮像素子における解像度を考えてみることにします。右の画像は、緑色の画素だけを描き、そして各画素間の境界線中心を点線で描いてみたものです。このように、補助線を描いてみると、緑色を担う各画素がどのように配置しているかがわかりやすくイメージできるようになります。この点線で描かれた緑色の画素配置をひとことで大雑把に言ってしまえば、√2×√2の大きさの画素が45度傾いた状態で配置されている、ということになります。つまり、つまり、RGGB型のベイヤー配列のカラーフィルタを使ったカラー撮像素子においては、すでに45度回転配置により高解像度化のテクニックが(視覚特性への寄与が大きい緑色に対して)使われているというわけです。
実際、右の画像で、水平(垂直)線を任意の場所で描いてみれば、「ほぼ(つまりごく限られた特殊な条件を除き)」全ての箇所で「長さ2あたり画素を必ず2個横切る(長さ2あたり画素が2個ある)」ことがわかります。つまり、単位長さ1に対して水平(垂直)方向には画素が1個の解像度がある、というわけです。本来は「√2×√2の大きさの画素」ですから、もしも45度回転したような配置にしなければ、水平(垂直)方向には長さ√2あたり1画素の解像度しかなかった、ということになります。しかし、緑色が斜めに配置されたRGGB配置にすることで、緑色画素を45度回転させることができて、結果として1.4倍の高解像度化がされていることになります。
RGGBフィルタCCDを45度回転させたらどうなる…?
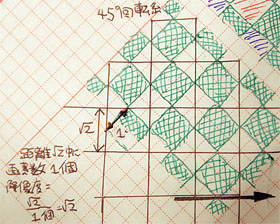 それでは、カラーフィルタがRGGBの配置をしている撮像素子を45度回転させた場合にはどのようなことが起きるのでしょうか? 例えば、右の画像のように回転・配置させてみた場合には、解像度はどのようになるのでしょうか。右の配置は、ちょうど冨士フィルムのハニカムCCD(資料1資料2)と同じような場合なのですが、この場合に人間の視覚特性上重要な水平・垂直方向の解像度はどのようになっているのでしょうか? …上の例と同じように、このRGGBフィルタCCDを45度回転させた場合でも考えてみることにしましょう。
それでは、カラーフィルタがRGGBの配置をしている撮像素子を45度回転させた場合にはどのようなことが起きるのでしょうか? 例えば、右の画像のように回転・配置させてみた場合には、解像度はどのようになるのでしょうか。右の配置は、ちょうど冨士フィルムのハニカムCCD(資料1資料2)と同じような場合なのですが、この場合に人間の視覚特性上重要な水平・垂直方向の解像度はどのようになっているのでしょうか? …上の例と同じように、このRGGBフィルタCCDを45度回転させた場合でも考えてみることにしましょう。
さきほどと同じく、この右の画像には緑色の画素だけを描いてあり、そして各画素間の境界線中心を示す直線を描いてあります。すると、この場合というのは、「√2×√2の大きさの画素」が水平垂直方向に綺麗に並んでいることがわかります。そして、この画像中で水平(垂直)線を任意の場所で描いてみれば、全ての箇所で「長さ√2あたり画素を必ず1個横切る(長さ√2あたり画素が1個ある)」ことがわかります。長さ√2あたり画素が1個ということは、単位長さ1あたりならば水平(垂直)方向に画素が0.7個の解像度ということになります。
つまり、RGGBフィルタCCDを45度回転させてしまうと、視覚特性上重要な緑色の水平・垂直方向の解像度が「単位長あたり1画素」から「単位長あたり0.7画素」に低下してしまっている、ということになります。ということは、単純に「人間にとって重要な緑色の解像度」だけを考えるのであれば、(RGGBフィルタを使った場合)斜め配置センサは決して有利とはいえない、ということがわかります。
クリアビッドCMOSセンサの場合
 単純に「人間にとって重要な緑色の解像度」だけを考えるのであれば、(RGGBフィルタを使った場合)斜め配置センサは決して有利とはいえないというのであれば、先日発表されたクリアビッドCMOSセンサの場合には一体どうなっているのでしょうか…?謳い文句の「画素を45度回転させ斜めに配置することで、1画素の面積を大きくしながら(高感度にしながら)、解像度は維持」というものは一体どういうことなのでしょうか?
単純に「人間にとって重要な緑色の解像度」だけを考えるのであれば、(RGGBフィルタを使った場合)斜め配置センサは決して有利とはいえないというのであれば、先日発表されたクリアビッドCMOSセンサの場合には一体どうなっているのでしょうか…?謳い文句の「画素を45度回転させ斜めに配置することで、1画素の面積を大きくしながら(高感度にしながら)、解像度は維持」というものは一体どういうことなのでしょうか?
そこで、SONYのサイトにある情報(右にページ・サムネイルで示したページ)を見てみると、RGGB配置のカラーフィルタを使っているわけではないことがわかります。4画素×4画素中に緑色を12画素を配置し・赤色と青色を2画素ずつ配置するという独自の配列です。つまり、大胆に言ってしまえば、ほとんどの画素を緑色担当にしているわけです。よくあるカラーフィルタの配置とは全く違うわけです。
ほとんどの画素が緑色担当ということは、非常に大雑把に言ってしまえば、緑色単色のモノクロ撮像素子のようなものですから、一番最初に「撮像素子を45度傾けると高解像度に」で書いたように、45度回転配置による高解像度化の効果が生じます。クリアビッドCMOSセンサの場合、1画素の面積を大きくすることで高感度を実現しようとしています。つまり、通常であれば1×1の大きさの画素の面積を大きくして、√2×√2の大きさにしてあります。そして、その画素を斜め45度に回転させたモノクロ撮像素子のようなものであるわけです。…ということは、結局のところ、上で考えてみた「RGGBフィルタを使ったカラー撮像素子」と全く同じ解像度であることがわかります。なるほど、赤色と青色の画素数を減らし、その分の面積を緑色に回すことで、高感度と高解像度を両立させようという考え方であるようです。
色情報の解像度はどうなる?ハニカムCCDなら…?
ところで、クリアビッドCMOSセンサの場合には、赤色と青色の画素数を減らしているわけですから、色情報の解像度をある程度低く設定しているわけです。また、「RGGB配置を45度回転させた」富士フィルムのハニカムCCDは(視覚特性上重要な)緑色に関する限り解像度の点で有利には見えないわけですが、やはり何らかのメリットはあるはずです。そこで、そういった点について、中編・後編で考えてみたいと思います。
2007-04-28[n年前へ]
■Spectrum Color Conversion 

CMY<=>RGB の色変換の際に用いている基準は、「スペクトル強度の差の自乗和が最小になること」です。つまり、人の視覚特性などに特化した色変換ではなく、単純に分光強度の形状が近くなるような色変換を行っています。また、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルは非常に大雑把な値を使っています。特に、シアン・マゼンダ・イエローに関しては、印刷で用いられているインクとは異なり、比較的理想に近い吸収スペクトルの場合を示しています。もしも、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルを眺めてみたい場合には、RGBtoCMYやCMYtoRGBの入力値として、単色だけを255にして、それ以外の色を0にしてみて下さい。たとえばシアンだけがある場合の単色スペクトルを眺めたければ、シアン=255, マゼンダ=0、イエロー=0にする、という具合です。すると、その色だけを使った時のスペクトルを見ることができるわけです。ただし、減産混色の場合に表示されるのは、いわゆる吸収スペクトルではなく、インクに吸収されなかったスペクトルということになります。また、CMYが示している量には対数変換がかけられています。
RGBtoCMYとCMYtoRGBは、相互に入力スペクトルと再現されたスペクトルを比較することもできますから、RGBとCMYの間で相互に色変換を繰り返しながらスペクトルの変化を眺めてみるのも面白いかもしれません。
なお、このSpectrum Color Conversion は、離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージをWolfram Technology 社のMathematica上で作成し、webMathematica エンジンを用いることで、web アプリケーションとして動作しています。