hirax.net::Keywords::「加熱」のブログ

■加熱用の点滴と生食用の点滴　

　ゴールデンウィークに続き、またしても疲れが溜まり、扁桃腺が腫れて高い熱が出た。病院に行き、一時間ほど点滴を受けながら、点滴の液体が入っている袋をぼんやり眺めていると、「生食」と大きく書いてある。「そうか、点滴は生(なま)で食べる人がいるのか」「味は結構美味しいのかな？」「あれ…？生食ってことは、点滴を(生食とは逆に)加熱して食べたり飲んだりする人がいるのか…？」と数分考えてしまった。もちろん、点滴に使っている「生理食塩液」を略して「生食」であるわけで、ホタテじゃあるまいし、点滴に「加熱用」「生食用」だなんてあるわけがない。そんな間抜けなことを考えていたのは、全て発熱のせいだ…と思いたい今日この頃。

■PSoC制御の「加熱ホッケーブレード」や「堅さ可変シューズ」　

　PSoCはCypress社のマイコン・チップで、各種デジタル・アナログ回路が搭載されていて、その組み合わせをユーザがプログラミング（設計）できる、というものだ。FPGAほど高性能ではないけれど、PICより少し賢く便利なアナログ回路が色々詰めあわされている（だから周辺回路を大幅に減らすことができる）、という感じだろうか。アナログ制御・入出力をしたい場合には、とても便利そうなチップである。

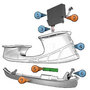
　このPSoCが使われている商品で面白いなぁ、と思うのが「Therma Blade」と「adidas_1, intelligence level 1.1.」だ。

　一方、adidas_1, intelligence level 1.1.の方は、PSoCで制御したモータで踵部分にあるエアクッション部を押すことで、エアクッション内圧力＝靴の堅さ（衝撃吸収率）を適正に変える、というものだ。電子制御されている車のサスペンション機構（タイヤと車ボディの間で、路面の凹凸・カーブなどがあるときの衝撃を吸収する機構）も多いけれど、それと同じような技術が搭載されたシューズである。

　こういったシューズで高機能・高付加価値の流れはどれだけ進んでいくのだろうか。いつか、「トランジスタ技術４月号」で、「フレッシャーズのためのアイスホッケーシューズ制御のABC」といった特集記事が当たり前のように書かれる日が来るのだろうか。

■エクセルでシミュレーション Vol.6 「夏にフライパンで卵焼き 編」　

　「表計算ソフトウェアでシミュレーションをする」という講習を見続け、何よりも面白かったのが「非定常の３次元熱計算を簡単に、それでいて、できる限りきちんと計算をやってみよう」という（I氏が講師の）シリーズです。

　一次元非定常の熱拡散問題を陰的解法で解く「熱伝導方程式を表計算ソフトで解くサンプル」は多いように思いますが、「非定常の３次元熱計算を表計算ソフトウェアで解く簡単にやるテクニック・サンプル」は、（私は）他では見たことがありません。しかも、このシリーズは本当に簡単で、なおかつ、できる限り精度を保証して解く、というとても稀有な例です。「難しい問題」を「簡単に」「きちんと」「精度を保証して」解く…といったようなものたちは相反することが多いわけですから、そういったものを兼ね備えているというのは、とても珍しいと思うわけです。

　下の例は、そのテキストを利用して、陽的解法で安定性条件が成り立つようにして、「夏の朝に、角型フライパンをコンロで加熱した際のフライパン温度分布」を計算した例になります。ある厚みを持ったフライパンが、コンロのガスの炎が当たっている部分が「100度」に（熱）されているような条件の時、フライパンの温度分布が時々刻々と変わっていくようすを計算した結果です。こんな計算をエクセルで数回しておけば、「美味しい卵焼きを作るための最適条件・最適なやり方」を導き出すことだってできるかも、と思わされるのです。エクセル上で、フライパンの厚みや熱伝導度を変え、コンロの炎分布を色々変えてみたりしたならば、究極・至高の卵焼きを作るための最適・必須条件が見つかるかもしれない、と楽しく思えてきたりします。

　ところで、この「非定常３次元熱計算」のエクセルシートは、本当に簡単に作ることができるのですが、その一方で、このシートは（簡単なのに）実に巧みに作られています。だからこそ、「難しい問題」を「簡単に」「きちんと」「精度を保証して」解くことができるわけです。

　その「巧みさ」を紐解いてみると、これが実に綺麗なパズルのようで、とても面白いのです。・・・というわけで、その「巧みさ」「面白さ」についての感想文は、また後ほど書いてみようと思います。