2000-03-12[n年前へ]
■元気な私とカゼひく私 
ガラガラ声の秘密
のどが痛いし、微熱がある。どうやら、扁桃腺が腫れているらしい。「あー」と言おうとすると、「あ”ー」という声になってしまう。まさにガラガラ声である。
ところで、ガラガラ声というのは一体どういう声なのだろう。もちろん、私の今の「あ”ー」という声はガラガラ声なのはわかる。しかし、このガラガラ声の特性をちゃんと定量化すべきだろう、と思うのである。まずは可能な限り、考えたり定量化したりしなければならないだろう。「感覚的なもの」というのは、そういうことをした後に持ち出すべきである。(考えること無しに)感覚的に判ったつもりになっているのは、何も感じていないのと同じである。それは、「想像力の欠如」に至ってしまうと思う。そして、想像力の欠如は「その人の地平線」を狭く(狭いという表現はおかしいようにも思うが)してしまう。何かワケの分からない文章だと感じるようであれば、それは私の頭が熱でふらふらになっているせいである。
さて、
で私の「アイウエオ」の声についての解析を行った。今回も、同じように私の「アイウエオ」の声について調べてみたいと思う。そうすれば、過去の「元気な私」と現在の「カゼひく私」の声の違いがわかるかもしれない。そして、ガラガラ声とは一体何なのか?ということの手がかりが掴めるかもしれない。 まずは、前回と同じように - F1-F2空間における私の「アイウエオ」 - を調べてみる。カゼをひいてガラガラ声になることで、私の「アイウエオ」のフォルマントはどう変化しただろうか?次の図がF1-F2空間における「元気な私のアイウエオ(●)と扁桃腺が腫れている私のアイウエオ(●)」を示したものである。
 |
面白いことに、前回標準的な分布から外れていた私の「ア、オ」が今回は標準分布の中に収まっている。ガラガラ声になることで、私はやっと標準的な「アイウエオ」になるようである。何故だか、よくわからないが、面白い。まぁ、きっとフォルマント判断の際のピーク検出精度の問題だとは思うのであるが、不思議な結果である。
それでは、この「アイウエオ」の変化は一体どのようなものだろうか?音声波形を見てみることにする。それが次に示す図である。
まずは、「あ」の波形である。
元気な私  扁桃腺が腫れている私  |
元気な私の「あ」が割に単純な正弦波に近い。ただし、完全に上下対称な正弦波ではなくて、上に凸な部分の方が若干立ち上がりが速い波形のように見える。そして、割に綺麗に同じ波形が繰り返されている。
それに対して、扁桃腺が腫れている私の「あ」はスパイクノイズの入っている波形になってしまっている。こちらもスパイクノイズの入り方は割に同じ繰り返しである。
また、元気な頃の私の「あ」がF1-F2空間における標準的な「あ」分布と離れていたのは、F2が弱いせいではないかという予想ができるのではないだろうか?本来、上下の立ち上がりが異なるのが普通であるが、私の「あ」は上下が比較的同じであり、それでフォルマント判断の際のピーク検出精度が低下していたのではないか、という考えである。
それに対して、扁桃腺が腫れている私の「あ」は上下の立ち上がりがかなり異なり、周波数ピーク検出が容易であったのではないか、と私は考えるのである。
さて、次は「い」である。
元気な私  扁桃腺が腫れている私  |
これもやはり、基本的には同じ波形であることはわかる。しかし、元気な時には上に尖っている部分が、扁桃腺が腫れている私の「い」ではまるで部分的に上下逆転しているかのようになってしまっている。まるで、周波数毎の位相特性が異なっているアンプやスピーカーのようである。
次が「う」である。ここまでくると、同じ「う」に聞こえるのが不思議なくらいである。
元気な私  扁桃腺が腫れている私  |
見た目には、完全に別物の波形に見えてしまう。しかし、フォルマント上は「元気な私」と「扁桃腺が腫れている私」でほぼ同じ(F1-F2空間における私の「アイウエオ」を参照)であることを考えると、
- 各周波数の位相がずれている
- 高周波が重畳されている
次の「え」も「う」と同じ傾向である。フォルマント上は同じというのが、目で見る限りはよくわからない。いや、もしかしたら見慣れたらわかるようになるのかもしれないが、今の私の心の目ではよくわからないのである。
元気な私  扁桃腺が腫れている私 元気な私  |
最後の、「お」はもう何が何だかわからない。しいて言うならば、元気な私の「お」は高周波が極めて多いが、扁桃腺が腫れている私の「お」は高周波はあまりない。きっと、扁桃腺が腫れている私のノドの応答特性が低下しているせいだろう。しかし、これまでのスパイクノイズが増えている事実とどう繋がるかは、難しいところである。うーん、違うかもしれない…
元気な私  扁桃腺が腫れている私  |
ここまでは音声波形を見てきたが、最後に周波数空間での違いを示してみる。元気な私のアイウエオに比べて、扁桃腺が腫れている私のアイウエオは割に高周波が増えていることがわかる。やはり、先の「お」の考察は違っているのかもしれない。
 |  |
扁桃腺が腫れている私の声の周波数が高い辺りにいくつも見えるピークは私の「のどの痛みの証し」である。あ”ー、しんどい。いや、ホントにしんどいのである。
さて、私は鈴が鳴るような綺麗な声がとても好きなのである。いつか、そういう声の秘密について調べてみたい、と思うのであった。また、色々な歌手の声のスペクトログラムについても調べてみたい、と思う。
2000-10-15[n年前へ]
■地平線際の星が見える場所 
「地平線近くの月が大きく見えるのが、比較対象物があるせいならば、何故地平線際の星座は大きく見えないのか」というメールに返事を書く。星座だって本当は大きく見えたりしているのだけれど、気にしたことがなかったり、地平線際の星が見えなかったりするだけではないでしょうか、と書いた。月に比べて普通の星はずっと暗いので、街の中のビルなんかの明かりの近くにあるときっとはっきりと見ることはできないだろう。私がかつて住んでいた長野県の野辺山でも今では山際にスキー場がいくつかあるし、ライトアップされた45m電波望遠鏡もある。きっと、もうあそこでも山際で光る星は見えづらいのだろう。
2001-07-25[n年前へ]
■遠い空のはて? 
地平線の向こうに手を伸ばせ
先日、富士山の五合目へ行った。と一言で言っても、富士山の五合目にも色々ある。何しろ上り口が、第一人気の「吉田口・河口湖口」、下りの「砂走り」で有名な「御殿場口」「須走口」、そして測候所の白ドームを目指し最短距離一直線の「富士宮口」と四種類もあるのだ。その色々ある五合目の中で、先日私が行ったのは富士宮口の五合目というところだ。富士山の太平洋側から富士山頂に向かう登山口の標高2400m地点ということになる。もしかしたら、表富士五合目と言う言い方のほうが有名なのかもしれない。
その表富士五合目から下を眺めると、ずいぶんと遠くまで見えることに本当に心からビックリした。雲が下のほうに広がっていて、そしてその向こうに海や山や地平線が見える。そして、気のせいか地平線がとても丸いような気がする。その五合目までは車で簡単に来ることができたのだけれど、さすが標高2400mは伊達ではなかった…。やっぱり富士山は日本一の山かもしれない…。そして、そんな景色を眺めているうちに、私は色々考えてしまった。
あぁ、下を眺めると遠くまで景色が本当にきれいだ。そういえば、眺めると言えば…これまで、私は急な階段の下から上を眺めたらスカートの内側の下着なんかを覗けるかどうかをジックリ考えてみたりしてきたなぁ。それに、SONYの誇る可愛いらしいAIBOの気持ちになって、やっぱり同じく低いAIBOの視点から上を見上げたらやっぱりスカートの内側が覗けるかどうかを考えてみたりしたなぁ。見上げてばっかりだなぁ、しかも、どれもスカートの内側かぁ…。
そういえば、透け透け水着もマズかったなぁ…。あれ、本当に仕事の話から始まったんだけどなぁ…。誰も信じてくれないし…。あぁ、だけど、やはりそんなことを考えていてはいけなかったんだ…。そんなことをしてたから、画像処理追求サイトを目指したハズだったのに、何時の間にか有害サイト認定されてしまったりしたに違いないんだ…。ついには、「こどもに見せられないページ」保証までされたりするしなぁ…
私は一体何処で間違えてしまったのだろう…? あぁ、それにしても地平線がきれいだ…。地平線が丸い…。 あぁ、地球はやっぱり丸いんだなぁ…。
と、まるで「生きる」で「ブランコに乗りながら人生を振り返る」志村喬のように、我が身を振り返っている内に、ふと「そういえば、地平線って一体どのくらい向こうにあるんだっけ?」と考えはじめてしまった。そもそも、地球が丸いからどうしてもある距離以上は見通すことができなくて、それが地平線なわけだけど、それは一体どのくらい先なのだったのだろうか?
おぼろげな記憶を辿ると、意外に地平線は自分の近くにあって、確かほんの数km先程度だった気がするのだけれど…。さて?あれ? はて… 果て…?
というわけで、地平線までの距離を計算してみた。まずは、そのために下図のように視点の高さYと地球の半径Rをとってやる。
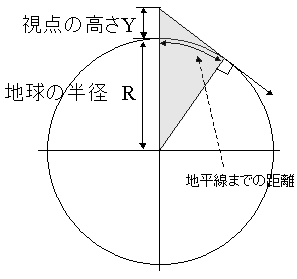 |
「視点位置」と「地球中心」と「地平線」を結んだ三角形(グレーで塗りつぶした部分)がもう簡単なくらいに直角三角形なことに注目して解いてみると、「地平線までの距離」は「視点の高さY」の関数として
というような形になる(計算が合ってれば…)。これに、地球の半径R = 6400kmを代入してやれば、視点の高さYに応じた地平線までの距離が求められるわけだ。
そこで、まずは視点の高さが0〜3m位までの場合をグラフにしてみたのが次の図である。歩き始めて広い世界で暴れだすだろう頃の一才児の身長を緑○、そして、かつてはデカイの代名詞といえばコイツという存在だったアンドレ・ザ・ジャイアントの身長223cmを青○で記入してみた。
青:アンドレ・ザ・ジャイアントの身長 = 223cm  |
このグラフを見ると、一才児の地平線はおよそ3km先にあって、アンドレ・ザ・ジャイアントの地平線は5〜6km先にあることがわかる。もちろん、その間の身長の人達の地平線はその中間、そう4km先くらいにあるわけだ。私たちの地平線はほんの4km先、なんと走ればほんの20分位のところ、歩いても一時間かからない程度の近くに地平線はあるのだった。地平線なんていうと、遥か遠くにあるように思えるけれど、手の届くほんのすぐ先にいるのである。
そして、歩き始めた子供の地平線と巨人アンドレ・ザ・ジャイアントの地平線がたいして変わらない、というところも面白いものだ。あれだけ背が高ければ、さぞかし広い世界を眺めているのだろう、と思ったりするがそういうわけでもないのである。
じゃあ、もう少し高い場所に行くとどうか、ということで1000mまで視点の高さを上げてみたのが次のグラフである。東京タワーの特別展望台の250mを緑○で、あくまで計画中の秋葉原タワーの特別展望台の500mを青○で示してある。 ここまで上がると、250m地点で地平線は60km先になり、500m地点では80km程度先まで見通せることになる。東京駅の位置からの距離で言うと、60kmでは箱根くらい、80kmで三島くらいだろう。
青:計画中の秋葉原タワーの特別展望台 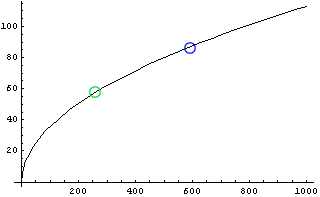 |
調子に乗って、さらに視点を高くしてみよう。先の表富士の五合目2400m地点では200km近く見渡せ、東京駅からの距離で言うと地平線は遠く浜名湖辺りまで離れていく。そして、さらにさらに視点を上昇させ、ジャンボジェット機の巡航高度地上10kmからであれば、なんと350kmほども見渡せるのである。350kmだと東京駅から京都くらいだろうか。東京-京都と言えば、そうちょうど東海道五十三次だ。江戸時代の人達が一月近くもかけて歩いたくらいの彼方まで地平線は後ろへ下がっていくわけだ。地平線は時が流れるにしたがって、遠くに広がっていくのだ。
青:ジャンボジェット機の巡航高度 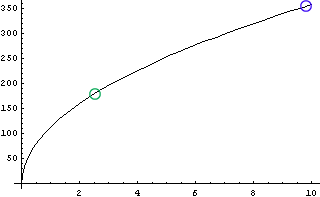 |
そのジャンボジェット機から見える地平線は、かつては一月近くもかけて歩いたくらいの遠く、400kmも遠くなのだから、そこまで行くと地平線が「遥か遠く」に思える。一瞬そう思える、のだけれど実はそんなことはない。ジャンボジェット機の速度からすれば、そんな遥か彼方の地平線だって、やっぱり30分ちょい位のすぐ近くだ。私たちが普通に立っているときの地平線が4〜5kmくらいのすぐ近くにあって、歩いてみればやっぱり30分ちょいで行ける、というのとほとんど同じなのだ。

ジャンボジェット機から眺めた地平線(水平線)
五歳くらいの子供の地平線と、空を飛び回るジャンボジェット機の地平線を時間を距離の単位として比較してみれば実はほとんど同じ遠さだ、というのは何だかとても面白い。大地の果てと天とが接っする地平線はとっても近くにあって、そこまで行くのにかかる時間は小さな子供でも巨大なジャンボジェット機でも同じなのである。
「地平線」なんて言うと、まるで「手が届かないもの」の代名詞みたいに使われたり、あるいは「その先には何があるのかわからないもの」の代名詞に使われたりするけれど、ちょっと行こうとして見れば、片道30分ちょっとでその「地平線」まで辿りつくことができるわけだ。案外、遠くにあると思い込んでいるものも、手を伸ばしてみれば、もしかしたら手が届くものなのかもしれない。しかも、それは地平線まで辿り着く時間が小さな子供でも巨大なジャンボジェット機でも同じだったように、誰でもできたりするものなのかもしれない。
もちろん、かつての「地平線」だった場所まで辿り着いたとしても、新しい「地平線」は視界の向こうに下がって行くわけなのだけれど、そこまでだってやっぱり歩けばほんの30分だ。遠い空の果て、地平線の向こうは、すぐそこだ。
2001-07-31[n年前へ]
■水平線の彼方 
Over The Horizon
先日、富士の五合目から地平線を眺めていたのだけれど、そこで「水平線の向こうには何があるのだろう?」なんてことをふと頭に浮かべてしまった。「そこまでしか見通せない」という線が水平線なのだから、もちろん水平線の向こうに何があるのか見えるわけがない。だけど、だからこそ「その水平線の向こう」に何があるのかが、少しばかり気になってしまった。

そういえば、少し前に英和辞書を読んでいた時に、" on [over] the horizon"で「兆しが見えて,将来起こりそうで」を意味する、なんて書いてあった。「水平線の向こう、水平線の彼方」にある「何か」は「将来起こりそうな、何かの兆し」というわけだ。
あぁ、そうかぁ、と私は思わず納得してしまった。確かに、水平線の向こうに例えばもし何かの波があれば、それはきっといつか私たちの目に見えるようになって、そして私たちの足元にまで辿り付くことだろう。水平線の向こうにある波は止まることなく進み続けているのだから、例え水平線の向こうにあっても将来必ず私たちの場所まで辿り着くのである。
もちろん、水平線の向こうにある波を私たちが見通すことはできるわけはないのだけれど、だけどその気配を私たちはきっと感じるのだろうと私は思う。「水平線の彼方」にあるものは、「将来起こりそうな何かの兆し」であって、水平線の向こうにいるその気配には強い存在感があるはずだろう。
そんな「水平線の彼方にある波」を考えるとき、私はこんな話を思い出す。
地球はよく「水の惑星」と呼ばれる。確かに、そう呼ばれるくらいに地球には水が溢れている。何しろ、地球の表面積の七割が海なのだ。しかし、そうは言っても、地球の表面が全部水に覆われている、というわけではない。私たちが生活している陸地だって、「残りの三割だけ」とはいえちゃんと存在している。それなら、表面全部が水で覆われている「水の惑星」がもしもあったとしよう。そんな水の惑星のどこかで高い津波が生じたら、一体どうなるだろう?例えば、その水の惑星の南極である日突然津波が生じたとしよう。その時その津波はどんな風に伝わっていくだろう?
その津波の動いていく様子を図示してみたのが、下のアニメーションだ。
自分と正反対の場所で生じた波が自分の足元まで辿り付いて、生まれた場所と正反対の場所で生まれた時と同じ大きな津波になっているということを考えると、どうしても不思議な感覚に襲われる。そして、自分と正反対の場所で自分の足元で生じているのと同じ高波が生じている、ということもまたちょっと不思議だ。まるで、自分と正反対の場所に「もう一人の自分」がいるみたい、だ。「もう一人の自分」が、自分からは見えない水平線の向こうにいるなんてちょっと面白い感覚だ。
南極(図の下部)で発生した津波は進むに従って、段々と小さくなっていく。最初は南極の一点に集中していたエネルギーが段々と広がって拡散していくのだから、波が進んでいくにつれその高さはどんどん低くなる。そして、赤道を通過する頃には津波の高さはとても小さくなってしまう。ところが、その波が赤道を過ぎたとたんに津波は逆に強まりはじめる。赤道を通過した後は、津波の前方はだんだんと狭まっているので、こんどは津波のエネルギーが集まり始めるわけだ。それまでは、低くなる一方だった津波の高さは、今度は逆に徐々に高くなっていく。そして、ついに津波が北極に辿り着く時には、かつて南極で津波が発生したときの高さを再現してしまう。生まれた地点のちょうど反対側で、津波が生まれたときと全く同じ高波が発生するのである。
私たちの裏側で津波が発生したとしても、その津波は徐々に小さくなりながら進み続け、そして私たちの足元でその津波は再び大きな高波となるのである。そして、その津波はその後も同じように進み続けて、また南極で大きな高波となる。南極から発した高波がもう一度南極に集まってまた高波となるとも言うことができるかもしれないし、あるいはそれは、北極で集まった高波が南極で集まってもう一度同じ高波となる、とも言えるだろう。
そしてまた、「水平線の彼方にある波」はそれと似たこんな話も思い出させる。
宇宙の曲率が正で閉じた球状空間だった場合、私たちが発した光はどうなるだろう? 私たちからどんどん離れて行く光は空間の四方に広がって行くが、何時の間にかその光は徐々に近づき始める。そして、はるか彼方のある一点でその光が集まり、そしてまたその光は広がり始める…。そしてついには、その光は私たちのいる場所に集まり始める。私たちを取り囲む全ての方向から、かつて自分が発した光がやってくることになる。かつての自分があらゆる方向に見え出すのである。
水平線の彼方には何があるのだろう?水平線の向こうを見通すことは、私たちにはできないけれど、遥か彼方にいる波は「将来必ず私たちの足元に訪れる」。そして、もしかしたらそれは「かつての自分が発した波」かもしれないし、「どこか自分と正反対の場所にいる誰かが発した波」かもしれないし、それは廻り回ってやっぱり、「自分が発した波」なのかもしないし、やっぱりそれとも…なんて考えてしまったのである。
2001-11-22[n年前へ]
■あなたと見たい、流星群 
同じ流星が見える距離
「しし座流星群」が美しく盛んに空を彩った翌朝、Fast&FirstのBBSをぼんやりと眺めていると、「アナタとみたい流星群」と題した
「僕たち距離は離れているけれど、同じ星(月)を見ているんだね」という書き込みを見かけた。思わず良い話だなぁ、と見入ってしまった。
なんて会話をする二人がいます。だけど、一体離れている距離が何km位までなら同じ流星を見ることができるのでしょうか?
今年の「しし座流星群」のようなきれいな流星群を、深夜同じ場所に佇んで二人で一緒に同じ流星を眺める人達も多いだろうが、離れた場所から、それでも同じ流星を眺めている二人もいることだろう。「そんな遠く離れた二人が、同じ流星を眺めることができるとしたら、それはどの程度の距離までなのだろう?」という「同じ流れ星を眺めることができる二人の距離」だなんて、とてもロマンティックでとても面白い話だなぁ、とその書き込みを眺めながら思った。そして、これはいつか考えた「地平線問題」と同じだなぁと考えて、だけど何故だか少し切ない話だなぁ、とも感じた。
だから、とても興味を惹かれたのだけれど、その切なさのせいか、ただぼんやりとその話を眺めていた。すると、すぐに「今日の必ずトクする一言」のKOROKAN氏が
これは計算が可能ですね。…流星の輻射点から地球に接線を引きます。そうすると、と簡潔な答えを書きこまれていた。暗算で片付けるところはやはりさすがスゴイなぁ、なんて感心していると、それとほとんど同じ頃、hirax.netの「ぐるぐる検索」にも、元の質問を書き込まれていた方から、
地球の中心、輻射点、接線が地球に接する点の直角三角形になりますね。…(中略)…これに地球の半径をかけると1118kmと出ました。
つまり半径1118kmの範囲が輻射点から見えることになりますから、(二人の距離としてはその二倍の2000kmで)おそらく東京−福岡、東京−札幌の遠距離恋愛なら見えるかも。
あなたと私、離れていても同じ星を見ている。何kmの距離まで離れていても同じ流星を二人は見ることができるのでしょうか? (F&Fの掲示板に書きこんだ内容に同じです。)という検索メッセージが送られてきた。そして、さらに
とても好きな女性が私の住むミネソタから約1000マイルほど離れたオハイオに住んでいまして、彼女に獅子座流星群の話をしながらこの話を思いついたのです。ちょうど1000マイルだったらギリギリって感じかもしれない?遠く離れた場所でも、同じ流星を見ることができるかもしれない?という話の発端を読みながら、私もちょっと落書きをしてみた。
KOROKAN氏が簡潔に書かれていた答えをもう少し言い換えると、「私たちが流星を見ることのできる距離」は「流星の地平線」と同じだ。私たちが流星を見ることができるのであれば、逆に流星からも私たちが見通せることになるのだから、「地表に立つ私たちが流星を見通せる距離」=「流星が地表に立つ私たちを見通せる限界」、ということであって、それはすなわち「流星の地平線」そのものということになる。もちろん、本当はもっと色々なことを考えなければならないわけだけれど、とりあえずはこんな大雑把な計算でも十分だろう。
●流星の発光点  |
以前、地平線までの距離を計算した
でやったものと同じく(KOROKAN氏が書かれていたことと同じ)、灰色の直角三角形に着目してやると、流星の発光点の高度がわかれば、あとは地球の半径=約6400kmを用いれば、流星の地平線までの距離は簡単に計算することができる。 流星の発光点の高度は理科年表をめくると、次のような表が載っていて、大体70km〜130kmの間であることが判る。その高度差を100kmほどの長さにわたって、光りながら駆け抜けて行くのである。
 |
そして、「流星の発光点の高さY」を変えた場合の、流星から見渡せる距離(=流星の地平線)を計算してみたものが次のグラフになる。この「流星から見渡せる距離」がつまりは「流星を見ることができる最も長い距離」になる。
 |
先の「流星の発光点の平均高度」として約70km〜130kmという値を使うと、先にKOROKAN氏が書き込まれていたように1000km前後という数字になるわけである。で、流星の発光点(輻射点近く)を挟んで遠く離れたところに住む二人であれば、その二人の距離が1000kmの二倍で2000kmの距離までは同じ流星が見える、ということになる。
だけど、これは理想的な話で、現実の話ではない。
実際にはそんなわけにはいかない。私達が住むほとんどの場所は、海原の真中や高い山の頂きじゃない。私達が流星を眺める場所はビルや鉄塔に囲まれたマンションのベランダだったり、あるいは木々や小高い山が周りを囲む小さな公園だったりする。少なくとも、地平線の果てまで見通せるような場所で眺める人なんかほとんどいないだろう。流星を眺めようとするほとんどの人達がいる場所は、上に広がる空しか見えなくて、地平線近くの空なんか見えない場所だとう思う。きっと、せいぜい天頂から60〜70°位の角度までしか空を見通せないに違いない。
だとすると、さっき計算のときに着目した「灰色の直角三角形」は少し変えてやらなければならない。人の視点での地球への接線をひくのではなくて、もう少し天頂側へ角度を振ってやる。すると、先の「灰色の直角三角形」は下の図のように「青色の三角形」に変化することになる。
●流星の発光点  |
そして、先と同じようにこの三角形に注目しながら、「限られた空の下」に住む現実の私達が見ることのできる流星までの距離を計算してみると、下のグラフのようになる。下のグラフで「空を見渡せる角度」が天頂からの角度で90°、すなわち地平線まで完全に見渡せる場合である。つまり、先に計算した「理想的な場合」である。そして、それが1100km程度というのはもちろん先程と同じだ。
 |
このグラフを眺めてみると、天頂からの角度に対しての「見ることができる流星までの距離」は「地平線近く」の場合とそうでない場合とで全然違うことが判るだろう。
「地表面」と「その100km上空の面」というのはほとんど平行だから、天頂からの角度が70°位までは「流星の発光点までの距離」は緩やかに増加していくだけだ。天頂からの角度が70°(というとかなり水平にもう近いが)の時でさえ、「流星の発光点までの距離」はたった200km強である。さきほど見えると思われた1000kmなんて遥か彼方だ。
しかし、天頂からの角度が80°を超え、ほとんど水平間際になってくると、「見ることができる流星までの距離」はぐんぐんと大きくなってゆく。80°で600kmくらい、85°で700kmくらい、そして90°でついに1000kmの彼方の流星まで見えることになる。
ということは、現実の私達、海原の真中や高い山の頂きじゃなくて、ビルや鉄塔に囲まれたマンションのベランダや小さな公園から流星を眺める「限られた空」の下に住む私達は、せいぜい200kmくらいまで離れた場所で光る流星しか見えないことになってしまう。1000kmの彼方の流星なんかとてもじゃないが見えなくて、たった200kmが限界になってしまうのである。
すると、遠く離れた二人が同じ流星を眺めようとするとき、その二人の距離の限界は高々200kmx 2=400km程度ということになってしまう。東京-大阪でも難しいかもしれない。空が本当に天頂近くに限られて、「空が無い」東京のような場所であれば、きっとその距離はもっとずっとずっと短くなるはずだ。新幹線に乗って会いに行くような二人では、同じ流星を眺めることはできないのかもしれない。
だけど、とも思う。先のKOROKAN氏の書き込みは
それに何より、「見ているモノが同じモノ」と信じる力が重要で、それが同じモノか、別のモノかを証明するすべも、否定するすべもありませんなあ。信じる者は救われるというし。という風に締めくくられていた。私も本当にその通りだと思う。さっきの「せいぜい400kmが限界」なんて計算結果は「同じ流星を眺めようとする二人」には全然関係ないのだろう、とも思う。
もしも、遠く離れて見渡せる空が全然重ならないような距離であっても、例えそれが昼と夜ほどの違いになる距離であっても、同じ景色を眺めている二人もいるだろう。また、逆にとても近くにいても同じ景色も流星も眺めることのできない二人もいるのだろうと思う。そんな違いを決めるのは、幾何学的な話じゃなくて、きっと別の何かだ。
そしてまた、流星を眺める私たちの視点から、流星の視点に移動するといろいろなものが見えてくるとも私は思う。「限られた空」の下の私たちの視点がもう少し高く、高度100kmほどまで上がれば、周りではついに流星が輝やき燃える高さになる。ここまでくれば、見渡すことのできる地平線の果てまでは1000kmほどになる。その半径1000kmの円の地表が、その流星の視点から見える世界だ。
そして、その流星の地平線の中にいる人達は、その流星を同時に眺めることができる人達であるが、一体その半径1000km程の領域の中にはどれだけの人達が住んでいることだろう?数千人?それとも、数千万?とてもたくさんの人達がいるに違いない。それは例え、半径200kmの円であってもやはり同じことだろう。その地平線の中にはとてもたくさんの人が住んでいる。
そんな地平線の中の(あるいは外の)数え切れない沢山の人達の中に、同じ流星を眺めようとする二人がいる(それともいない)なんて、やっぱりとてもロマンティックで、やっぱりちょっと切ない話だなぁ、と思う。