1998-11-12[n年前へ]
■無限音階を作ろう 
上昇し続けるって何ですか?
無限音階を作りたい
無限音階というものがある。ド・レ・ミ・・・と音がどんどん高くなっていくように聞こえるのだが、いつまでたっても終わらず、ふと気づくとずっと前と同じような音の高さだというものである。Escherの無限階段の版画は有名だが、あれの音階版である。とにかく、無限音階を作ってみようというのが今回の目的である。参考までに、Eshcerのことに関しては藤原康司氏のWEBhttp://www.pluto.dti.ne.jp/~fwhd5468/に詳しい情報がある。 ちなみに、このような版画である。
 |  | 「上昇と下降」(左図、1960年作) 「滝」(右図、1961年作) |
無限音階の仕組み
人間の聴力にはもちろん周波数特性がある。ニコンの補聴器のWEBhttp://www.nikon.co.jp/main/jpn/society/hocyouki.htm
によれば20Hz-20kHzが通常聞こえる周波数の範囲であるという。例えば、CDのサンプリング周波数はが約40kHzであるのは、この20kHzの倍だからである。つまり、ナイキスト周波数による。
もし、ある高さの「ド」の1オクターブ下、そのまた下、...それだけでなく、1オクターブ上、そのまた上...が一度になったら、人間の耳にはどう聞こえるだろうか。それは、やはり「ド」である。その時のスペクトルはこんな感じである。なお、横軸は2をベースにした変形の対数軸である。また、実際には「ド」ではない。
 |
それでは、そのような「レ」が鳴ったとしたら?もちろん、それも「レ」である。そのようにして、「ドレミファソラシド」とやるとどうだろう?最初の「ド」と最後の「ド」は全く同じになっている。しかし、人間の感覚としてはどんどん音の高さが上昇していくように感じる。これが無限音階の仕組みである。
図で示すとこのようになる。なお、下の図中で水色は人間の耳に聞こえる周波数領域である。また、振幅はたんなる相対値である。
 |
 |
 |
 |
 |
作成した無限音階
今回は12音の平均率音階を用いている。音階そのものについては「音階について考える」という別の話である。また、基本波形としては正弦波を用いている。20Hz以下の正弦波を基本波形として、その倍音を20kHz超まで均等に足しあわせたものをただ作っただけである。正弦波を用いたのは話を単純化するためである。ここに今回作成したMathematicaのNoteBookを置いておく。また、下が作成する途中のデータである。どこか間違っているような気もする。少し不安だ。
 |  |
 |  |
さて、これが作成した無限音階である。それっぽく聞こえるだろうか。
1998-12-30[n年前へ]
■12月のサナトリウム 
とある診療所に行った。
 |
今は使われていない部屋の風景。
 |
昔の機械が雑然と置かれている。
 |
診療所で療養していた人達の名簿もある。名を聞いたことのある多くの人がいた。
この診療所はある高原の中腹に建っている。
 | 先の療養所内の一室の写真は、この写真の2階の中央の部屋にあたる。 |
 | このような療養所へ入ることのできなかったもっと多くの人も、やはり同じような窓を眺めていたはずだ。 かつては、結核にかかった人が寝ている部屋、めったに開かない窓、というのはよくある風景だったという。そして、その人達が出てくることはなかった。 |
1999-11-23[n年前へ]
■ミニスカートの幾何学 
32cmの攻防戦
早朝、東名高速で事故渋滞にはまってしまった。仕方がないので、TVを眺めていると、面白い話をやっていた。それは、ミニスカートの丈の話である。何でも、最近の流行はミニスカートの丈が32cmのものであるらしい。女子高生?などが言うには、
「34cmだと長いしぃ。」だから、32cmだと言うのだ。別に、オリンピック選手でもないのだから、ミニスカートの丈の限界まで挑戦しなくても良いだろう、と私などは思ってしまう。しかし、彼女たちはそう考えないらしい。人それぞれである。
「30cmだと下着が見えちゃうしぃ。」
それにしても、スカートの丈が32cmと30cmの間でそんなに、違いがあるものだろうか? 「見える・見えない」を決める分水嶺がその2cmの違いにあるものなのだろうか? 妙に不思議である。 そこで、ミニスカートの幾何学について考えてみることにした。題して「32cmの攻防戦」である。
何より先に確認しておくが、私は今回は科学的好奇心で動いているのである。そこに、一点の不純な気持ちも存在しないことを、ここで確認しておく。いや、むしろ、女性のためのミニスカート理論の構築を目指しているといっても良いかもしれない。といっても、信用されないとは思うのであるが...
 |
さて、先のTV番組によれば、腰からスカートの先までの長さを「スカートの丈」というらしい。また、先のTV番組により、「腰から下着の一番下の部分(股下を計るときの一番上)までの長さが大体25cmである」という重要な情報を得ることができた。
それでは、解析を始めてみよう。以下に、今回考えた「ミニスカートの幾何学」を示す。なお、今回使用する長さの単位は全て(cm )である。
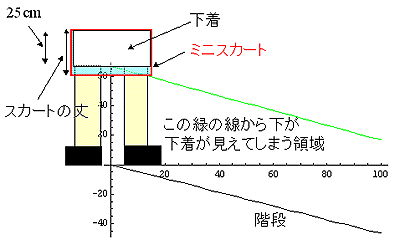 |
まず、階段の途中に立つミニスカートを履いた女性の下着中央部分とミニスカートの最下部を結ぶ直線を考える。この線よりも下が、下着が見えてしまう領域である。もちろん、階段の下には潜り込めないわけであるから、その線と階段で囲まれた領域内から見た際に下着が見えてしまうわけだ。その線のことを「下着防御ライン」と呼ぶことにする。
さて、ミニスカートの形状を考えよう、スカートの丈はもちろん入力条件としてわかる。すると、足りないパラメータは幅である。そこで、ヒップ周りが88cmとしてスカート中央から端までの長さ(rcm)を求める。2πrが88cmであるから、
r = 14cmとなる。
また、駅などの階段というと25度位だろうか。30度というとかなり急な階段である。湘南通商の階段とか急な階段は色々あるが、今回は急な階段の斜度として、25-30度位としておく。ちなみに、京都駅北口のエスカレータで実測したところ、25,6度であった。
それでは、スカートの丈が32cmで階段の角度が30度である場合の計算をしてみる。女性の股下は仮に70cmであるとしておく。おそらく、身長160cm位であれば、この程度であろう。
それでは、ミニスカートの丈が32cm、30cmの時の「下着防御ライン」を計算したものを示す。
 |  |
緑、すなわち、ミニスカートの丈が32cmの時は「下着防御ライン」は階段とほぼ平行である。それに対して、丈が30cmの時の「下着防御ライン」は、ミニスカートを履いた女性から離れるほど階段よりも上に離れていく。ということは、人間の視点位置が「下着防御ライン」を越えるということである。すなわち、下着が見られてしまうということだ。
階段と「下着防御ライン」の差、すなわち、人の目の高さがこの程度ならミニスカートの下の下着を見ることができる、というものを示してみる。
 |
32cmの丈の場合、10m(1000cm)離れても、目の高さが150以下の人しか「下着防御ライン」を突破できない。すなわち、女性は事実上「下着を見られる恐れがない」といって良いだろう。もちろん、20mとか離れたら別である。しかし、超人的な視力がなければ、そのような条件下で下着を確認することはできないであろう。
それに対して、30cmの丈の場合には6m離れた時点ですでに視点が2mの位置にある人でも「下着防御ライン」を突破できてしまう。これでは、「全ての人に下着を見られてしまう」ということになる。
もし、女性の身長が20cm程度高く、180cm程度であったら、どうなるだろうか。おそらく、股下長さは10cm程度長くなる。すると、上の図(階段と「下着防御ライン」の差)の緑、赤ラインは10cm程度高くなる。それでも、緑の32cmスカートの「下着防御ライン」はやはり安全圏といえるだろう。
また同様に、厚底サンダル・ブーツなどを履いた場合には股下長さが20cm弱高くなると考えられる。この影響を考えると、長さとしては身長の影響よりも大きいわけである。それは、身長の1/2が股下長さの増加に繋がるのに対し、厚底靴の長さはそのものずばり股下長さの増加に繋がるからである。しかし、それでもやはり緑の32cmの「下着防御ライン」は安全圏である。
すなわち、32cmと30cmのスカートの丈の長さの間には、「下着が見える・見えない」に関する分水嶺が確かに存在するのだ。先の、
「30cmだと下着が見えちゃうしぃ。」という発言は理論的に裏付けられたのである。
それでは、次に階段の角度が25度である場合の計算をしてみる。
 |
緑の線、すなわちスカートの丈が32cmの場合の「下着防御ライン」が階段にどんどんすり寄っているのがわかると思う。すなわち、「下着防御ライン」はより強固なモノとなっているのである。階段と「下着防御ライン」が女性から離れるほど近づくのである。次に、階段と「下着防御ライン」の差を見てみよう。
 |
緑線、すなわちスカートの丈が32cmの場合に注目する。 女性から、離れても、近づいても、何人たりとも、下着を見ることはできないのだ。下着がシュバルツシルト半径の中に隠されるといっても良い。女性の安全を確保する「完全安全条件」を満たす「下着防御ライン」が完成されているのだ。
これは階段と「下着防御ライン」が平行である条件を境として、そのような条件が達成される。その条件よりより「下着防御ライン」が強固になると、誰も「下着防御ライン」を突破することはできない。すなわち、「完全安全条件」が達成されるのである。
この絶対に下着を防御可能(「完全安全条件」)な「完全安全条件」とは、階段と「下着防御ライン」が平行である条件であるから、ミニスカートの丈(xcm)をパラメータとして、
Tan[階段の角度] = (x-25)/14で計算することができる。ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である。もちろん、極端な安産体型の場合には、その14という値を適当に補正する必要がある。
さて、この条件には女性の身長(股下長さ)は関係しないところが面白い。もちろん、厚底サンダルなどを履いても同じである。もちろん、若干の影響はあるが、あまり影響はない。
さて、今回の「ミニスカートの幾何学」の考察により、判明した結果をまとめてみよう。
ミニスカート内部の下着が「見える・見えない」には
- ミニスカートの丈が30cmと32cmの間に、分水嶺が確かに存在する
- 絶対に下着を防御可能(「完全安全条件」)なミニスカートの丈(x cm)とは、Tan[階段の角度]= (x-25)/14 により決定される
- ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である
- 極端な安産体型の場合には、その14という値を適当に補正する必要がある
- 一方、ミニスカートを履いている人の身長はほとんど影響を及ぼさない
- 厚底サンダルの方が身長よりは影響を及ぼすが、それでもほとんど影響はない
ミニスカートを身につける女性の経験に基づく、「30cmだと下着が見えちゃうしぃ。」理論はなかなか正しいことがわかる。経験というものを軽んじてはいけない、という良い?例かもしれない。結果の伴わない理論に価値はない、ということだろうか。
それにしても、厚底ブーツにミニスカートを履いた女性達は、ロールプレイングゲームの主人公達のようだ。色々なアイテムを手に入れ、冒険を続けている主人公達のようである。ほんの少しだけ、うらやましいような気もする。
さて、こういう話題を書くと少し不安がある。もちろん、私もミニスカートを見ると、妙に心が落ち着かないのも確かに事実ではある。しかし、だからといってことさらに興味津々というわけでもない、と思う。多分。ということで、「できるかな?」の女性読者の数が減少しないことを、ただ祈るのみである。
2000-06-13[n年前へ]
2000-11-19[n年前へ]
■螺旋階段のアリス 加納朋子 
今日、買った本。「だってそうでしょう?箱は開けてみなきゃ、中身はわからない。電話は出てみなきゃ、相手はわからない… 少なくとも、旧式の電話はね。人の心だってそうよ。こうして…」「-ノックしてみないと、わからないの」