2009-01-09[n年前へ]
■経済に関する時系列データを眺めてみる 
Mathematica は数式処理向けアプリケーションというよりも、数式処理も得意な「プログラミング言語」です。最近のバージョンでは各種データ取得関数が豊富ですから、さまざまなデータを眺めた後に解析する、といったことが簡単にできます。
不景気なニュースばかりが続きます。そんな今が、一体どんな時代なのかを眺めてみたくて、今日は経済統計データをMathematicaで（まずは）眺めてみることにしました。
右のグラフは、1930年頃から現在までのダウ平均株価(工業株30種平均株価)です。工業株と名付けられてはいますが、30種の採用銘柄を見ればわかるように、平均株価を算出する30の会社は、社会の動きを反映するような広い業種から選ばれています。
80年近くにわたる「ダウ平均株価の変化」を眺めていると、「データ解析」「要因解析」などをしたい、と感じる人が多いのではないでしょうか。何だか20年ほどの上昇と20年ほどの下降（停滞）を繰り返しているように見えてきたり、短周期の上下動があるように思えてきたりします。そこで、そういったものが本当にあるのか・理由は何なのか、ということを知りたくなる、つまり、長期的なトレンド（傾向）、周期的な変化、それらをもたらす要因・・・そんなことを調べ・知りたくなる人も決して少なくないだろう、と思うのです。
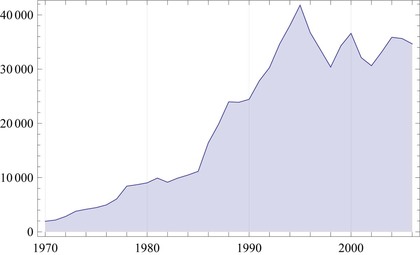さて、次に眺める右のグラフは、（人口で正規化した）日本の国内総生産(GDP)です。1970年から現在までのデータですが、大雑把にはダウ平均株価と同じ動きになっています。また、1990年半ばから現在までは、上下動はあるものの、停滞し続けているように見えてきます。
こうした統計データをグラフにし眺めていると、世界全体や各国の「景気」の変化というものについて、もっと詳しく知りたくなります。たとえば、景気の動きが持つ周期性、景気循環というものについて知りたくなったり、そういったものを生み出すに至った世界史というものを、もっと知りたくなります。各時代に、世界各国で、どんな生活や文化が生まれ、どんな産業が生まれ・どんな業種が衰退していったのか、ということを学びたくなるのです。
以前、経済学者に経済学を教えてもらいにいった時にも、経済学が生まれる少し前から現在までの歴史を知りたくなり、世界・歴史年表を自分なりに作ってみたりしました。それは、どんな経済事象も、あるいは、経済学者たちの研究もすべて（その）時代背景に応じていた、と教えられたからです。
物理学者の寺田寅彦は、「科学と文学」の中でこう書きました。
歴史は繰り返す。方則は不変である。それゆえに過去の記録はまた将来の予言となる。20世紀の歴史、あるいは遙か昔からの歴史を学び直し、過去の記録を通して未来の世界を覗き眺めてみたくなります。未来に向かって世界がどのように動いてゆくのか、それを知るために、過去を紐解き知りたくなります。
寺田寅彦 寺田寅彦随筆集 (第4巻)
今日は、図書館に行ってみることにしましょうか。過去の歴史や物語が収められている図書館は、未来への予言が詰まってる場所なのでしょうから。
2009-01-21[n年前へ]
■コロンビアは麻薬用作物からの所得をGDPに算入している
「スティグリッツ入門経済学 <第3版>」を読んで、意外かつ納得したのが、こんな一節だ。
不法な経済活動はGDPに算出されない。（中略）しかし不法な経済活動が主要な所得源泉となっている国についてはそうではないだろう。この場合には、そうした所得をGDPの一部として計算しないとなると、その経済を誤って理解することになるかもしれない。「アメリカの高校生が学ぶ経済学 原理から実践へ」がとてもわかりやすかったのと同じように、この本も実に「全体を通した流れ」を納得しやすい。ぜひ、いつでも持ち歩くことができるような文庫本で出して欲しい。
（中略）
コロンビア政府は、不法な麻薬作物から得られた所得をGDPに算入するように計算方法を変えた。GDPの計算において麻薬用作物を合法的な作物と同じように取り扱うと、コロンビアのGDPは1%程度増加することになる。
2009-10-04[n年前へ]
■IronRubyとMathematica Playerで経済データも自由自在
本当に、「(.NETで動くRubyである)IronRubyと(無料配布されている)Mathematica Player」を組み合わせたツールの可能性は無限大だ、と思います。しかも、その組み合わせが無料だというところがまた素晴らしいです。素晴らしすぎて、「そういう実装でウルフラム・リサーチは良いと考えているのだろうか？」と疑問に思ってしまうくらいです。
今日の例題は、MathematicaのCountryData関数を使って、日本の最近40年間くらのGDP(国内総生産)を習得してみることにします。書くコードはこんな感じです。
include System
require 'Wolfram.NETLink'
include Wolfram::NETLink
kernelLink=
MathLinkFactory.CreateKernelLink()
kernelLink.WaitAndDiscardAnswer()
gdp=kernelLink.EvaluateToInputForm(
'CountryData["Japan", {{"GDP"}, {1970, 2008}}]', 0)
puts gdp
kernelLink.close
これで、1970年から2008年までの日本の国内総生産(GDPデータ)が時系列的に手に入ります。ちなみに、結果はこういう形式で返ってきます。
{{{1970, 1, 1, 0, 0, 0}, 2.0295777757538376*^11}, {{1971, 1, 1, 0, 0, 0}, 2.2925 011052164844*^11}, {{1972, 1, 1, 0, 0, 0}, 3.0359415844215283*^11}, {{1973, 1, 1 , 0, 0, 0}, 4.124671054658262*^11}, {{1974, 1, 1, 0, 0, 0}, 4.578535174149201*^1 1}, {{1975, 1, 1, 0, 0, 0}, 4.978680032023408*^11}, {{1976, 1, 1, 0, 0, 0}, 5.59 553536053367*^11}, {{1977, 1, 1, 0, 0, 0}, 6.886633644946532*^11}, {{1978, 1, 1, 0, 0, 0}, 9.675983051549285*^11}, {{1979, 1, 1, 0, 0, 0}, 1.0071187368835983*^1 2}, {{1980, 1, 1, 0, 0, 0}, 1.0552047308073224*^12}, {{1981, 1, 1, 0, 0, 0}, 1.1 662277105414326*^12}, {{1982, 1, 1, 0, 0, 0}, 1.0838309489751625*^12}, {{1983, 1 , 1, 0, 0, 0}, 1.182236662061611*^12}, {{1984, 1, 1, 0, 0, 0}, 1.258002926042118 4*^12}, {{1985, 1, 1, 0, 0, 0}, 1.3467326711952527*^12}, {{1986, 1, 1, 0, 0, 0}, 1.9954327828900427*^12}, {{1987, 1, 1, 0, 0, 0}, 2.4200293838043384*^12}, {{198 8, 1, 1, 0, 0, 0}, 2.9383777035023525*^12}, {{1989, 1, 1, 0, 0, 0}, 2.9401349260 95067*^12}, {{1990, 1, 1, 0, 0, 0}, 3.018112125973376*^12}, {{1991, 1, 1, 0, 0, 0}, 3.4512768484608447*^12}, {{1992, 1, 1, 0, 0, 0}, 3.766884938703116*^12}, {{1 993, 1, 1, 0, 0, 0}, 4.3237911294441895*^12}, {{1994, 1, 1, 0, 0, 0}, 4.76016480 3785754*^12}, {{1995, 1, 1, 0, 0, 0}, 5.24425055236488*^12}, {{1996, 1, 1, 0, 0, 0}, 4.620457424448448*^12}, {{1997, 1, 1, 0, 0, 0}, 4.2337825304782827*^12}, {{ 1998, 1, 1, 0, 0, 0}, 3.8422661071666924*^12}, {{1999, 1, 1, 0, 0, 0}, 4.3476506 956717817*^12}, {{2000, 1, 1, 0, 0, 0}, 4.649614280538379*^12}, {{2001, 1, 1, 0, 0, 0}, 4.0877256836277627*^12}, {{2002, 1, 1, 0, 0, 0}, 3.904822831192468*^12}, {{2003, 1, 1, 0, 0, 0}, 4.231254569386364*^12}, {{2004, 1, 1, 0, 0, 0}, 4.58488 9737074735*^12}, {{2005, 1, 1, 0, 0, 0}, 4.559019715540946*^12}, {{2006, 1, 1, 0 , 0, 0}, 4.434993203595208*^12}}つまり、時間と国内総生産を並べたリスト形式で返ってきます。
もちろん、日本のGDPだけでなく、任意の国のGDPでも、どこかの企業の株価でも、それがどこのマーケットでもいつの時代でも、（基本的には）関数一つで手に入るようになります。もちろん、入手したデータの処理をすることだって、至極簡単です。経済問題をコメンテーターのように評論している文章を見ると、「データを自分で扱い、自分で咀嚼・消化してから話して欲しいものだ」と思ったりしますが、そういった作業を簡単に自分の手で行うことができます。競馬や競輪、はたまた、競艇予想のごとく、経済や株価の行方を実証・予想してみるのにも、IronRuby+Mathematica Playerの組み合わせなら簡単至極にデータ九取得・処理を行うことができます。
これが、最近のMathematicaの便利さでもあり、無料のMathematica Playerを使うことでそのMathematicaの機能を自由にシームレスに使うことができる「(.NETで動くRubyである)IronRubyと(無料配布されている)Mathematica Player」の組み合わせの凄さでもあります。
「データの見せ方」「ビジュアライズ」はとても大切です。けれど「データそのものを手に入れること」「データを加工・処理すること」の重要性は、決して「ビジュアライズ」に劣るものではありません。基本的には、それらすべてが優れていることが理想的であり、現実的には、それらの中で一番弱い部分が相和の効果・力を決めると思っています。
無料で使うことができる Mathematica Playerの一番の便利さ・凄さは、「データ取得」「データ処理機能・言語機能」に関して、本家本元のMathematicaに比べて決して劣っているわけでなく。基本的にはほぼそのままの機能を使うことができるようにしている、というところにあるように思えます。
Rubyから透過的に、Mathematicanを使って入手・計算可能なデータをそのまま自由自在に使うことができる、というのは意外なほどに凄まじい機能拡張だとは思いませんか…？
2013-01-15[n年前へ]
■「”1人あたり”GDP(国内総生産）の地球儀」で「日本の豊かさ」を考えてみよう!?
生み出したもの…つまり何か新たに加えられたものの価値が「いくらになるか？」…それを表したものが「GDP(国内総生産）」です。生み出したものと交換されたお金の量…つまり生み出されたものに付けられた値段が、回り回って私たちのお財布に入ってくるわけですから、GDP(国内総生産）は「儲かり具合」のモノサシになったりもします。
世界各国のGDP(国内総生産）を眺めると、ここ数年は、１位アメリカ合衆国、２位中国、３位日本…という順位が定番です。以前は２位を占めていた日本を、2009年以降は中国が抜き去っています。ちなみに、４位以降はドイツ・フランス・イギリスといった国々が常連です。
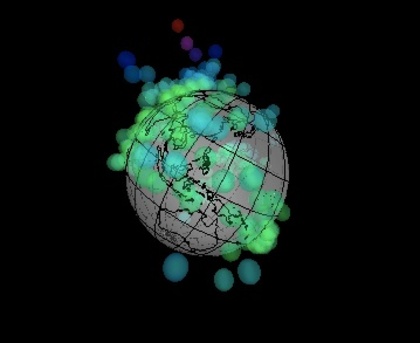そんな中国の躍進を見て「中国は人口が多いからなぁ…1人あたりGDPで見ないと1人あたりの豊かさはわからないよなぁ」と考えたりもします。…けれど、実際に「”1人あたり”GDP(国内総生産）」を眺めてみると、「中国は人口が多いからなぁ…1人あたりGDPで見ないと…」という言葉は、自分たちに跳ね返ってくることに気づきます。
たとえば、下に貼り付けた動画（と右に貼り付けた画像）は、世界240 国の経済データを使って「”1人あたり”GDP(国内総生産）をプロットしてみた地球儀」です。１人あたりの名目GDP(USドル)が高いほど、高い場所に印を付けてみたもので、日本は240国中では17番目です。上位の国は、 ルクセンブルク・カタール・ノルウェー・スイス・オーストラリア…という具合です。「”1人あたり”GDP(国内総生産）の地球儀」を眺めてみると、ヨーロッパ一体が何やらとても華やかに見えてきます。
上位の国々は、「１人あたり金額」にすると日本の２倍以上…日本の豊かさは一体どんなものなのでしょうか。GDPの高さや税金の高さ…色んな「額」を眺めることができる「地球儀」が学校の教室にあると、色んなことを感じることができそうです。
2013-01-16[n年前へ]
■「1人あたりGDP（国内総生産）」と「1人あたり国内所得の不平等さ」を眺めてみよう!?
同じ国に住む私たち、そんな私たちが生み出したもの総額いくらになるか？＝国の中で生み出したものと交換されたおカネの量＝お値段が、それすなわちGDP(国内総生産）です。その額面が回り回って国民のお財布に入ってくるので、GDPは私たちの懐具合を指し示す指標になります（参考：「”1人あたり”GDP(国内総生産）の地球儀」で「日本の豊かさ」を考えてみよう!?）。
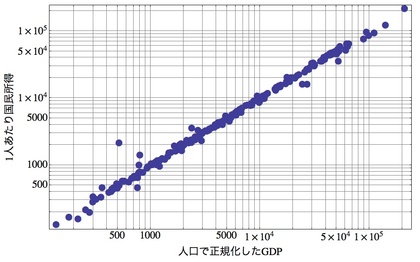
たとえば、右上のグラフは、横軸に「人口（国民数）で正規化したGDP」をとり、縦軸に「国民1人あたりの国民所得（national income）」をプロットしてみたものです。このグラフが直線的、つまり「国の中で生産されたもの価値≒国民所得」となるのは当たり前で、GDPと国民所得というものは、つまりそういう「定義」の数字なのです。
しかし、現実には、生み出すもの（の値段）や所得が誰でも同じ＝総額を人口で割ったような数値になるわけではありません。差異・違い・不平等がそこには存在しているものです。
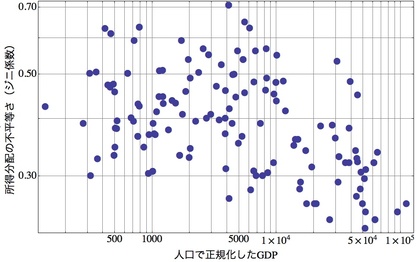右のグラフは横軸に「人口（国民数）で正規化したGDP」をとり、縦軸には「所得分配の不平等さを示すジニ係数」をプロットしてみたものです。貧しい国でも（横軸の左側）、豊かな国でも（横軸の右側）、所得分配具合には「等しくなさ」が存在することがわかります。
ジニ係数の範囲は0から1で、係数の値が0に近いほど格差が少ない状態で、1に近いほど格差が大きい状態であることを意味する。ちなみに、0のときには完全な「平等」つまり皆同じ所得を得ている状態を示す。社会騒乱多発の警戒ラインは、0.4である。
もっとも、「貧しい国でも・豊かな国でも、国民の所得分配具合は等しくない」といっても、貧しい国と豊かな国
の間での国民所得のバラツキ具合は「同じように等しくない」わけではなく、不平等さにも違いがあります。
…と、経済データを眺め・考えて続けていたならば、こんな不平等グラフはいつか姿を消すのだろうか・それともより存在感を増していくのだろうか？…とふと感じます。
」など。