2008-04-25[n年前へ]
■「"複雑極まりない"複素平面」上に「仕事」と「趣味」を描く 
複素平面"complex plane"は、複素数"complex number"の実部をx軸(実軸=real axis)・虚部をy軸(虚軸 = imaginary axis)にプロットしたものである。3+2iという複素数であればxy平面にx=3,y=2にを示す、そんな平面が複素平面だ（iは虚数単位=2乗した時に-1になる数である）。
『「仕事」と「趣味」を2次元マップで1分以内に描け』言われたら、あなたならどう描くだろう？(同世代の)"Schemeを愛するプログラマ"が描いた「趣味と仕事の関係を描いた2次元チャート」を眺め、ふと私も「仕事」と「趣味」のイメージを2次元マップに描いてみたくなった。
趣味を訊かれるといつもちょっと困る。私には趣味と仕事の違いがよくわからないからだ。
Shiro Kawai
人によって「仕事」と「趣味」というものの捉え方は違うだろうけれども、できる限り一般的に「仕事」と「趣味」という領域を2つの軸上に配置させるとしたら、どのように「仕事」と「趣味」を描くだろう？そんなことを「クイズの回答者になった気分で」描いてみたら、それは「複素平面」だった。(その人自身に対する)実利的・物質的でまさにリアルな"Real axis"と、イメージ的な「心の軸」を示す"Imaginary axis"というまさに実軸・虚軸で表現された複素平面である。
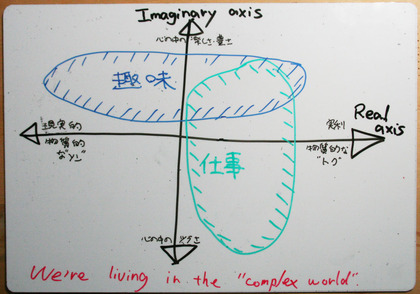
この複素平面の縦軸(の上方向)は、自分の心を豊かにする軸と捉えることができるだろう。「虚」という文字よりは、"Imaginary"という文字で捉えたい「(その人自身の)心の満足」を示す軸、である。
そして、横軸（の右方向）は、その人自身を実利的に満足させる軸である。しかし、その自分への「実利」という軸は、実は他人が何らかの形で価値を感じたことを示す軸でもあると思う。なぜなら、その「実利」は「他者が得た価値」が回りまわって流れてきたものに違いないからである。他人が得た満足が姿を変えたものであるから、である。つまり、この複素平面の横軸は「自分への実利」を示す軸であると同時に「他者を豊かにする軸」なのである。
ひとことでまとめてしまえば、この複素平面は「本人(自分)の満足」と「他人の満足」という２つの軸で形作られる平面なのだ。
'Cause we are living in a material world. You know that we are living in a material world.
Madonna "Material Girl"
その人ごとに「仕事」と「趣味」の位置づけがあると思う。どんな軸を使って、どんな風に「仕事」と「趣味」を捉えるかは、みなそれぞれ違うはずだ、と思う。「自分の中で辛さを感じながら、実利を得る仕事」もあれば（右下の象限）、「自分自身の楽しさとともに実利を得る仕事」もあるはずだ（右上の象限）。そして、さらに言うならば、同じ仕事であったとしても、その仕事がどこに位置するかは、人それぞれ異なっているだろう、と思う。そして、同じ一人の人がする同じ仕事であったとしても、きっと「その捉え方」「その座標」は変化し・移動していくものだろう、と信じている。
俳諧で「虚実」ということがしばしば論ぜられる。数学で、実数と虚数とをXとYとの軸にとって二次元の量の世界を組み立てる。虚数だけでも、実数だけでも、現わされるものはただ「線」の世界である。二つを結ぶ事によって、始めて無限な「面」の世界が広がる。
寺田寅彦 「無題六十四」
もしも、上に描いた複素平面="Complex plane"、それを言い換えれば言葉通りの「複雑極まりない世界」の上に、今のあなたが抱えているだろう「仕事」と、あなたが楽しんでいるかもしれない「趣味」は、どんなXY座標上にプロットされるだろうか。"複雑極まりない"複素平面上に、あなたはどんな軌跡を描いているだろうか。
2008-04-29[n年前へ]
■「手作り三次元グラフ」と"Life Work"
少し前に、「仕事」と「趣味」を、「本人(自分)の欲求」と「他人の満足」という2軸で表される実軸・虚軸で表現される複素平面に描いてみました。注釈を付けるまでもなく、この「仕事」も「趣味」にもカッコ（「」）が付いています。
カッコは、時に「いわゆるひとつの」という程度の意味を表したり、あるいは、時に「私の感じる言葉とは違うけれども、その人の使う言葉の定義に沿って使って・考えてみれば」というような意味合いで使われることがあります。だから、カッコ（「」）付の言葉が出てきた時には、あるいは、カッコ付の言葉とカッコが付かない言葉が同時に出てくる文章を読むときは、このカッコは何を意味しているんだろう？と考えると、その文章から何だか不思議な立体感を感じたりすることがあります。もしかしたら、それが文章の書き手の中の意識、書き手が眺めるものの距離感なのかもしれない、と感じます。
さて、「"複雑極まりない"複素平面」上に「仕事」と「趣味」を描くを書いた次の日、"Life Work"という言葉を使ったら、どのようなことを思い、どのようなものを描き・書くだろうか、と考えました。「仕事」という言葉から、"Work"という言葉を経て、"Life Work"ということを考えたらどう思うだろう？と感じました。
そして、もう一つ、「"自分(本人)の欲求・満足"と"他人の満足"という2軸で表される複素平面に、少なくとも"時間軸という軸を一つ増やしたい」とも強く思いました。私たちを大きく支配する軸でもあり、私たちにとって希少なものでもある"時間"という軸を増やしてみたいと、思ったのです。
そこで、そんな三次元空間を「ホワイトボード」と「色粘土」と「焼き鳥用の串」で作ってみました。下の写真が、その手作り”三次元空間(複素空間)”です。
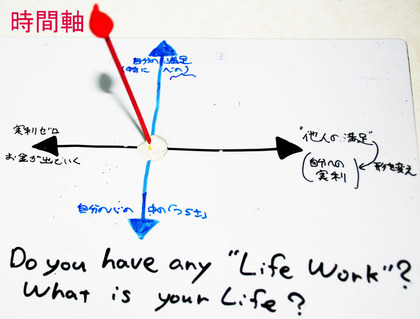
誰かが行う何かの作業を考えたとき、この空間はその誰かの作業に対する"ある3つの軸による評価値"を示したに過ぎません。他にも数限りない色々な軸があり、色々な眺め方・受け止め方があるように思います。
また、同じような作業であったとしても、その作業をする人によって、この空間での「座標」は異なってくることでしょう。それは、たとえば「梅宮辰夫の"釣り"」と「釣キチの"釣り"」が、その作業内容が同じようなのに、商品価値（黒い横軸）としては大きく違ってしまうようなことです。
試しに、今の時点での「梅宮辰夫の"釣り"」を緑色の球で、「釣キチの"釣り"」を黄色の点で手作りプロットしてみました。もちろん、材料は色粘土と焼き鳥用の串です。
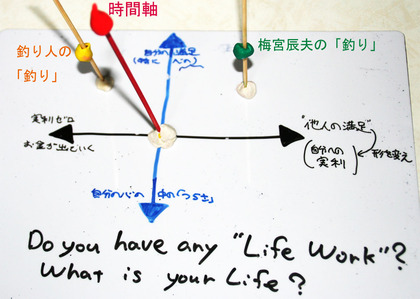
そしてまた、時間軸に沿って、誰かが行う同じ作業でも、その位置・取り扱われ方が異なってくることもあるでしょう。10年後にも「梅宮辰夫の"釣り"」が今と同じ商品価値を持っているとは限りませんし、逆に、「あなたの知り合いの釣キチの"釣り"」の方が他人に満足を与えているかもしれません。あるいは、ゴッホが生きている時点では、ゴッホの"Art Work"は収入源とはとても言えなかったわけですが、現在では、ゴッホの絵画を見るために人が集まり、その絵画を手に入れるためにたくさんのお金が集まります。
つまり、"誰かが行う何か"を示すこれらの点は、時間を経て動いていくのが普通だと思います。時代の変化にしたがって、何一つ違わない同じ"誰かが行う何か"なのに空間中を移動していって、商品価値を失ったりすることは、よくありそうに思われます。
また、その人の技術の向上といったさまざまなことを理由にして、これらの焼き鳥の串に刺さった色粘土、・・・じゃなかった、その人の作業自体が変わり、この空間における位置づけを変えていくこともよくあることだと思います。
先のことは、誰にもわかりません。「確か」でないことは、世の中に満ち溢れています。「この努力が報われる日が来るのだろうか？」「この釣り番組はいつまで続くのだろうか？」「(定年がある人であれば)定年の先には何があるんだろう」といったことをふと考えて、不安が沸いてくる人も多いことでしょう。
そんなことを考えているうちに、"小説家になりたい"という言葉に強く頷く人もいれば、"それじゃ意味がわからないよ。どんな小説を書きたいのさ？"という風に感じる人もいるだろうな、というようなことが何故か頭の中に浮かんできました。そして、さらに「"Life Work"って何だろう？」「"Life"って何だろう？」と、今更ながらに思ったのでした。
若き二ツ目が、さまざまな努力と工夫を重ねて暗中模索する姿を、私は美しいと見る。陽の当たらない場所で悪戦苦闘する二ツ目の中で、誰が将来の名手になるか。こればっかりは絶対にわからない。若くして天才ともてはやされた麒麟児が老いて駄馬になったり、ヘタクソの見本みたいだった人が五十代になって突然名人の域に飛躍したりする例が、落語家には少なくないからである。
江國滋 「落語無学」
そうそう、とりあえず一つだけ確実なことを見つけました。それは、「粘土遊びは楽しい」ということです。色鮮やかな粘土で、色んなものを作って遊ぶのは、とてもワクワクする、ということは「確か」なようです。
2008-07-18[n年前へ]
■エクセルでシミュレーション Vol.1 [静電界準備 編]
「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは（私たちのような勉強世界からの REST OF US にとっては）とても素晴らしいと思います。
ところで、現在では”表計算プログラム＝マイクロソフトのエクセル(Microsoft Excel)”だと考える人も多いことでしょう。だから、上に書いたことを言い換えれば、「エクセルでシミュレーションをする」のは、とても楽しい勉強になるということになります。
自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備（事前確認）」をしてみました。
まず、静電場を記述するポワソン方程式をテーラ級数展開することで離散化し、差分方程式に変えてみます。２次元世界を離散化するということは、エクセルの表がそうであるように「世界（画面）をセルで分割する」ということです。
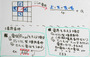
上で（x,y座標空間での）差分方程式にしたものを、さらにエクセル（表計算ソフトウェア）で解くときのやり方を図解したものが下の図です。「ある点の電位（φ）は上下左右の電位の平均にその点の(係数がかかった)空間電荷を加えたもの」になっているわけです。
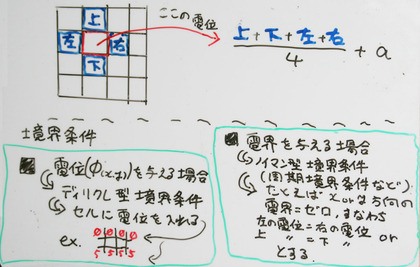
また、2種類の境界条件（電位を指定するディリクレ条件/電界を指定するノイマン条件）をどのようにエクセル上で処理するか、というのが下の部分になります。
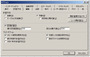
こういったセルの値が「（そのセル自身を含む）セル間の関係式」で表わされるような計算式を解くためには、エクセルの設定で「反復計算を行う」という設定を有効にしておく必要があります。エクセルのバージョンによってその設定メニュー場所は違いますが、たとえば、下の画面はExcel 2003の設定ダイアログの例です。
以上で、「静電界を記述するポワソン方程式をエクセルで計算するための前準備（事前確認）」が終わりましたから、次は実際に「身近な静電界」をエクセルでシミュレーション計算してみたいと思います。
」など。