2000-01-21[n年前へ]
■数字文字の画像学 
縦書きと横書きのバーコード
始まりはまたしても「物理の散歩道」である。
- 「新物理の散歩道」 第一集 ロゲルギスト 中央公論社
さて、その中の-横組・縦組と二つの目-という一節中の外山滋比古氏の発言が実に面白い。
「日本の漢字は横の線が発達してますから、横から読みますと目に抵抗が少なくて読みにくいですね。ヨーロッパの文字は縦の線が非常に発達していて、横に読むと非常に能率がいいわけです。数字でも縦の棒を引いて、Ⅰ、Ⅱ、Ⅲ、Ⅳ....としますが、和数字は横に線を引いて一、二、三...となります。...」という発言である。
- 文字は読む方向に対して垂直な線が多い
- また、読む方向に対して水平な線は少ない
- いずれも目のスキャン方向に対して垂直な線が多い
そこで、今回その確認と考察を行ってみることにした。サンプルとしては、外山滋比古氏の発言の通り、ローマ数字と漢字数字を用いることにする。
まずは、本来の書き方の方向に数字を並べた画像である。画像サイズは128x128である。後の処理のために、縦横比を同じにした。すなわち、本来の画像のアスペクト比とは異なる。
 |  |
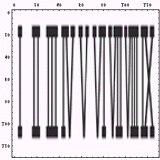この二つの画像を読む方向に目を走らせると、まるでバーコードのようである。以前、
の時に作った郵便カスタマバーコードを参考に示してみる。 |
考えてみると、バーコードは検出手段をバーコードの進行方向に走らせて、情報を読み取るわけである。人間が数字の羅列を読み取るのも、数字文字列上に目を走らせるのであるからまったくもって同じである。
一次元バーコードを考えた時、バーコードのバーは進行方向に対して垂直なものがほとんどである(若干のアジマス角を持つものもあるが)。バーコードを読み取る方向に対してのみ情報が書き込まれているのだから、それ以外の方向には等方的であるのが当然である。もし、そうでなかったらスキャン位置がちょっとずれただけでデータの読み取りができなくなってしまう。
そう考えると、先の数字文字に関する
- 読む方向に対して垂直な線が多い
- 読む方向に対して水平な線は少ない
また、本来の数字文字を並べる方向が読み書きの方向と異なる場合を以下に示す。
 |  |
さて、画像を並べるだけではつまらないので、
- 本来の書き(並べ)方
- 本来の書き方と異なる書き(並べ)方
人間の目が数字文字列上をスキャンしていくときに、選られる情報量を考えるために、読む方向に対して画像を微分したものを示す。もう少し正確に言えば、微分値の絶対値を画像にしたものである。
まずは、本来の書き(並べ)方のものを示す。
 818892 |  923836 |
微分画像の下に示した数字は微分(して絶対値)画像のピクセルの値の総和である。これをスキャン方向に対して選られる情報量の指標として扱うことにする。「スキャン方向に対して変化量が大きいということは、情報量が多い」ということだからである。
次に、本来の書き方と異なる書き方の場合を示す。
 536383 |  632338 |
それでは、「微分(して絶対値)画像のピクセルの値の総和」を比較してみることにしよう。
| 本来の書き方の場合 | 818892 | 923836 |
| 本来の書き方と異なる場合 | 536383 | 632338 |
ローマ数字、漢字数字の両方で、本来の書き方の方が(読む方向に対する)画像の変化量が大きいことがわかる。すなわち、「目のスキャン方向に対して選られる情報量」が多く、そうでない方向には冗長なのである。エラー発生率が小さくなるのである。本当にバーコードそのものである。文字はバーコードの祖先だったのである。
さて、「文字の画像学」も色々と面白そうなので、これからちょこちょこ遊んでいこうと思う。
2001-05-14[n年前へ]
2001-12-24[n年前へ]
■NHK少年ドラマシリーズのすべて
アスキー出版局。内容はとても充実してる。あの幕末未来人の主人公二人による座談会なども収録。当時、二人ともが古手川裕子に恋をしていて、その互いの恋のようすなども収録、と。懐かしすぎ。
「なぞの転校生」も好きだったが、笑ってしまうのがヒロイン香川みどりを演じた伊豆田依子が、演じたポイントとして「みどりって、わがままで、けっこう傲慢ですよね。でも、それがなくなっちゃったらみどりじゃないんだと思います。ですから、わがままさを目いっぱい出しました」 なるほどねー。（リンク）
2004-02-11[n年前へ]
■期待に添える範囲で
そういえば、先週だったかラジオの番組のインタビューを受けた。が、いつものことだが、「こんなヤツのハズだ」という期待に添えているかどうかを考えると、逃げ出したくなる。いつだったか、ワイドショーのスタッフから電話がかかってきたときも、凄かった。あぁ、きっと私の部屋はビデオやPCでイッパイと思われてるんだろうな、と思うような感じだった。
凄いと言えば、何年も前に工学社の「おもしろ実験サイトオールガイド」という本のための座談会に出た時も凄かった。(休出から直行で)「西武池袋駅前で集合」という、これも何ともイヤンな待ち合わせ方法だったが、「-西武池袋駅前-だなんてそんな大雑把な待ち合わせ方法で本当に落ち合えるのだろうか？」なんて当然起きる疑問も大間違いだったことがその場に行ってすぐ判った。「あぁ、今日のメンツはこの人達だろうな。いや、絶対この人達に違いないよなぁ」と断言できるような人達が集まっていたからだ。そして、「私もこの中の一人なんだなぁ…なじんでないよなぁ、いやそれともなじんでいるのかなぁ…うーん、一体どちらが良いのかなぁ…？」と考えだすと、これまた何ともイヤンな気持ちになったのだった（その気持ちは談話室「滝沢」の入り口でイラスト用の顔写真を撮られる段でピークを迎えたのだけれど）。
まぁ、期待に添える範囲で適当に。「よっぽどおっぱいが好きな人なんだろう(by れいこさん@はてな)」と会う前には思われ、知り合った後には「とてもおだやかな雰囲気を持つ大人の人」に印象が変わってしまった私だけれども、期待に添える範囲で適当に…。ということで、次のできるかな?は「帰ってきたオッパイ星人の力学 アダルトビデオ鑑賞 編(仮題)」だぁ。ワイン飲みながら、動画ブロックマッチングソフトも作ったし、サンプルビデオも落としてきたし、科学の力で「オッパイ星人の力学 アダルトビデオ鑑賞三昧!? 編(仮題)」だぁ。（本当に、おだやかな雰囲気を持つ大人の人…？）
2011-05-21[n年前へ]
■面白い企画が詰まった「恋と童貞 ２号」
再開された六角橋商店街の闇市に遊びに行ってみると、手作り感満載のミニコミ誌を並べ売っている人たちがいました。そこで何冊か買った内の一冊が、その名も「恋と童貞 ２号」というもので、たとえば、自分の中の理想の乙女像を互いにプレゼンし合う（そしてツッコミあう）「超バトルロイヤル 俺の乙女選手権」や、夢の座談会「決戦!! 我らが夢の おっぱいVSおしり」、あるいは、ヘテロやホモや色んな相互関係を数式モデル化し議論する論文「童貞喪失機会問題に関する試論」といった話が詰まっていて、とても楽しめる一冊でした。
「童貞喪失機会問題に関する試論」の内容を私の解釈で書いてみると、「（人の）魅力」が次のような式で書けるとして、
「魅力」=「伝達力」×「出会う人の数」＋「見た目・財力など」
その「伝達力」を「本人が決めるもの」「周囲が決めるもの」という２種に分けてみれば、それらの値域次第で「童貞喪失機会」の確率が決まることがわかる（かもしれない）、というものでした。
「…このモデルのこの部分には改良の余地がある」といったことを感じたりもするのですが、そんなことを読者たちが考え出し始めてしまうこと自体が、「恋と童貞」の作り手たちの狙いなのかもしれません。
「俺の乙女選手権」「おっぱいVSおしり決戦!!」…読み進むうちに私たちの中にある深層心理も考えさせられたりして…「恋と童貞 ２号」面白いです。
」など。