1999-12-21[n年前へ]
■恋の力学 
恋の無限摂動
クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。
「できるかな?」では以前、
において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。
といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。
今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。
恋する二人の間に働く力をもう少し正確に記述しておくと、
- 「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「恋の力」=優柔不断度 * 「恋の加速度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。
また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。
さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。
初期状態は
- 「男」位置=5, 速度=0,魅力=100,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
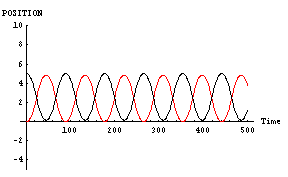 |
「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。
この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。
その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、
- 「男」位置=5, 速度=0,魅力=10,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
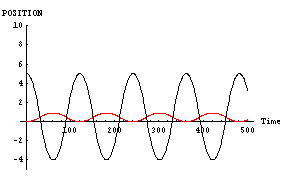 |
「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。
先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。
それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、
- 「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=1000,優柔不断度=10
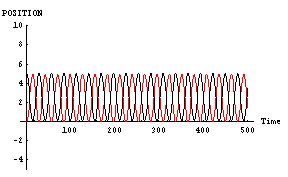 |
「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。
最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、
- 「男」位置=5, 速度=0,魅力=2,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=2,優柔不断度=10
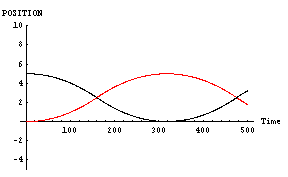 |
これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、
- 「男」位置=5, 速度=0,魅力=0,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=0,優柔不断度=10
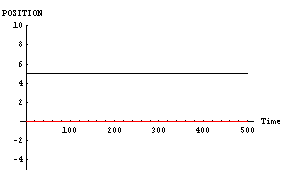 |
これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。
さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。
さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。
そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか?果たして、未来の行動パターンは予測可能なのだろうか?色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか?
それらは次回の課題にしておく。題して、「恋の力学 三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
2000-01-21[n年前へ]
■数字文字の画像学 
縦書きと横書きのバーコード
始まりはまたしても「物理の散歩道」である。
- 「新物理の散歩道」 第一集 ロゲルギスト 中央公論社
さて、その中の-横組・縦組と二つの目-という一節中の外山滋比古氏の発言が実に面白い。
「日本の漢字は横の線が発達してますから、横から読みますと目に抵抗が少なくて読みにくいですね。ヨーロッパの文字は縦の線が非常に発達していて、横に読むと非常に能率がいいわけです。数字でも縦の棒を引いて、Ⅰ、Ⅱ、Ⅲ、Ⅳ....としますが、和数字は横に線を引いて一、二、三...となります。...」という発言である。
- 文字は読む方向に対して垂直な線が多い
- また、読む方向に対して水平な線は少ない
- いずれも目のスキャン方向に対して垂直な線が多い
そこで、今回その確認と考察を行ってみることにした。サンプルとしては、外山滋比古氏の発言の通り、ローマ数字と漢字数字を用いることにする。
まずは、本来の書き方の方向に数字を並べた画像である。画像サイズは128x128である。後の処理のために、縦横比を同じにした。すなわち、本来の画像のアスペクト比とは異なる。
 |  |
この二つの画像を読む方向に目を走らせると、まるでバーコードのようである。以前、
の時に作った郵便カスタマバーコードを参考に示してみる。考えてみると、バーコードは検出手段をバーコードの進行方向に走らせて、情報を読み取るわけである。人間が数字の羅列を読み取るのも、数字文字列上に目を走らせるのであるからまったくもって同じである。
一次元バーコードを考えた時、バーコードのバーは進行方向に対して垂直なものがほとんどである(若干のアジマス角を持つものもあるが)。バーコードを読み取る方向に対してのみ情報が書き込まれているのだから、それ以外の方向には等方的であるのが当然である。もし、そうでなかったらスキャン位置がちょっとずれただけでデータの読み取りができなくなってしまう。
そう考えると、先の数字文字に関する
- 読む方向に対して垂直な線が多い
- 読む方向に対して水平な線は少ない
また、本来の数字文字を並べる方向が読み書きの方向と異なる場合を以下に示す。
 |  |
さて、画像を並べるだけではつまらないので、
- 本来の書き(並べ)方
- 本来の書き方と異なる書き(並べ)方
人間の目が数字文字列上をスキャンしていくときに、選られる情報量を考えるために、読む方向に対して画像を微分したものを示す。もう少し正確に言えば、微分値の絶対値を画像にしたものである。
まずは、本来の書き(並べ)方のものを示す。
 818892 |  923836 |
微分画像の下に示した数字は微分(して絶対値)画像のピクセルの値の総和である。これをスキャン方向に対して選られる情報量の指標として扱うことにする。「スキャン方向に対して変化量が大きいということは、情報量が多い」ということだからである。
次に、本来の書き方と異なる書き方の場合を示す。
 536383 |  632338 |
それでは、「微分(して絶対値)画像のピクセルの値の総和」を比較してみることにしよう。
| 本来の書き方の場合 | 818892 | 923836 |
| 本来の書き方と異なる場合 | 536383 | 632338 |
ローマ数字、漢字数字の両方で、本来の書き方の方が(読む方向に対する)画像の変化量が大きいことがわかる。すなわち、「目のスキャン方向に対して選られる情報量」が多く、そうでない方向には冗長なのである。エラー発生率が小さくなるのである。本当にバーコードそのものである。文字はバーコードの祖先だったのである。
さて、「文字の画像学」も色々と面白そうなので、これからちょこちょこ遊んでいこうと思う。
2003-02-02[n年前へ]
■モーニング娘。でクラスタ分析 
グラフ理論で今日からあなたもプロデューサー
昔からワタシには「手を抜くために色々とクダラナイことをする」という悪い癖がある。しかも、そのクダラナイことをした結果、必ずと言っていいほどに結局のところ苦労が増えまくるという結果になるのである。いわば、ドラえもんの「のび太」がいつもドラえもんの便利な道具に頼り、しかもその道具にしっぺ返しを必ず受けてしまうのを地でいくタイプなのであった。いつも、ワタシは手を抜くための道具を色々と作り、そして必ずそのしっぺ返しを食っていたのである。いわば、ドラえもんののび太とドラえもんを一人二役でマッチポンプのように演じ続けてきたのがワタシのこれまでの人生だったのである。
最初に記憶に残っているそんなワタシの悪い癖は小学生の頃のことだ。生徒会か何かでワタシは募金の集計をしなければならなかったのである。1000人を遙かに超える生徒がせっせと集めた募金なのだから、硬貨にしても膨大な枚数だった。といっても、ほとんどは一円玉とか10円玉だったのだから、それほどの金額ではなかったのだろうけれど、とにかく膨大な枚数だったのである。
そこで、ワタシは「ここは硬貨の重さを量って、金額を計算してみるのはどうだろうか?」と提案してみたのである。各硬貨の一枚当たりの重さは判っているわけだし、各硬貨に分けた上で全部の重さを量ってそれで金額に換算しちゃえば楽じゃないの、と提案してみたのである。ゼニ勘定に疲れていた周りの人々もその提案に喜び、「重さの誤差はどのくらいあると思う?」などとガヤガヤと計算しながら、みんなでせっせと硬貨を袋に入れて重さを計り始めたのである。
そして、机の上に重さを量り終わった硬貨の袋が何袋も並ぶ頃、そんな小さな銀行泥棒たちが盗んだお金を袋に入れてる最中のような様子を小学校の先生が発見してしまったのである。そして、当然のごとく私たちは先生にこっぴどく怒られたのである。「みんなが苦労して集めたお金のありがたさが判っていない」と当然のおしかりを強く強~く受けたわけである。「算数の問題解いてるんじゃぁないんだから!」とこっぴどく怒られたわけなのである。結局、私たちは硬貨の袋から硬貨を取り出して一枚一枚数え直すことになったのであった。もちろん、他の人をそそのかしたワタシに対する周りの視線は非常にキツく、ワタシの疲れも倍増したのであった。最初から硬貨の数を数えた方がよっぽど楽だったのである。
大人になってしまったワタシは今だにそんな「手を抜くための道具」を作り、そしてしっぺ返しを食らい続けている。三つ子の魂百まで、というわけなのであるが、今回は少し前にやってしまったそんな失敗を反省を含めて書いておこうと思う。
ワタシは仕事の上で色々な調査をしなければならないことがある。例えば、他のライバル会社がどんなことをしているかとか、あるいは、もっと詳しくライバル会社の中の人たちがどんな風に繋がっているか、とかを調べなければならなかったりすることがある。色々な発表資料を読んだり膨大な数の特許を読んだりして、そこに登場してくる人たちの関係を調べて、色々な推定をしていかなければならない。そのためには、たくさんの書類を調べなければならないわけで結構これがシンドイ作業なのである。
で、ワタシはこう考えたのだった。数百件もあるいは数千件も色々なものを読んで、その中に登場する人たちの関係を推定するなんてツライから、「たくさんの文書を勝手に読んで、勝手にその文章からライバル会社の中の人の関係を推定するソフト」を作っちゃえ~、と思ったのである。手を抜くためのクダラナイことのためには、苦労をいとわないワタシはそんなゴリゴリゴリゴリ真面目にそんなソフトを作ったのであった。「たくさんの文章の作者を調べ、その共著の関係から著者間の関係を調べる」というそんなソフトをせっせと作ってみたのである。そして作った後は、もちろんソフトのテストをしてみよう~、ということになった。
じゃぁ、そのサンプルデータは何を使ってみようかなと考えている時に、頭の中のどこかでモーニング娘。の「ここにいるぜぇ!」が流れ始めたのである。そこで、ワタシはモーニング娘。を含むハロープロジェクトを他社に見立てて、これまでに発売されたCDに参加している頻度・関係性等から、ハロープロジェクト内の「それぞれの人の配置」を調べてみることにしたのであった。
というわけで、つんく率いるハロープロジェクト関連で発売されているCDの枚数(なんと80枚以上だ!)に驚きながらも、CDに参加しているメンバーのデータをソフトに流し込んで、適当な各メンバーの関連性を示す数値を計算した上で、まずは各メンバーを近いものに分けるために、クラスタ分析してみた。ここで、解析ソフトは各CDに誰が参加しているかだけを知っていて、「モーニング娘。」とか「タンポポ」とかのグループが結成されていることは知らないのであるが、とにかくハロープロジェクトの中の各メンバーの「組織図」が判るわけだ。(ちなみに、ここでは似通ったものを樹形図(似通った度合いを示すグラフ、会社で言えば組織図みたいなもの)として表示するために、「Excelアドイン工房」のクラスタ分析アドインを使っている。)
まずは、前半41作のCDから推定したハロープロジェクトの中の各メンバーの関係性を示したのが下のグラフである。
 |
この樹形図グラフを眺めれば、(CDのカップリングから判断される)で誰と誰が結構近い関係にあるか、というようなことが判るハズである。といっても、このグラフでは色々なメンバーが参加したアルバムもあるいは一つのグループだけが歌うシングルも同じ重みで計算していたりするので、モーニング娘。あたりのファンの感覚からは大きくずれるかもしれないけれど、とにかくこんな「組織図」が計算されるのである。
上の前半41作から計算した樹形図の方は結構シンプルなものなのだけれど、次に示す後半41作のCDから推定した後半41作のCDから推定した各メンバーの関係性の方はもう少し複雑だ。組織的にライバル会社ハロープロジェクトは前半より複雑になってきているのである。
 |
こんな感じで、他社(ここではハロープロジェクトをそれに見立てたが)の発表資料(特許とか製品報告とか)からこんな各メンバーの組織図を示す解析ソフトを作ってみたわけなのだけれど、これではどうも不十分なのである。どうしてかといえば、各メンバーの結びつきがこの樹形図ではどうしても判りにくいのである。こんな風に各メンバーが一次元に並んでいる図ではどうも今ひとつ判らないことも多いのである。そこで、ワタシはさらに「各メンバーの結びつきを示す二次元グラフ」を出力することにしたのである。誰と誰がどのくらい近い関係にあるかなどを判りやすく表示させてみたのだった。そんなサンプルを少ないデータで表示させてみたのが下のグラフだ。モーニング娘。のメンバーの関係が判りやすい?グラフになっているのが判ると思う。
このグラフ上で各メンバーを動かせば、「飯田をこっちへ持っていけばどうなる?あー、安部がそっちへ行っちゃったよー。どうするー?」というような具合で、各メンバーの配置やプロジェクトのメンバー編成などを実験することができるのである。グラフ理論で今日からあなたもプロデューサーなのである。グラフぐりぐりで、今日からあなたもつんくなのである。グラフ配置で誰でもつんくの気持ちになれるのである。
という感じで、ソフトのテスト(になっていたのだろうか?)を終えたワタシはライバル会社の組織図を作ったのである。で、それを使いながら「この人たちはきっとこんな感じの組織になっているんですよー。そして、こんな感じでその組織は変化していったんですよー」なんて報告をしたのである。すると「おぉー、これは結構使えるかもー、なかなかスゴイぞー」となかなかに良い反応だったのである。
そこで、さらにワタシは調子に乗って「ライバル会社の各メンバーの結びつきを示す二次元配置グラフ」の方で「この人をこっちに近づけるとこの人がこっちへー、これがライバル会社の人間関係なんですよー、ほらほら~」と見せたりすると、もうこれが「おぉぅ…? …これは何て言ったら良いのかなぁ…?スゴイ…んだけどなぁ……」と逆効果どころじゃなくもう引きまくりだったのである。そして、引いてしまった引き潮をもうどうにもすることもできないままに、結局そのグラフはお蔵入りしてしまったのであった。結局のところ当たり前のようにワタシはたくさんの書類をせっせと読まなければならなくなったのである。いつものように、手を抜くために色々とクダラナイことをして、結局のところ作業量は全然減らなかったのである。昔の小さな銀行泥棒の根性は全然直っていなかったのである。のび太とドラえもんの一人二役マッチポンプ人生はまだまだ終えられそうにないのが、ちょっと哀しい今日この頃、なのである。
2003-03-23[n年前へ]
■今日見た景色 
「写真の極点がポルノグラフィと戦争報道であるとするなら、すべての写真はいかに抵抗しようとしてもそれらの二極間のいずれかに位置するだろう」「バグダッドの官邸から立ち昇るボリューメトリックな爆煙も、風に舞うコンビニ袋も、少女の性器も、高速道路の植え込みの萎れた花々も、すべて撮られたものは等価であると思いたいし、そういった写真を撮りたい」
私もそんな一次元の曲線の上で「今日見た景色」を眺め続けて行こうかな、と。