1998-11-20[n年前へ]
■モアレはデバイスに依存するか? 
まず、以下のような2つの同心円画像をつくる。(なお、このような画像を簡単に作るために、Photoshop用のフィルターを作った。詳しくは「Photoshopの同心円フィルターを作る。」を参照して頂きたい。)以下の2つの画像は少し中心位置がずれている。また白く見えるところは255の値を持ち、黒く見えるところは0の値を持っている。(画像自体は512x512であり、表示の際に128x128に変換している。だから、この画像をそのまま保存して頂ければ、512x512のサイズで保存することができる。)
 |
 |
- 黒(0)+黒(0)=0(すなわち黒)
- 白(255)+白(255)=255(すなわち白)
- 黒(0)+白(255)=255(すなわち白)
- 画像1を白黒反転し、画像1'を作る。
- 画像2を白黒反転、画像2'を作る。
- 画像1'と画像2'を加算し、画像3を作成する。
- 画像3を白黒反転し、画像3'を作成する。
 |
それでは、以上の画像変換を小さい画像でまとめて表示してみる。
 |  |  |
ところで、上の3つの画像をそれぞれ平滑化してみる。すると、以下のようになる。
 |  |  |
以下でもう少し詳しく考えてみる。
重ね合わせにおける加算演算
下のような画像A、画像Bを考える。拡大してあるが、画像自体は1x2ピクセルのサイズである。また、白=255、黒=0とすれば、いずれも平均値は128程度である。 |  |
- 黒+黒=黒
- 白+白=白
- 黒+白=黒
 |  |  |
 |  |  |
 |  |  |
これに平均値も示すと以下のようになる。ここでは、LBPなどの紙に出力する際によく使われる、白=0、黒=255という表記をする。
 |  |  |
 |  |  |
 |  |  |
同じ128+128でも、結果は128になるか256になるかの2種類ある。同じもの同士であれば、結果は128であるし、そうでなければ256になる。そのために、平均値が保存されないのである。このように、平均値が保存されない、言い換えれば、加算演算の結果が線形でない場合にはモアレが発生することになる。もしも、マクロに見て「128+128=256」が多い領域があれば、それはモアレの黒い部分であり、そうでない所は比較的明るい部分であるということになる。
ロゲルギストの-モアレが生じる理由は黒さの非線形性による-という言葉はこの「128+128=128、と128+128=256という結果の違いがあり、それがモアレの原因である」ということを示している。
それでは、そのような現象「128+128=128という非線形性」が起きない状態を作ってみる。それには加算の結果である黒がサチらないようにすれば良い。
 |  |  |
 |  |  |
 |  |  |
これでは、いずれの状態でもグレー+グレー=黒、すなわち、64+64=128という風になっている。これは黒がサチっていないからである。すなわち、-モアレが生じる理由である黒さの非線形性さ-がない状態になっている。
それでは、この状態で計算実験Aと同じことをしてみる。それを計算実験Bとする。念のため、計算実験Aをもう一度示す。
 |  |  |
 |  |  |
 |  |  |
| 画像1の黒=0を128にした画像4を平滑化したもの | 画像2の黒=0を128にした画像5を平滑化したもの | 画像4,5を加算したもの |
モアレができていないのがわかるだろうか。これはグレー(128)+グレー(128)=256(もっと黒)で線形な関係が成り立っているからである。平均化された画像で濃度がどこも倍近くになっているのがわかると思う。
モアレのデバイス依存性
LBPではトナーが有る所、すなわち、画像が有る所はほぼ完全に影になる。例え、2枚重ねてもやはり影のままである。しかし、インクジェットならどうだろうか。OHPで使うと、黒といってもLBPに比べて薄い。1枚のOHPの黒よりも、2枚のOHPの黒を重ねた方がかなり黒い。ということは、「黒+黒=もっと黒」と同じである。したがって、OHPを重ね合わせても濃度が保存されている。すなわち、モアレが比較的に出来にくいことになる。ということは、OHPを何で作るかによってモアレの具合が変わることになる。付け加えれば、実際のOHPの場合には透過率を考えなければならない。透過率というものは単なる重ね合わせでない、具体的に言えば、加算演算でなく乗算演算である。それでも、話としては大体は同じことである。
今回はOHPの話に絞ったが、透過原稿でなく反射原稿についても同じである。むしろ、反射原稿の方が乗算演算でなく、加算演算である分、今回の話そのままである。したがって、一般的なモアレについてインク(もしくはそれに相当するもの)の加算演算の具合によって、モアレの発生具合が違うと考えられる。
また、話の単純のために白黒の話に限ったが、カラーのモアレなどについてもほぼ同じであろう。トナーとインク、また、混ざりやすいものと混ざりにくい物の違いなどでも面白い結果が出そうである。TVや液晶のようにほぼ線形の重ね合わせが成り立つであろうものと比較するのも面白そうである。
今回の話を考えている途中で、OHPの重ね合わせと干渉の共通点については、結構奥が深いような気がしてきた。そのため、別の回でもう少し詳しく考えたい。
1999-01-28[n年前へ]
■Photohoの落とし穴 
ノイズフィルタに要注意
Phtoshopは大変巨大なソフトである。巨大すぎてよくわからないところも多い。巨大な割にはマニュアルは薄い。性能の割には安いと思うのだが、もう少し詳しいマニュアルも作って欲しい。Adobe(アドビでなくて)からなら入手できるのだろうが。
今回はPhotoshopの「ノイズフィルタ」について考えてみたい。 ノスタルジックにしたい時など重宝するフィルタである。
 |
 |
まず、「均等に分布」のノイズを見てみる。
 |
 |
 |  |
両方とも、「ノイズの量」を55にしてある。左上の「均等に分布」の画像を見ると200から255までの間にノイズが-均等に分布-していることがわかる。ということは255 から ( 255-「ノイズの量」 ) までのレベルにノイズが-均等に-分布していることがわかる。ただし、「ノイズの量」の最大値は999であるから、さらに、何らかの処理が加えられているのだろう。
同じように、「ガウス分布」の方もガウス分布の分散、中心値、ノイズ量を「ノイズの量」の数値に従い適当に導いているのだろう。大雑把にはわかった。
今回は濃度の分布に対する考察はここまでにしておく。次は位置分布である。今回のメインはこちらである。
まずは、下の図.3の拡大図を見て欲しい。
 |
そこで、Photoshopのノイズフィルタの位置分布に何らかの周期性があるのかどうかを調べてみたい。
そこで、それぞれのノイズ画像をフーリエ変換し周波数領域に変換する。
 |  |
すると、縦線が見える。つまり、どちらも横方向に周期性があることがわかる。またそれよりレベルは小さいが縦方向にも周期性がある。それぞれの分布で周期性は異なっている。
横方向で一番レベルが大きいものは周期128ピクセルである。これはどちらの分布に関しても言えそうである。128とはいかにも納得できる数字である。
縦方向は85ピクセル位か?100位のもあるな? いずれ、より詳しい解析を行ってみたい。
さて、以前PhotoShopの乱数Pluginを作ろう。----FilterFactory編---(1999.01.08)で作成したプラグインはこんな周期性を持っていないことを保証しておく。以下がその証拠である。
 |  |
今回の結論:Photoshopのノイズフィルタには要注意である。
今回の教訓:何はともあれ疑ってかかれ。
1999-04-10[n年前へ]
■シリアルデータをExelへ転送したい 
計測器のデータを簡単に入力しよう
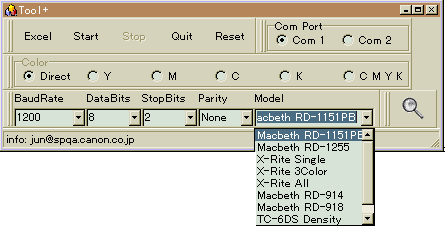
計測を行って、解析処理を行いたい時にどうにも入力が面倒なことが多い。処理はExcelなどで行うことが多いのだが、計測したら即座にExcelのワークシートに入力されたら便利である。膨大なデータを計測して、そのデータからどれだけ意味ある情報を抽出することが簡単にできたらいい。そう考えて、シリアルデータ出力を持つ計測器の出力データをExcelへ自動的に送信するソフトを作成した。現在、対応しているソフトは画像関係の計測器の6種類だ。 Tool++はシリアル出力を行うことができる計測器のデータをExcelのシートへ自動入力するソフトウェア。計測すると同時にデータがExcelのシートに取り込まれる。画像出力結果のデータ処理などを簡単に行うことが出来る。
現在、対応している計測器は
- Macbeth社製 RD-1151PB 濃度計
- Macbeth社製 RD-1255 濃度計
- Macbeth社製 RD-914 濃度計
- Macbeth社製 RD-918 濃度計
- X-Rite社製 X-Rite404 濃度計
- 東京電色 かぶり測定器 TC-6DS(I/Fをつくる必要がある。といってもとても簡単なものだ)
ソフトのダウンロード
Tool++の画面
さて、本家「できるかな」のゴン太くんにならい、本サイトでもサブキャラを登場させることにした。称して「ちび太」くんである。今回は、ちび太はせっせと計測しているところだ。MacromediaFlashをいじってみたかったので、Flashのプラグインをインストールしていない人は見えないだろう。内容は大したしたものではない。
計測すると、データはExcelへ自動入力される
1999-09-05[n年前へ]
■ACIIアートの秘密 
画像をASCII文字に変換するソフトを作ろう
ASCII文字で描かれたモナリザを初めて見たのは、まだ大型コンピューターしかなかった頃だ。当時、記憶媒体の紙テープをパンチした紙くずと、ラインプリンタから出力されたASCIIアートで遊んでいた。
今回ASCIIアートを用いていくつか実験をしてみたかったので、画像をASCII文字に変換するソフトウェアを探してみた。例えば、
- 清竹's テキスト絵 HPリンク集 (http://www2.nkansai.ne.jp/users/kiyo/ )
子どもである作成したソフトウェアは以下だ。もちろん、フリーウェアだ。ただし、いつものごとくアルファ版の中のアルファ版なので、再配布は禁止である。ここからいくらでもダウンロードできるので、構わないだろう。
さて、このソフトウェアは画像をASCII文字に変換して表示・保存することができる。変換の仕方は、- 白背景に黒文字
- 黒背景に白文字
- 白背景に色文字
- 黒背景に色文字
- Windows Bitmap形式
- Text形式
- Html形式
画像を読みこむには標準ではWindowsBitmapのみであるが、Susieプラグインを用いれば、色々な画像形式に対応することができる。
使用手順は以下の通りだ。
- image2asciiを起動する。
- OpenFileボタンを押して、画像を読みこむ。
- Fontボタンを押して、フォントを選択する。(このソフトは使用するフォントの濃度カーブを計測し、正確な画像再現を狙うのだ!!)
- 画像変換モードを選択する。
- ImageToAsciiボタンを押して、変換を行う。
- 必要であれば、SaveFileボタンから適当な形式で保存を行う。
動作画面例は、例えば以下のようなものだ。
 |
 |
 |
 |
Text形式で保存した場合のサンプルはこんな感じだ
Html形式で保存した場合のサンプルも示しておく。白黒文字への変換モードであればテキスト形式で保存するのが良いと思う。白黒文字の場合にスペースが変換画像中に含まれていると、画像ずれが生じてしまうからだ。これも簡単に直せるのであるが、直すのは次回にしておく。慣れないプログラミングを一気にしたせいで疲れてしまったのだ。もしすぐに使いたい方は、エディターで適当に置換すれば良いと思う。 さてさて、このプログラムを作成した理由は、これを用いて実験を多々行ってみたいからなのである。キーワードは、デバイス、ガンマ、安定性、逆問題、色空間...である。というわけで、続きは次回に...
1999-09-08[n年前へ]
■続ACIIアートの秘密 
階調変換 その1
さて、今回は
の続きである。今回はASCIIアートの階調変換に関する話である。原画像からASCII文字画像に変換するときにどう変換するか、という話の第一話である。 まずは、白から黒までの256階調の基準チャートとASCII文字によるチャートを示してみよう。
両者ともかなり縮小表示している。従って、ASCII文字チャートの方は文字がつぶれて滑らかに見えている。一見すると、ASCII文字チャートの方は白地に黒い文字を印字しているため、完全に黒いようなものは出力できない。そのため、全体的に白く見える。
これらの2つの画像のヒストグラムを示してみよう。ばらつきが多少あるが、256階調の基準チャート(上)では256階調にわたって存在している。しかし、ASCII文字チャート(下)では(ざっと見た限りでは)35階調程度しか存在していない(これは使用するフォントによって異なる)。もともと、ASCII文字は数多くあるわけではないし、平均濃度が等しい文字も存在するので、この程度になってしまうのはしょうがない。また、最も黒い領域でも、256階調の基準チャート(上)の半分程度の濃度しかない(これも使用するフォントによって異なる)。
ところどころに「使用するフォントによって異なる」という注釈を入れいるがこれが前回作成したimage2asciiの特徴である。指定のフォントを用いて画像出力を行った結果を用いてガンマテーブルを再構成するのである。逆にいえば、その指定のフォントを用いない場合には意図した画像は得られないわけである。「DeviceDepend」な技術というわけである。
 |
 |
そもそも、オリジナルの画像から、この程度の階調しかないASCII文字画像へどのように変換したら良いだろうか? 先に基準チャート(上)とASCII文字チャートの例を示したが、そもそもそのASCII文字チャートはどのようにして変換するのだろうか?
まず思いつくのはオリジナル画像の濃度に一番近い濃度の出力を行う方法である。それを濃度精度重視の変換と呼ぼう。そして、もうひとつは、オリジナル画像の中での相対濃度を基準とする変換である。すなわち、オリジナルの最大濃度をASCII文字出力による最大画像に合わせ、オリジナルの最小濃度をASCII文字出力による最小画像に合わせ、あとは単に線形に変換する方法である。こちらを(まずは単純な)階調性重視の変換と呼ぼう。その変換の構造を以下に示してみる。
 |  |
濃度精度重視の変換(左)では、ある濃度以上になると全て同じ濃度で示されてしまう。階調性重視の変換(右)ではそんなことは生じない。しかし、オリジナルの画像と変換後の画像の濃度はかなり異なってしまう。これら2つのやり方によるASCII文字チャートをそれぞれ示してみる。
濃度精度重視によるASCII文字チャートと階調性重視によるASCII文字チャート(下)のどちらが自然だろうか?濃度精度重視によるASCII文字チャートは階調の中程までは基準チャート(上)と非常に近い濃度を保っている。そのかわり、それ以降の濃度が高い部分はまったく階調性を失っている。少なくともこの基準チャート(上)のように256階調にわたり均等に濃度が存在するような画像を扱うのであれば、階調性重視によるASCII文字チャート(下)の方が自然だろう。というわけで、前回作成したimage2asciiは階調性重視による変換を用いている。
さて、今回は256階調全てにわたって滑らかな基準チャートを用いて考えてみた。しかし、実際の写真はそんなものではない。色々な濃度が均等に現れるわけではないし、そもそも狭い濃度領域しかない画像の場合もあるそういった場合には、数多くの問題が生じる。また、単に(単純な)階調性重視によるASCII文字チャート(下)が優れているわけでもなくなる。場合によって何が優れているかは異なるのだ。一般的な画像において、一体どんな問題が生じるのか、ということを次回に考えてみることにする。そして、新たに2種類の変換方法を加えてバージョンアップしたimage2asciiの登場するわけである。
今回は、その3つの変換方法の違いにより出力画像にどのような違いが生じるかを示すだけにしておく。先入観が無い状態で、優劣を判断してみると良いと思う。次の例は人物写真である。まずは、オリジナルの写真である。
 |
以下にimage2asciiを用いて変換したものを示す。
 |  |  |
これらの違いがどのようなものであるかを次回に考える。